Действия над комплексными числами.

Если два комплексных числа складывать, перемножать или делить друг на друга, то мы получим новое комплексное число.

Пример 1. Дано z  = -1 + 2i, z  = 3 - 5i. Найти z  + z . Решение z  + z = -1 + 2 i + 3 - 5i = 2 - 3i, т.е. складываются вещественные части и мнимые части.

Пример 2 Дано z  = 2 + 3i, z  = -1 + i. Найти z  - z . Решение z  - z = 2 + 3 i –(-1 + i) = 2 + 3i + 1 – i = 3 + 2i. т.е. складываются вещественные части и мнимые части.

Пример 3 Дано z  = -1 + 2i, z  = 3 - 5i. Найти z * z . Решение, z * z = (-1 + 2 i)*(3 - 5i) = -3 + 6i +5i – 10 i² = - 3 +10 +11 i = 7+ 11 i, надо помнить, что i² = - 1.

Пример 4 Дано z = 2 - i,,   = 2 + i. Найти z * .

Решение z *  = (2 – i) *(2+ i) = 2² - i² = 4+1 = 5, где i² = -1. Произведение комплексно сопряженных чисел есть вещественное число равное сумме квадратов вещественной и мнимой частей.

Например, 1) z = 1 + i,  = 1 – i, z * =1² + 1²=2

            2) z = 3 + 5i,  = 3 - 5i,, z * =9 + 25=34

Пример 5 Дано z  = -1 + i, z  = 2 - 3i. Найти z = (1 + i)/(2 - 3i). Решение z = (1 + i)/(2 - 3i) = (1+ i)(2 +3i) / (2 – 3i)(2+3i) = (2 +2i +3i +3i²)/ (4+9) = (2 – 3 + 5i)/13 =

 = -1/3 + (5/13)i. Чтобы выделить вещественную и мнимую часть числа z надо числитель и знаменатель дроби умножить на число сопряженное знаменателю.

Рассмотрим еще один подобный пример.

Произвести действие, выделить вещественную и мнимую части числа

(2 + i)/(1 + 2i).

Решение. (2 + i)/(1 + 2i) = (2+ i)(1 -2i) / (1 + 2i)(1 - 2i) = (2 +i - 4i - 2i²)/ (1 +4) = (2 + 2 - 3i)/5 = (4 - 3i)/5= 4/5 - (3/5)i.

Геометрическое изображение комплексного числа z = x + iy.

у

Выберем декартову прямоугольную систему координат. По оси абцисс отложим вещественную часть числа х, по оси ординат отложим мнимую часть числа у, получим на плоскости точку z с координатами (х,у)

							Рис.1
							х

 

 

х

                     0

Рис.1

Ось ох называется вещественной осью

Ось оу называется мнимой осью.

Вся плоскость хоу называется плоскостью комплексного переменного.

y

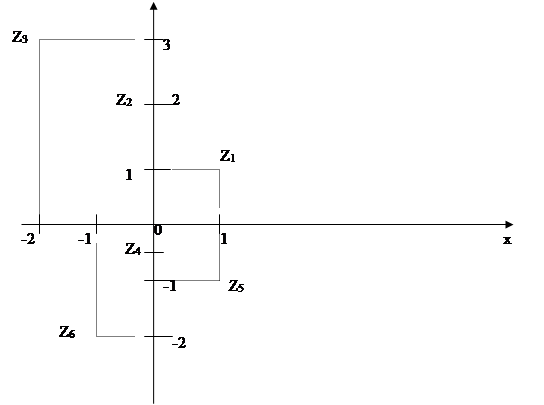
Пример. Построить числа z  =1+ i; z  =2 i, z  = -2+3 i; z  = -1/2 i, z  =1 - i, z  =-1-2 i Рис2.

 

 

 Тема 4. Аналитическая геометрия. Координатный метод. Прямая линия на плоскости.

Аналитическая геометрия - область математики, занимающаяся изучением геометрических задач методом координат. Основная идея аналитической геометрии проста: положение точки на плоскости можно описать двумя числами и, таким образом, перевести любое утверждение о точках в утверждение о числах. Основоположниками метода координат принято считать Рене Декарта (1596-1650) и Пьера Ферма (1601-1665).

Декартова прямоугольная система координат на плоскости задается так: выбираются две взаимоперпендикулярные прямые с выбранным положительным направлением на каждой прямой - оси координат, точка пересечения прямых – начало координат. Выбирается на осях координат единица масштаба.

 

Рис 1

Ось ох – ось абцисс.

Ось оу – ось ординат

О – точка пересечения осей, начало координат.

Положение всякой точки плоскости определяется ее расстоянием от осей координат. Эти расстояния называются координатами точки. Например, точка М имеет координаты х и у – М(х,у). Рис 1.

х – абцисса точки М, у – ордината точки М.

Координатам приписывают знаки, зависящие от расположения точки в различных частях координатной системы.

Пример. Построить точки: А(3,2); В(-1,4); С(-2,0); Д(-1,-1/2); Е(1,-1).

                                       Рис 2.

 

                                 0

 

 

Расстояние между двумя точками на плоскости М₁(х₁,у₁) и М₂(х₂,у₂) определяется по формуле М₁М₂ = (х₂-х₁)²+(у₂-у₁)².

Например, найти АВ, если А (1,2); В (-2,-2). Используя формулу, получим АВ=корень 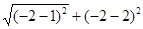= = = =5.

Соотношение, характеризующее зависимость между координатами х и у точек кривой называется уравнением этой кривой. Например: у+2х-1=0 – уравнение прямой, х²+у²=4 – уравнение окружности.

Координаты любой точки, лежащей на кривой, удовлетворяют уравнению кривой, а координаты точек, на кривой не лежащей, уравнению не удовлетворяют. Например, проверим лежит ли точка А (1,2) и В (0,1) на прямой у+2х-1=0. Для этого подставим координаты каждой точки в уравнение прямой.

1) А(1,2)-2+2-1 0, вывод: точка А не принадлежит прямой.

2)  В(0,1)-1-1=0, вывод: точка В лежит на прямой.

Любое уравнение первой степени относительно переменных х и у, называется линейным, оно есть уравнение прямой линии.

Ах+Ву+С=0, где А, В, С – вещественные числа, есть общее уравнение прямой.

Например, х+у-1=0, у=2х, х=3, у= -1. Эти уравнения – есть уравнения прямых.

Построим эти прямые на плоскости Рис 3. Положение любой прямой определяется двумя точками. Найдем точки пересечения прямой х+у-1=0 с осями координат.

Х	0	1
У	1	0

А(0,1); В(1,0). Через эти точки проводим прямую.

 

 

У=2х – прямая проходит через начало координат, т.к. координаты начала О(0,0) удовлетворяют уравнению прямой, подберем точку С(1,2) – лежащую на прямой, проведем прямую через точки О и С. Рис 4.

 

 

                  0

 

Прямая х=3 параллельна оси оу, прямая у=-1 параллельна оси ох. Рис 5.

 

					Рис.5

 

 

х

           0

 

 

 

Предыдущая1234567Следующая

Поделиться:

Воспользуйтесь поиском по сайту: