 |
Основные свойства неопределенного интеграла.
|
|
|
|
1. ( (f(x)dx)` = f(x). Производная от неопределенного интеграла равна подынтегральной функции.
(f(x)dx)` = f(x). Производная от неопределенного интеграла равна подынтегральной функции.
2. Дифференциал от неопределенного интеграла равен подинтегральному выражению. d( f(x)dx) = f(x)dx.
f(x)dx) = f(x)dx.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого.
 d(F(x)) = F(x) + C.
d(F(x)) = F(x) + C.
4. Постоянный множитель можно выносить за знак интеграла:
 , где к - число
, где к - число
5. Интеграл от суммы двух функций равен сумме интегралов от этих функций
 (f(x) +φ(x))dx =
(f(x) +φ(x))dx =  f(x)dx +
f(x)dx +  φ(x)dx.
φ(x)dx.
Для вычисления неопределенных интегралов от функций используют таблицу неопределенных интегралов, которая приводиться ниже.
Таблица неопределенных интегралов.
1.  хα dx = [xα+1 / (α +1)] +C, α ≠ -1, α Є R
хα dx = [xα+1 / (α +1)] +C, α ≠ -1, α Є R
2.  dx/x = ln│x│+C
dx/x = ln│x│+C
3.  ax = (ax/ln a)+C,
ax = (ax/ln a)+C,  exdx = ex+C
exdx = ex+C
4.  sinx dx = -cosx + C
sinx dx = -cosx + C
5.  cosx dx = sinx + C
cosx dx = sinx + C
6.  dx/(cosx)2 = tgx + C
dx/(cosx)2 = tgx + C
7.  dx/(sinx)2 = -ctgx + C
dx/(sinx)2 = -ctgx + C
8.  dx /
dx /  2-x2) = (arcsin x/a) + C
2-x2) = (arcsin x/a) + C
9.  dx /
dx /  2 – x2) = (-arccos x/a) +C
2 – x2) = (-arccos x/a) +C
10.  dx / a2 +x2 = 1/a arctg x/a +C
dx / a2 +x2 = 1/a arctg x/a +C
11.  dx / a2 +x2 = - 1/a arcctg x/a +C
dx / a2 +x2 = - 1/a arcctg x/a +C
12.  dx / a2 -x2 = 1/2a ln │x+a/x-a│ +C
dx / a2 -x2 = 1/2a ln │x+a/x-a│ +C
13.  dx /
dx /  a2 +x2) = ln │x+
a2 +x2) = ln │x+  2+x2)│ +C.
2+x2)│ +C.
Пример 1. Вычислить  (2х2 -3
(2х2 -3  -1)dx.
-1)dx.
Решение. Воспользуемся свойствами 4 и 5 неопределенных интегралов и первой табличной формулой.  (2х2 -3
(2х2 -3  -1)dx = 2
-1)dx = 2  х2 dx - 3
х2 dx - 3  х1/2 dx -
х1/2 dx -  dx=
dx=
= 2(x2/2) – 3[(х3/2 *2)/3] – x + C = x2 - 2  3 – x +C.
3 – x +C.
Пример 2.  (2/
(2/  -1/х + 4sinx)dx =
-1/х + 4sinx)dx =  2х –1/2dx – ln │х│ - 4cosx + C =
2х –1/2dx – ln │х│ - 4cosx + C =
= 2[(x1/2 *2)/1] – ln │x│ - 4 cosx +C = 4  -ln│x│- 4cosx + C.
-ln│x│- 4cosx + C.
Для вычисления неопределенных интегралов применяют следующие методы: метод непосредственного интегрирования, метод подстановки(метод замены переменной), метод интегрирования по частям.
Существуют элементарные функции первообразные которых элементарными функциями не являются. По этой причине соответствующие неопределенные интегралы называются «неберущимися» в элементарных функциях, а сами функции не интегрируемыми в элементарных функциях.
|
|
|
Например,  e –x^2 dx,
e –x^2 dx,  sinх2 dx,
sinх2 dx,  cosх2 dx,
cosх2 dx,  sinx/x dx,
sinx/x dx,  cosx/x dx,
cosx/x dx,  dx/lnx – «неберущиеся» интегралы, т.е. не существует такой элементарной функции, что F `(x) = e –x^2, F ` (x) = sinx2 и т.д.
dx/lnx – «неберущиеся» интегралы, т.е. не существует такой элементарной функции, что F `(x) = e –x^2, F ` (x) = sinx2 и т.д.
Тема 13. Определенный интеграл, его свойства.
Формула Ньютона - Лейбница.
Понятие интегральной суммы.
Пусть на отрезке [a, в] задана функция у = f(x). Разобьем отрезок на п элементарных отрезков точками деления а = х0, х1, х2, …, хп = в. На каждом элементарном отрезке [xi-1, xi] выберем произвольную точку Сi и положим
|
|
Эту сумму будем называть интегральной суммой для функции у=f(x) на отрезке [а, в]. Интегральная сумма зависит как от способа разбиения отрезка [a, в] на п частей так и от выбора точек С1, С2, …, Сп на каждом элементарном отрезке разбиения.
Геометрический смысл интегральной суммы.






 Пусть у = f(x) неотрицательна на отрезке [а, в]. Рис.1
Пусть у = f(x) неотрицательна на отрезке [а, в]. Рис.1

 y = f(x)
y = f(x)


 у
у

S1 S2 S3
0 а=х0 в1 х1 с2 х2 с3 х3 =в х
Рис.1
Пусть п=3, тогда а = х0, х1, х2, х3=в.
С1,С2,С3 точки, выбранные произвольно на каждом элементарном отрезке.
S1 = f1(C1) ∆x1 – площадь прямоугольника, построенного на первом отрезке разбиения, ∆х1 = х1-х0,
S2 = f2(C2) ∆x2 – площадь прямоугольника, построенного на втором отрезке разбиения. ∆х2 = х2-х1,
|
|
|
|
|
Это площадь ступенчатой фигуры, составленной из прямоугольников.
Понятие определенного интеграла.
|
|
|
|
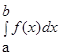 , т.е
, т.е  = lim Σ f(Сi)∆xi при
= lim Σ f(Сi)∆xi при
max ∆xi →0
Число а называется нижним пределом, b – верхним пределом, f(x) – подинтегральной функцией, f(x)dx – подинтегральным выражением.
|
|
|


