Некоторые свойства определенного интеграла.

1⁰. Значение определенного интеграла не зависит от обозначения переменной интегрирования, т.е.

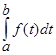 =  =  и т.д.

2⁰.  есть число.  

3⁰.  = - , а<b

4⁰. Постоянный множитель можно выносить за знак интеграла.

 = m , где m – const.

5⁰. Интеграл от суммы функций равен сумме интегралов.

6⁰. Если отрезок интегрирования разбит на части (a < c < b), то интеграл на всем отрезке равен сумме интегралов на каждой из частей.

x

b

c

a

 = ,

 

Существует еще ряд важных свойств определенного интеграла, которые подводят нас к формуле для вычисления определенного интеграла. Эта формула называется формулой Ньютона – Лейбница для f(x) непрерывной на [а; b].

 = F(b) – F(a), где F(x) некоторая первообразная для функции f(x).

Например,  - вычислить.

1)

1

Находим первообразную для функции х², т.е. неопределенный интеграл от х², произвольную постоянную С приравняем к нулю.

0

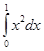   = x³/3 │ = 1/3 – 0/3 = 1/3

 

2) Подставим в первообразную х³/3 вначале значение верхнего предела, равного 1, затем значение нижнего предела, равного 0 вместо х.

π/2

2

π/6

Пример 1. Вычислить │= sin π/2 – sin π/6 = 1 – ½ = 1/2

-1

Пример 2. Вычислить │ = 2² – 2⁴/4 – [ (-1)² – ((-1)⁴/4)] =

= 4 – 4 –(1- (1/4)) = -3/4.

 Тема 14. Несобственные интегралы.

    Мы ввели понятие определенного интеграла от функции y = f(x) на отрезке [а; b], когда функция y = f(x) была интегрируема (и, следовательно, ограничена) на конечном отрезке [а; b]. Если отрезок интегрирования бесконечен, или функция не ограничена на отрезке интегрирования, то мы встречаемся с понятием несобственного интеграла.

    Несобственные интегралы с бесконечными пределами интегрирования.

    Рассмотрим интеграл с переменным верхним пределом . Такой интеграл есть некоторая функция от переменного верхнего предела, т.е.

    = Ф(х), х ≥ а.

    Определение.  – называется несобственным интегралом от функции f(x) на интервале [а;¥), вводится он как предел функции Ф(t) при t ®¥, т.е.

t→∞

    .

    Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, если предел бесконечен или не существует, то несобственный интеграл называется расходящимся.

∞

    Пример 1. Вычислить

x→∞

2

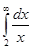
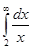     Решение  = lnx │ = lim lnx – ln2 = ∞ - ln2 = ∞. Интеграл расходится.

∞

    Пример 2. Вычислить

x→∞

∞

1

1

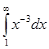 Решение  =  = x ^–2/-2 │ = -1/(2x ²) │= -1/2 (lim 1/x² – 1) = -1/2 (0-1) = 1/2

Интеграл сходится к ½.

 

    По аналогии определяется несобственный интеграл на интервале (-¥, b].

b→ −∞

 

    Определение сходимости  аналогично предыдущему.

    Вводится понятие несобственного интеграла на интервале (-¥; ¥).

, а – некоторое число.

    Интеграл  сходится, если оба интеграла  и  сходящиеся, если же один из них расходится, то  - расходится.

 

    Пример 3. Вычислить  .

0

    Решение. .

x→ -∞

-∞

    Рассмотрим  = e^x │ = e⁰ – lim e^x = e⁰ – 1/e^∞ = 1-0 = 1.

∞

     Интеграл сходящийся к 1.

x→ -∞

0

    Рассмотрим  = e^x │ =lim e^x - e ⁰ = e^∞ – 1 = ∞.

    Этот интеграл расходится, значит  - расходящийся несобственный интеграл.

    В курсе теории вероятностей встречается несобственный интеграл . этот интеграл называется интегралом Эйлера-Пуассона.

Доказано, что 2p).

    Несобственные интегралы от разрывных функций.

х→в-0

    Если y = f(x) непрерывна на [а; b), но lim f(x) = ¥, то вводится понятие несобственного интеграла от разрывной функции.

ε→0

ε→0

Определение. Если существует и конечен предел lim , где e > 0, то он называется несобственным интегралом от функции y = f(x) на интервале [а; b) и обозначается , т.е.  = lim

    В этом случае несобственный интеграл называется сходящимся, в противном случае – расходящимся.

    Аналогично вводится понятие несобственного интеграла

х→а+0

ε→0

= lim , если lim f(x) = ¥

δ→0

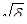    Пример 4. Вычислить  = 2х^1/2 │ = 2(  -lim ) =2.

Интеграл сходится к 2.

Тесты к теме 1.

1. На сколько периодов условно можно разделить развитие математики (по Колмогорову)?

1: 2

2: 4

3: 1

4: 5

2. К какому времени относится начало периода элементарной математики?

1-: XV в

2: I век н.э.

3: VI-V век до н.э.

4: XII в.

3. Что является предметом изучения науки “Математический анализ”?

1: функция

2: число

3: совокупность чисел

4: геометрические образы (точка, прямая, плоскость).

4. Перечислите основные черты математического мышления.

1: логические рассуждения, математическая интуиция;

2: доказательство;

3: математическая интуиция;

4: умение правильно считать.

5. Какие два вида умозаключений преобладают в математике?

1: моделирование, дедукция.

2: индукция, интуиция;

3: абстрагирование, интуиция;

4: индукция, дедукция;

6. Является ли математика искусством вычислять или наукой?

1: наука,

2: искусство вычислять.

Тесты к тема 2

1. Аксиома – составная часть дедуктивной системы. Это …?

1: Определение основных понятий данной науки.

2: Утверждение, требующее доказательства.

3: Утверждение, принимаемое без доказательств.

4: Некоторое логическое рассуждение.

2. Внутри дедуктивной системы не могут быть решены два вопроса. Какие из представленных?

1: Нужны ли доказательства аксиом? и Являются ли теоремы составной частью дедуктивного метода?

2: О смысле основных понятий. и Об истинности аксиом.

3:Можно ли определить в данной науке основные понятия? и Являюся ли доказательства составной частью дедуктивного метода?

3. Что представляет собой книга «Начала» Евклида?

1: Философское учение греческого философа и ученого Евклида.

2: Аксиоматическое построение геометрии.

3: Мифы Древней Греции.

4: Учение о параллельных прямых.

4 Кто из математиков почти одновременно с Н.И. Лобачевским подошел к созданию неевклидовой геометрии?

1: Гаусс, Бойяй

2: Лагранж, Ферма

3: Пуассон, Эйлер

4: Коши, Буняковский

5. В каком году был построен Императорский Казанский Университет?

1; 1804

2: 1800

3: 1850

4: 1900.

Тесты к теме 3.

1 Что представляет собой мнимая единица?

1: корень кв. из -1,

2: –1

3: (i)^2

4: (-1)^2

 

2. Найти корни квадратного уравнения х*х-х+1=0

1: Х1=1/2; Х2=3/2

2: Корней нет

3: Х1,2=1/2+-3/2i

4: Х1=2, Х2=-1

 

3. Произвести действия: Если Z1=1-2i, Z2= -2+3i, Найти Z1+Z2.

1: Z=1-i

2: Z= -1+i

3: Z=2+3i

4: Z=1+2i

 

4. Произвести действия: Если Z1=1-2i, Z2= -2+3i, Найти Z1*Z2.

1: Z= 4

2: Z=-8+3i

3: Z= -2+6i

4: Z=4-i

 

5. Найти Z”, если Z=2-i.

1: Z= -2-i

2: Z= -2+i

3: Z= 2+i

4: Z= 2

 

6. Представить число Z = -3 в виде комплексного числа. Указать его вещественную и мнимую части.

1: Z=3-3i,  Re Z=3, Im Z= -3

2: Z=-3+iо, Re Z=-3, Im Z=0

3: Z=3i,     Re Z=-0, Im Z=3

4: Z=3*i*i Re Z=0, Im Z=3

 

7. Найти корни квадратного уравнения х^2+4=0

1: Х=2

2: Корней нет

3: Х1,2=+-2i

4: Х= -2

 

 

8. Дано комплексное число Z= -3+2i. Найти координаты точки на плоскости хоу ему соответсвующие.

1; (-3;2)

2: (3,2)

3: (3, -2)

4: (-3,0)

 

9. Выделить вещественную и мнимую части числа Z=1-3i/5-i.

1: Z=1/5-3i

2: Z=4/13 – 7/13i

3: Z=1/26-3i

4: Z=1-i

Тесты к теме 4.

1. Даны точки М1(3,1); М2(2,3); М3(6,0); М4(-3,-1).

Определить какая из точек лежит на прямой 2х-3у-3=0

1: М1(3,1);

2: М2(2,3);

3: М3(6,0);

4: М4(-3,-1).

2. Дана прямая х-3у+2=0, точка М(1,у) лежит на этой прямой. Найти ордин ату этой точки.

1: у=-1,

2: у=0,

3: у=1,

4: у=5.

3. Дана прямая х-3у+2=0, точка Р(х,2) лежит на этой прямой. Найти абциссу этой точки.

1: х=0,

2: х=4,

3: х=1,

4: х= -4.

4. Даны точки А(-3,2) и В(1,6). Найти расстояние между ними АВ.

1: АВ=2.

2: АВ=4,

3: АВ=8,

4: АВ=4 * корень кв. из 2,

5. Даны четыре пары, указать какие из них являются параллельными прямыми.

1) 2х+3у-1=0 4х+6у+1=0

2) х+у+5=0 х-у-3=0

3) х+5=0 2х+5у=0

4) х-2у+3=0 2х-у-1=0

 

1: 2х+3у-1=0       4х+6у+1=0
2: х+у+5=0 х-у-3=0
3: х+5=0 2х+5у=0
4: х-2у+3=0 2х-у-1=0

6. Даны уравнения линий 1) у^2=х, 2)у=х^2+1, 3)х-у=0, 4)х^2 +у^2=1

Найти среди них уравнение прямой.

1: у^2=х,-

2: х - у=0,

3: у=х^2+1

4: х^2+у^2=1

7. Дано уравнение прямой у-2х+1=0. Записать это уравнение, как уравнение прямой с угловым коэффициентом. Найти отрезок в, отсекаемый прямой от оси ординат.

1: в= -1

2: в=1

3: в=1/2

4: в=0

8. Дана точка М(-1,2). Найти уравнение прямой проходящей через эту точку параллельно прямой 2х - у+3=0

1: х=2у

2: 2х - у=0;

3: х+у - 2=0;

4: 2х - у+4=0;

9. Среди заданных четырех прямых определить две перпендикулярные прямые.

1) х+у-5=0, 2)у=+х+2, 3)3х-3у+1=0, 4)2х=у

1: х+у-5=0, у=+х+2

2: х+у-5=0, 2х=у

3: у=х+2, у=2х

4: у=х+2, 3х-3у+1=0.

10. Дана прямая х+у-5=0. Найти точку А пересечения этой прямой с осью ох.

1: А(1,1);

2: А(-5,0);

3: А(5,0);

4: А(0,5)

Тесты к теме 5.

1. Написать уравнение окружности с центром в начале координат, радиусом равным 2.

1: х^2 + у^2 = 4

2: х^2 + у^2 = 2

3: (х – 2)^2 + (у – 2)^2 = 4

4: х^2 = 2

2. Х^2 + у^2 + 2х = 0. Дано уравнение окружности. Указать точку, лежащую на этой окружности: М1 (0, 0), М2 (1, 2), М3 (- 1, 3); М4 (0, 2).

1: М2(1, 2),

2: М1(0, 0),

3: М3(- 1, 3),

4: М4(0, 2),

3. Из четырех уравнений найти уравнение эллипса.

1) х/25 + у/16 = 1, 2) х^2/9 + у^2/4 = 1, 3) у^2 = 1 – х, 4) х^2 + у^2 = 9

1: нет уравнения эллипса

2: х/25 + у/16 = 1

3: х^2/9 + у^2/4 = 1

4: х^2 + у^2 = 9

4. Выделить уравнение гиперболы из четырех уравнений:

1) х/16 - у/9 = 1, 2) х^2 – у^2 = 1, 3) х^2  + у^2 = 1, 4) х^2 + 2у^2 = 1

1: х^2 + 2у^2 = 1

2: х/16 - у/9 = 1,

3: х^2  + у^2 = 1,

4: х^2 – у^2 = 1,

5. Написать уравнение эллипса, зная, что малая полуось в=3, расстояние между фокусами F1 F2= 8.

1: x^2/64+y^2/9=1

2: x^2/16+y^2/9=1

3: x^2/8+y^2/9=1

4: x^2/25+y^2/9=1

6. Написать уравнение эллипса, если большая полуось а=в, эксцентриситет Е=0,5.

1: x^2/6+y^2/2=1

2: x^2/6+y^2/9=1

3: x^2/36+y^2/27=1

4: x^2+y^2=1

7. х^2/18 – y^2/4,5=1 Дано уравнение гиперболы. Написать уравнение асимптот.

1: y=+-х

2: у=+-1/2х;

3: y=+-1/18 х

4: y=1/3х

8. На параболе у^2=6х найти точку с абциссой равной 6

1: М(0,6)

2: М(6,6)

3: М(6,0)

4: М1(6,6) и М2(6,-6)

9. Дана парабола у^2=6х. Найти координаты фокуса F.

1: F(3/2;0)

2: F(3,0)

3: F(0,6)

4: F (0,3)

10. Написать уравнение гиперболы, если а=9, в=4.

1: x/81 - y/4=1

2: x^2/9+y^2/4=1

3: x^2/81 - y^2/16=1

4: x^2 - y^2=9

Тесты к теме 6.

1. Вычислить определитель!2 3!

                                            !4 5!

1: -2,

2: 22,

3: 2,

4: 7,

2. Вычислить определитель!2 3!

                                            !4 5!

1:-5,

2: 10,

3: 1,

4: 0,

3. Справедливо ли равенство!2 8 10!  !1 4 5!

                                            !1 3 -1! =2!1 3 –1!?

                                            !2 0!1    !2 0 1!

1: Нет,

2: Да,

4. Дан определитель!1 5 3! Найти минор М21 к элементу а21 = 6.

                               !6 1 0!

                               !3 0 –1!.

1: М21= 0,

2: М21= -2,

3: М21= 1,

4: М21= 4,

5. Дан определитель!1 5 3! Найти алгеброическое дополнение А21 к

                               !6 1 0!               элементу а21 = 6.

                               !3 0 –1!.

1: А21= 2,

2: А21= -2,

3: А21= 1,

4: А21= 4,

6. Если элементы второй строки определителя умножить на соответствующие алгебраические дополнения и произведения сложить, то получим:

1: отрицательное число,

2: ноль,

3: любое число,

4: величину определителя,

7. Дана система уравнений х+у=3

                                          2х-3у=1.

Имеет ли эта система единственное решение?

1: Да,

2: Нет.

8. Дана система уравнений х - у=1

                                          4х-4у=4

1: система не имеет решения,

2: система имеет единственное решение,

3: система неопределенная,

9. Дана система 2х-3у+5z=1

                        х+у-z =2

                        3х-у-2z=3

Указать свободные члены:

1:(5, -1, -2);

2: (2, 1, 3);

3: (-3, 1, -1);

4: (1, 2, 3);

10. Может ли определитель иметь три строки и два столбца?

1: Да.

2: Нет,

Тесты к теме 7.

1. Выберите правильное утверждение:

1) Матрица может иметь любое число строк и столбцов.

2) Матрица всегда имеет одинаковое число строк и столбцов.

3) Матрица не может состоять из одной строки.

4) Матрица не может состоять из одного столбца.

Ответ: 1)

Ответ: 2)

Ответ: 3)

Ответ: 4)

2. Может ли матрица состоять из одного элемента?

1: Да,

2: Нет,

3: Да, если это элемент не равен нулю.

3. Умножить матрицу А=(1, -1, 3, ½) на число (-2):

1: -7

2: (1, -1, 3, -1)

3: (-2, -1, 3, ½)

4: (-2, 2, -6, -1)

4. Можно ли сложить матрицы 2*2 и 3*3?

1: Нет

2: Да.

5. Можно ли перемножить матрицы соразмерности 2*3 и 3*4?

1: Нет.

2: Да.

6. Транспонирование матриц – это:

1) Перестановка местами двух столбцов.

2) изменение знака у всех элементов,

3) Перестановка местами двух строк,

4) перестановка местами строк и столбцов,

Ответ: 1)

Ответ: 2)

Ответ: 3)

Ответ: 4)

7. Если размерность исходной матрицы равна 6*7, то транспонированная матрица будет иметь размерность:

1: 6*6

2: 6*7

3: 7*6

4: 7*7

8. Единичная матрица – это:

1: Матрица, у которой все элементы равны 1.

2: Матрица, у которой элементы главной диагонали равны 1, а остальные нули

3: Матрица, определитель которой равен 1.

4: Матрица, содержащая только один элемент.

9. Если А=(1,3, -2), В= (-1)

                                   (0)

                                   (2), то А*В равно

1: -5

2: (-1 0 –4)

3: (-1)(0)(-4)

4: Перемножить нельзя

Тесты к теме 8.

1. N – множество натуральных чисел. Какое из множеств является его подмножеством: А= {2, 4, 6, 8…}, В= (N2, N3, N4,…}; С= {1, 1/2, 1/3, 1/4, …};

Д= {1, 0, 1}?

1: В,

2: А,

3: С,

4: Д,

2. Найти пересечение множеств А= {1, 3, 5, 7, 9} и В= {2, 4, 6, 8}.

Ответ: пустое множество,

1: {1}

2: {1,2,3,4,5,6,7,8}

3: {0}

3. Найти объединение множеств А и В, если А = {1,3,5,7,9}; B = {2,4,6,8}.

1: AUB = {0}

2: AUB = 0    

3: АUB = {1, 2, 3, 4, 5, 6, 7, 8, 9}

4: AUB = {2,4,6,8}

4. Найти разность множеств А \ В, если А = {1,2,3,4}; B = {0,1,2}.

1: А\B = {3, 4}

2: A\B = {0,3,4}

3: A\B = {0,1,2}

4: A\B = {1,2,3}

5. Если /х/<2, то в виде двух неравенств его можно записать так:

1: -2<x<2

2: -2<=x<=2

3: 0<x<2

4: -2<x<0.

6. Если /х-1/<E, то E – окрестность точки 1 можно записать так:

1: -Е<x<Е

2: 1-Е<x<1+Е

3: 0<x<1+Е

4: -Е<x<0.

7. Если х принадлежит [-1, 3]. Какое из значений может принять х?

1: x<-1

2: -x= -3

3: x=0

4: x=4.

8. Если х не принадлежит (-2, 2). Какое из значений может принять х?

1: x= -1.

2: -x= 0

3: x=2

4: x= -4

9. Если –2<х<=0, то решением является:

1: (-2, 0)

2: (-2, 0]

3: (-2, 2)

4: [-2, 0].

10. Найти пересечение множеств (-2, 2) и (-3, 1):

1: (-3, 2)

2: [0, 1]

3: (-2, 1)

4: [-2, 0].

Тесты к теме 9. «Функция. Классификация функций».

1. Найти область определения функции у = (х-2) / (х^2 – 9)

1: (0, 2)

2: (-00, -9) U (9, 00).-

3: (2, 3).

4: (-00, -3) U (-3,3) U (3,00).

2 Найти область определения функции у = (х-1)^1/2

1: (-00, 00).

2: (0, 00).

3: [1, 00).

4: x = 0

3. Найти область определения функции у = lg(2+х)

1: (-2, 00).

2: [2, 00).

3: (-00, 00).

4: x = 0

4. Найти значения функции у = х^2/ (х-1) в точке х = 0.

1: у = -1.

2: у = 0.

3: у = 00.

4: у = 2

5. Найти значения функции у = х^2/(х-1) в точке х = 1.

1: у = -1.

2: у = 1.

3: не существует.

4: у = 2

6. Найти значения функции у = х^2/(х-1) в точке х = (а^2) +1.

1: у = не существует.

2: у = ([а^2]+1)/а^2.

3: у = -1.

4: у = [(а^2 + 1)^2]/а^2.

7. Дана функция у = (sinх)^2 +5. К какому классу функций она принадлежит?

1: Трансцендентная.

2: алгебраическая.

8. Написать целую алгебраическую функцию второй степени, в общем виде.

1: у = х^2.

2: у = [(А0)*х^2] + (А1)*х + А2.

3: у = [(А0)х^2]+1.

4: у = (х^2)/(х+1)

9. Указать дробно-рациональную функцию из заданных функций:

1) у=2*х/(1+х+х^2); 2) у=х/(sinх); 3) у=(2)^х/2; 4) у= lg(х+2)/(х-2)

Ответ: 1).

Ответ: 2).

Ответ: 3).

Ответ: 4).

10. Дана сложная функция у = [sin (1-х)]^2. Представить ее в виде цепочки простых функций.

1: U = sin x, V = U-1, y = (U-1)^2.

2: U = sin(1-x), y = U^2.

3: U = 1-х, V = sinU, y = V^2.

4 y = [sin(1-x)]^2 – простая функция

 

Тесты к теме 10.

х→ 00

1. Найти: lim  [2/(x-1)];

1: 2

2: 0

3: не существует.

4: 1

х→ 1

2. Найти: lim  [2/(x+2)];

1: не существует.

2: 0

3: 2/3

4: 1/2

х→ -3

3. Найти: lim  [(х²+5х+6)/(x²-9)];

1: 0

2: 5/6

3: 1/2

4: 1/6

х→ 00

4. Найти: lim  [(1+х²) / (x³+2х²+х-1)];

1: 1

2: 0

3: -1

4: 00

х→ 0

5. Найти: lim  [х / sin x];

1: 1

2: 0

3: не существует.

4: 00

х→ 0

6. Найти: lim  [sin5x / x];

1: не существует.

2: 0

3: 00

4: 5

х→ 00

7. Найти: lim  [1+(1/(x+2))]^х;

1: 00

2: 1

3: е

4: не существует

х→ 00

8. Найти: lim  [1+(1/x)]^2х;

1: е²

2: е

3: 1

4: 00

9. Является ли функция у=х² непрерывной в точке х=2

1: Нет

2: Да

10. Является ли функция у=1/(2х+1) непрерывной в точке х=1

1: Да

2: Нет

Тесты к теме 11.

1. Найти приращение функции у=1/х, если х=1, ∆х=0,1.

1: - 1/11,

2: 0,1,

3: 0,01,

4: - 1,

2. Пользуясь определением производной, найти производную от функции у=х^3.

1: 3х^2∆х,

2: х^2,

3: 3х^2 - 1,

4: 3х^2,

3. Найти производную от функции у=хe^x, в точке х=0.

1: e+e^-1,

2: e^1,

3: 1,

4: 0,

4. Найти производную от функции у=х^5 – ¼x^4 + 3, в точке х.

1: 5x^4 – x^3 + 3,

2: 5х^4 – x^3,

3: 5x^4 – x^4 + 1,

4: 3,

5. Найти производную от функции у=sinx/cosx

1: sinx - cosx,

2:-cosx/sinx,

3: 1/cosx^2,

4: 1,

6. Найти дифференциал функции у=х^3 – 1.

1: 3(dx)^2,

2: 3x^2,

3: 3dx,

4: 3х^2dx,

7. Дана функция у=3х^2 – х + 1. Найти у``

1: 6x,

2: 6,

3: 1,

4: 6x^2,

8. Найти у```, если у=х^6 – 1/4х^4+1/2x^2+2.

1: 120х^3 – 2x,

2: 120x^3,

3: 120x^3 – 2x +2,

4: 120,

9. Найти у```, если у=(х^2)*e^x.

1: 2e^х + 4xe^x +(x^2)*e^x,

2: 2xe^x+(x^2)*e^x,

3: 2xe^x + e^x,

4: 2e^x,

Тесты к теме 12.

1. Найти первообразную для функции у = х.

1: х – 2

2: 2х,

3: 2х^2,

4: (х^2)/2.

2. Даны функции F1 (x) = sinx – 8, F2 = sinx +3. Первообразными для какой функции они являются?

1: х,

2: cosx,

3: -cosx,

4: -х.

3. Найти производную от функции $ln(x^2 +1)dx.

1: 2х/ [(x^2) +1],

2: ln[(х^2)+1].

3: ln((х^2)+1)dx,

4: 1/((x^2)+1)

4.  Найти дифференциал от функции $x arcsin2x dx.

1: x arcsin2x dx.

2: arcsin2х,

3: arcsin2x dx,

4: [arcsin2x +2x/ (1-4(x^2))^1/2]dx.

5. Вычислить $d(2^x^2)

1: (2^х^2) (ln2)2x,

2: (2^х^2)+C.

3: (2^х^2)dx,

6. Вычислить интеграл $(x^2 -3)dx.

1: [(x^3)/3x] – 3x,

2: [(х^3)/3] – 3х +С.

3: (3х^3)+C,

4: [(x^2)-3]+C

7. Справедлива ли формула $U(x) V(x)dx = $U(x)dx*$V(x)dx?

1: Нет

2: Да.

8. Можно ли вынести постоянный множитель за знак интеграла?

1: Да.

2: Нет

9. Указать какие из интегралов является «неберущимися» $sin(x^2) dx, $lnx/x dx, $[1+ (x^1/3)] dx.

1: sin(x^2) dx.

2: $ lnx/x dх,

3: $[1+x^1/3]dx.

10. Указать какие из интегралов является «неберущимися» $(e)^-x^2 dx,

$xe^x^2, $x^2 e^-x^2 dx, $xe^-x^2 dx.

1.$xe^-x^2 dx,

2: $ xe^x^2 dх,

3: $e^-x^2 dx

4: $[(x^2) (e^-x^2)] dx.

Тесты к теме 1 3.

1. Вычислить интеграл в пределах (1, 00) от функции dx/(x^2).

1: 1,

2: расходится,

3: 0,

4: -1,

2. Вычислить интеграл в пределах (0, 00) от функции e^-x dx.

1: расходится,

2: 1,

3: 0,

4: -1,

3. Вычислить интеграл в пределах (-00, 00) от функции e^-2x dx.

1: -1,

2: 0,

3: 1,

4: расходится,

4. Вычислить интеграл в пределах (0, 1) от функции dx/x.

1: 2,

2: сходится

3: расходится,

4: 0,

Тесты к теме 14.

1. Зависит ли интегральная сумма для функции у=f(x) на отрезке [а, в] от способа разбиения отрезка на 10 частей?

1: Да,

2: Нет,

2. Зависит ли интегральная сумма для функции у=f(х) на отрезке [а, в]от выбора точек Сi на i элементарном отрезке, i = 1,2,…,п?.

1: Нет,

2: Да,

3. Можно ли записать интеграл в пределах (0, 2) от функции (sinx^2 – 3x^1/2)dx = $ в пределах от (0, 2) от функции sinx^2 dx + 3$ в пределах (0, 2) от функции х^1/2 dx?

1: Да,

2: Нет,

4. Можно ли записать интеграл в пределах (0, 2) от функции f(x)dx = интегралу в пределах (0, 1) от функции f(x)dx + интеграл в пределах (1, 2) от функции f(x)dx.

1: Нет,

2: Да,

5. Вычислить интеграл в пределах (4, 3) от функции (x^1/2)dx.

1: 2/3,

2: 19,

3: 38/3,

4: 1,

6. Вычислить интеграл в пределах (0,П/2) от функции (sinx)dx.

1: 1/2,

2: -1,

3: 0,

4: 1,

7. Вычислить интеграл в пределах (1, 3) от функции dx/х^2.

1: -1/3,

2: 2/3,

3: 1,

4: 0,

8. Найти значение интегральной суммы для f(x) = 1 на отрезке [a, в].

1: в-а,

2: ав,

3: 1/в-а,

4: 2,

9. Верно ли равенство интеграл в пределах (0, 2) от f(x)dx.= - интеграл в пределах (2, 0) от f(x)dx?

1: Нет.

2: Да,

 

 

.

 

 

Предыдущая1234567Следующая

Поделиться:

Воспользуйтесь поиском по сайту: