 |
3.3.7. Уравнение Бренстеда. 3.3.7. Величина и смысл коэффициентов Бренстеда
|
|
|
|
3. 3. 7. Уравнение Бренстеда
В 1920-х годах Бренстед и Педерсен получили экспериментальные данные, показывающие, что чем сильнее соединение AiH (или Bi) как кислота (или основание), тем оно эффективнее как общий кислотный (основной) катализатор. Это означает, что поведение кислот и оснований при ионизации (обмен протона с растворителем) тесно связано с их поведением как общих кислотных и основных катализаторов. Соотношение межу силой кислоты или основания и скоростью катализируемых ими реакций называется каталитическим законом Бренстеда. Этот закон записывается следующим образом:
lgka=lgKa(AH)+const,
lgkb=-lgKa(BH+)+const,
где ka и kb -константы скорости реакций, катализируемых кислотами и основаниями соответственно; Ka(AH) и Ka(BH+) - константы диссоциации катализаторов; и - коэффициенты Бренстеда, не зависящие от природы АН или BH+, а зависящие только от типа реакции и условий ее проведения. Поскольку lgKa=-рКа,
lgka=-рKa(AH)+const, (3. 23)
lgkb=рKa(BH+)+const. (3. 24)
Другими словами, изменение свободной энергии Go при кислотно-основном равновесии пропорционально изменению свободной энергии активации G# (раздел 3. 3. 7. г) при переходе от реагентов к переходному состоянию переноса протона.
Для кислот
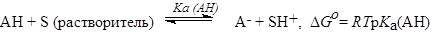

-G# пропорционально Go.
Для оснований:


G# пропорционально Go
Уравнение Бренстеда является одним из соотношений линейности свободных энергий (так как G# пропорционально Go и тесно связано с уравнением Гаммета (разд. 3. 4. 5).
3. 3. 7. Величина и смысл коэффициентов Бренстеда
Общий кислотный и общий основной катализ с медленным переносом протона
|
|
|
В типичном случае общего кислотного или общего основного катализа перенос протона от АН к R или от RH к В является самой медленной стадией общего многостадийного процесса (разд. 3. 3. 6. в). Рассмотрим, например, энергетический профиль реакции для общего основного катализа, когда скорость реакции контролируется переносом протона от реагента RH к катализатору Во (рис. 3. 11, а). Энергетический профиль можно представить как результат наложения друг на друга отдельных параболических кривых потенциальной энергии для RH и ВоН+, соответствующих растяжению связи R-H при переходе от (RH+Bo) к переходному состоянию (R... H... Bo) и растяжению связи Во-Н при переходе от (BoH++R-) к этому же переходному состоянию (последний процесс происходит в обратной реакции; (рис. 3. 11. б).

Рис. 3. 11. Реакция переноса протона (а), ее моделирование двумя кривыми растяжения связей (б) и вывод соотношения Бренстеда (в)
Теперь изменим катализатор Во на немного более слабое основание Bi. Энергия сопряженной кислоты BiH+ будет немного выше энергии ВоН+, а если Bi и Во не очень отличаются по типу и строению (например, Bi и Во - два замещенных в кольцо анилина; однако нельзя брать случаи, когда, например, Вi=анилин, а Во=СН3О-), то форма двух кривых BH+ будет одинакова, и просто одна парабола будет вертикально сдвинута относительно другой без изменения (рис. 3. 11, в). Разность свободных энергий активации G# для двух реакций RH+Во и RH+Bi в таким случае будет приблизительно пропорционально разности свободных энергий Gо для равновесной диссоциации ВоН+ и BiH+. Если представить ветви парабол в области пересечения параллельными прямыми, то из рис. 3. 11, в следует:
G#=  Gо,
Gо,
т. е.
lg[kb(i)/kb(0)]=  lg[Kb(i)/Kb(0)]=-[pKa(BH+)-pKa(BoH+)].
lg[Kb(i)/Kb(0)]=-[pKa(BH+)-pKa(BoH+)].
Таким образом, величина коэффициента Бренстеда (и, аналогично, для кислотного катализа величина ) зависит от наклона кривых для RH и BH+ в точке их пересечения. Как показано на рис. 3. 12, величина коэффициента Бренстеда должна лежать в пределах от 0 до 1, т. е.
|
|
|
01 для реакции RH+B R-+BH+
и
01 для реакции R+АН RН++А-.
Если кривые пересекаются в вершине параболы RH, то =0 (рис. 3. 12, а), и перенос протона происходит без затраты энергии. Такую реакцию практически реализовать очень трудно, так как при больших скоростях переноса протона лимитирующей стадией может стать процесс образования комплекса соударения RH с В, и наблюдаемая величина практически будет следствием диффузионного контроля, а не характера пересечения энергетических кривых. Следовательно, 0, 0, если скорость переноса протона контролируется диффузией реагентов. Если кривые пересекаются в вершине парабола ВН+, то =1 (рис. 3. 12, в). В этом случае реагенты переходят в продукт путем постепенного подъема по склону энергетической поверхности, и " яма" на кривой ВН+ фактически является высшей точкой поверхности. Очевидно, что 1 (1) характерны для очень медленных процессов переноса протона (реакция очень слабых кислот с очень слабыми основаниями).
Наиболее часто в практике встречаются случаи, когда 0< ()< 1 (рис. 3. 12, б).

Рис. 3. 12. Физический смысл коэффициента Бренстеда. а - tg0; по энергии и структуре переходное состояние (R... H... B) очень близко к реагентам (RH+B). б - обычная реакция. в - переходное состояние очень близко к продуктам реакции (R-+BH+); tg1
Таким образом, величина коэффициента Бренстеда проливает свет на структуру переходного состояния. Если () малы по величине, то структура переходного состояния близка к структуре реагентов, активационного барьера почти нет, и лимитирующей стадией может быть диффузия реагентов друг к другу. Если () приближается к единице, то структура переходного состояния близка к структуре продуктов реакции.
Общий кислотный и общий основной катализ с быстрым переносом протона
Если перенос протона между катализатором и субстратом происходит быстро и при этом вначале устанавливается кислотно-основное равновесие с образованием сопряженной кислоты (или сопряженного основания) субстрата, которая дальше превращается в продукты (енолизация ацетальдегида; разд. 3. 3. 6. в), то смысл коэффициента Бренстеда будет немного иной. Для общего кислотного катализа
|
|
|


На основании уравнения (3. 22) можно написать
Кнабл=Ка(АН). К1. к2
или
lgкнабл=lgКа+lgК1+lgк2
Применяя уравнение Бренстеда (3. 24) для основного катализа на второй стадии, получим
lgкнабл= -lgКа(АН)+const.
Следовательно,
lgкнабл=(1-)lgКа(АН)+lgК1+const.
К1 не зависит от природы катализатора АН, и поэтому полученное соотношение будет нормальным уравнением Бренстеда для кислотного катализа с коэффициентом
=1- (3. 25)
Это тоже очень важное соотношение. Когда серия кислот АН реагирует с одним и тем же основанием В, сумма коэффициентов для прямой реакции

и обратной реакции

равна единице, поскольку
lgК=lgкАН-lgka= -pKa(АН)+pKa(BH+),
где К=кАН/кА- - константа равновесия АН+В ВН++А-.
Подставляя уравнение (3. 23), получаем
lgкА-=(1-)рКа(АН)+lgКа(ВН+)+const.
Таким образом, коэффициент для обратной реакции равен 1-, где - коэффициент для прямой реакции кАН.
|
|
|


