Каковы геометрич. допущения инженерных методов определения напряжений (внутр. усилий) в соор-ях и из элементах.

Для решения задачи оценки прочности достаточно знать либо напряжения в связях, либо их деформации. Однако как видно из выражений (3.8), (3.10), (3.12), ни одна из этих групп уравнений (уравнения статики, геометрические и физические зависимости) отдельно не решается. Решение в окончательном виде на основе имеющихся математических методов получено только для ограниченного круга задач. Эти задачи рассматриваются в теории упругости. В практике проектирования большинства строительных конструкций обычно используют более простые инженерные методы определения напряжений. Из множества сооружений мы будем рассматривать только те, к которым эти методы применимы.

Инженерные методы оценки напряженно деформированного состояния основаны на геометрических допущениях (гипотезах). Вводимые гипотезы позволяют получить описание состояния бесконечного количества внутренних связей через конечное число параметров. Эти гипотезы зависят от соотношения размеров элементов сооружения.

Если какой-либо размер элемента мал по сравнению с двумя другими, как, например, в плитах, оболочках, складках, мембранах, то с большой достоверностью можно считать, что в направлении малого размера связи деформируются по линейному закону. Поэтому для тонкостенных конструкций в направлении малого размера принимается гипотеза Кирхгофа - Лява о прямой недеформированной нормали: нормаль перпендикулярная к срединной поверхности остается перпендикулярной к ней в деформированном состоянии и не изменяет своей длины.

Если элементы имеют два малых размера по сравнению с третьим - это нити, стержни, то используется допущение Сен-Венана в направлении двух малых размеров. Оно заключается в том, что сечения плоские и перпендикулярные к оси до деформации стержня остаются плоскими и перпендикулярными к оси после его деформации и не изменяют своей формы.

Когда размеры элементов сооружения во всех направлениях одинакового порядка (такие элементы называются массивами), геометрические гипотезы ввести затруднительно. Поэтому для таких сооружений инженерный метод не применим.

Приняв геометрические допущения, мы получаем возможность в теории тонкостенных конструкций положение всех связей определять через характеристики срединной поверхности, а в теории стержней - через характеристики оси. Гипотеза прямой недеформированной нормали позволяет деформированное ее положение определить пятью параметрами: тремя линейными (x₁, x₂, x₃) и двумя угловыми (x₄, x₅) (рис. 4.1). Таким образом, чтобы установить положение всех связей, достаточно знать всего пять параметров, что аналогично замене бесконечного количества микросвязей между материальными точками пятью макросвязями.

Гипотеза плоских недеформируемых сечений дает возможность определить положение сечения в деформированном состоянии стержня шестью параметрами: тремя координатами (x₁, x₂, x₃) и тремя углами поворота (x₄, x₅, x₆) (рис. 4.2), то есть, бесконечное количество микросвязей заменить шестью макросвязями. Если деформация стержня происходит в одной плоскости, то остается всего три параметра (три макросвязи), указывающих положение всех связей в сечении (две линейных и одна угловая).

При построении методов расчета вводится еще одно допущение геометрического характера - о малости перемещений, которое дает возможность в уравнениях статики использовать геометрические параметры (расстояния, углы), взятые в недеформированном состоянии.

 

Внутренние усилия в каком либо сечении стержня. Виды внутр. усилий

Рассмотрим различные виды деформации прямолинейного стержня. Теория плоских сечений постулирует отсутствие давления продольных волокон друг на друга, т. е. отсутствие нормальных связей между волокнами (существуют только касательные связи), поэтому будем рассматривать стержень как множество несвязных волокон, параллельных оси.

При рассмотрении любой деформации декартовые координатные оси будем располагать так, чтобы ось z совпадала с осью стержня, а оси x и y располагались в плоскости сечения стержня перпендикулярного его оси по направлениям осей симметрии сечения, если они имеются.

 

Осевое растяжение

Рассмотрим стержень прямоугольного сечения, верхняя грань которого закреплена, а к нижней грани точно по центру сечения подвешен груз (рис.4.3). Действие груза приведет к тому, что внутренние связи начнут растягиваться (удлиняться) вдоль оси стержня z. Так как сечение плоское до деформации должно оставаться плоским, и после деформации и не должно менять свою форму, расстояние между двумя соседними сечениями l увеличится на величину Dl (рис.4.3), настолько же удлинятся и связи. Во всех других направлениях деформации отсутствуют, то есть.

e_z = Dl/ l, e_x = e_y = 0, g_xy = g_xz = g_zy = 0 .

Разделим стержень сечением  на две части и рассмотрим одну из них,

 

например, верхнюю. Придерживаясь правил принятой нами концепции сил, разорванные при этом связи необходимо заменить возникающими в них усилиями - напряжениями. По соотношению (3.10) эти напряжения будут равны

s_z = E×e_z, s_x = s_y = t_xy = t_xz = t_zy= 0 .

(рис.4.3). Так как деформации одинаковы, то и напряжения по сечению будут распределены равномерно, то есть s_z = const. Следовательно, равнодействующая N напряжений s_z должна быть приложена в центре тяжести сечения и направлена вдоль оси стержня. Эта равнодействующая называется продольной силой и значение ее равно

(4.1)

(здесь А - площадь поперечного сечения стержня).

Знак продольной силы определяется знаком s_z (продольная сила положительна, если она растягивает стержень, и отрицательна, если его сжимает).

 

Чистый изгиб

Чистый изгиб будет иметь место, если к горизонтально расположенному стержню подвесить на одинаковом расстоянии от опор два одинаковых груза, как показано на рисунке 4.4. a)

При такой деформации продольные волокна стержня будут искривляться по дуге окружности, поперечные сечения, плоские до деформации, останутся плоскими и перпендикулярными оси после деформации, но повернутся на некоторый угол j. Длина осевых (нейтральных) волокон не изменится, нижние волокна удлинятся, а верхние укоротятся (рис.4.4). Как и при осевом растяжении, будут только продольные деформации связей. Если, учитывая гипотезу о малости перемещений, закон изменения деформаций по высоте сечения считать линейным, то относительное удлинение каждой связи будет зависеть от расстояния между нейтральным волокном и этой связью y и от изменения кривизны стержня в рассматриваемом сечении k = j / l .

Таким образом,

e_z = Dl/ l =k×y, e_x = e_y = 0, g_xy = g_xz = g_zy = 0 .

в)

 

 

Если разделить стержень любым произвольным сечением на две части и заменить разорванные связи усилиями в них (напряжениями) (рис.4.4, г), то на основании соотношения (3.10)

s_z=E×e_z= E×k×y, s_x = s_y = t_xy = t_xz = t_zy. (4.2)

Нормальные напряжения s приводятся к паре сил с моментом

(4.3)

который называется изгибаим моменто относительно оси x.

Подставля оотношения (4.2) в (4.3), получим

.

представляет собой геометрическую характеристику сечения стержня и называется моментом инерции сечения относительно оси x. С учетом этого обозначения будем иметь

M_x = E×k×I_x. (4.4)

Знак момента определяется знаком координаты y и напряжения s_z и совпадает со знаком кривизны. Из соотношения (4.2): k = s_z / (E×y). Подставляя это выражение в (4.4), получим формулу, связывающую изгибающий момент с напряжениями в связях

M_x = s_z×I / y. (4.5)

Геометрические характеристики часто встречающихся сечений приведены в таблице 4.1, а прокатных профилей - в таблицах

Сдвиг (срез)

Деформацию сдвига (среза) можно наблюдать на оси грузового устройства (рис.4.5). Приложенная к крюку нагрузка будет стремиться опустить его вниз, перерезая при этом ось, поддерживающую крюк, по сечению AC, совпадающему с боковой гранью крюка. Сдвигу (срезу) волокон стержня по этому сечению будут препятствовать внутренние связи, но при этом в них появятся деформации D, которые принято определять через угол сдвига (рис. 4.5). В соответствии с гипотезой плоских сечений деформация сдвига для всех связей в сечении AC одинакова, а вследствие малости перемещений

g = tg g = D / l.

 

Все остальные деформации связей в сечении отсутствуют, то есть

 

e_z = e_x = e_y = 0, g_zx = g_yx = 0 .

Если в плоскости среза разрезанные связи заменить напряжениями (рис.4.5), то в соответствии с физическими соотношениями (3.10)

 

s_z = s_x = s_y = 0, t_zy = G×g, t_zx = t_xy = 0. (4.6)

Равнодействующая касательных напряжений в данном случае называется поперечной силой при сдвиге. С учетом равномерного распределения t_zy по сечению ее значение будет равно

. (4.7)

Знак поперечной силы определяется знаком касательных напряжений

 

Поперечный изгиб

В отличие от чистого изгиба при поперечном изгибе стержня (рис.4.7) происходит не только удлинение и укорочение составляющих его волокон, но и сдвиг этих волокон относительно друг друга. Поэтому сечение разворачивается по отношению к продольной оси и искривляется (депланирует), перестает быть плоским. Гипотеза плоских сечений позволила во всех рассмотренных выше случаях получить зависимости между деформациями и напряжениями на основе простых геометрических соображений, в данном случае она оказывается неприемлемой. Дмитрий Иванович Журавский (1821-1891) предложил оригинальный выход из этого положения. Он ввел предположение, что депланация сечений при поперечном изгибе не оказывает влияния на нормальные напряжения в поперечных сечениях стержня, то есть, как и при чистом изгибе

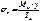, (4.11)

а сказывается только на величине и распределении по сечению касательных напряжений t. По Д.И. Журавскому

, (4.12)

где b - ширина сечения в уровне действия напряжения , S - статический момент площади выше (ниже) этого уровня относительно центра тяжести сечения.

Равнодействующие напряжений в сечении - продольная сила N, моменты (изгибающие M_x, M_y и крутящий момент M_z) и поперечная сила (Q_x или Q_y) называются внутренними усилиями и представляют собой интегральные (суммарные) характеристики напряжений.

Для всех остальных видов деформации внутренние усилия можно получить на основе выведенных формул (4.1) - (4.12). Так как при малых перемещениях справедлив принцип суперпозиции, то все сложные деформации и соответствующие им усилия рассматриваются как сумма независимых простых деформаций или усилий. Рассматриваемые ниже виды напряженного состояния можно рассматривать как примеры использования этого принципа.

 

27. Статический способ определения внутр. усилий и на чем он основан

Пусть под действием приложенной внешней нагрузки (рис.4.10) стержень находится в равновесии (дана самоуравновешенная система сил), т. е. для внешних сил выполняются условия

, , (4.14)

,

 

Любая часть стержня должна находиться в равновесии под действием внешней нагрузки и внутренних усилий. Разделим стержень сечением abсd на две части. Чтобы не нарушить их равновесия, усилия в рассеченных связях заменим интегральными силовыми характе-ристиками (рис. 4.10). Ими должны быть: продольное усилие N, изгибающие моменты M_x, M_y; крутящий момент M_z; поперечные силы Q_x,Q_y (шесть параметров соответствуют шести степеням свободы плоского сечения или шести макросвязям). Для части стержня также должны быть справедливы уравнения равновесия (4.14), но только теперь в них войдут неизвестные внутренние усилия

S x = P_x + Q_x = 0, S m_x = M_px + M_x = 0,

S y = P_y + Q_y = 0, S m_y = M_py + M_y = 0, (4.15)

S z = P_z + N = 0, S m_z = M_pz + M_z = 0,

где P_x, P_y, P_z - проекции приложенных к отсеченной части стержня внешних сил соответственно на оси x, y, z; M_px, M_py, M_pz - моменты внешних сил относительно осей x, y, z.

Допущение о малости перемещений дает возможность в уравнения (4.15) ввести геометрические параметры (размеры, очертания осей или углы наклона сил и их плечи) недеформированного состояния. Ввиду этого число уравнений равновесия равно числу неизвестных, система является статически определимой. При решении плоской задачи будут иметь место только три внутренних усилия (M, Q, N) и три уравнения равновесия.

Из системы (4.15) следует простой способ вычисления внутренних усилий в любом сечении свободного незамкнутого стержня, загруженного самоуравновешенной нагрузкой. Для этого необходимо провести сечение, рассмотреть любую отсеченную часть стержня и составить соответствующие уравнения равновесия.

Приведенные выше рассуждения показывают, что внутренние усилия представляют собой интегральную характеристику напряженного состояния сечения в целом, в то время как напряжения определяют состояние отдельной точки сечения. Из этих же рассуждений следует, что по известным внутренним усилиям с учетом принятых геометрических гипотез легко могут быть найдены напряжения. Внутренние усилия, таким образом, являются основным инструментом анализа напряженного состояния конструкции. Поэтому задачу вычисления внутренних усилий в строительной механике часто называют основной.

Решение задачи определения внутренних усилий и напряжений принято представлять в виде графиков - эпюр усилий и напряжений. Они показывают значения усилий и характер их изменения по длине каждого элемента сооружения и эпюр напряжений - по сечению. Эпюры дают возможность при соответствующем опыте мгновенно оценить состояние конструкции, увидеть опасные сечения (точки), наметить при необходимости способы перераспределения внутренних усилий.

В анализе напряженно деформированного состояния элементов конструкций задача определения внутренних усилий является наиболее трудоемкой, и хотя все необходимые вычисления при этом полностью основываются на составлении уравнений равновесия, для ее успешного решения требуется иметь прочные практические навыки.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: