 |
Каков порядок расчета статически определимых балок?
|
|
|
|
Наиболее распространенным и простым приемом при определении усилий в балке является расчет ее по отдельным пролетам. Для этого сечениями, близкими к опорам, вырезается отрезок стержня. В соответствии с концепцией сил отброшенные связи заменяются усилиями. К каждому выделенному отрезку стержня (балки) при этом должны быть приложены внешняя нагрузка и усилия в отброшенных связях (поперечные силы и изгибающие моменты по концам). Концевые моменты называют опорными. Определение этих моментов расчетчики считают основным вопросом, который следует решить при нахождении усилий в балках. Чтобы показать, как найти внутренние усилия по известным опорным моментам, разберем расчет простых балок.
Простые балки
П р и м е р 10.1. Дана балка пролетом l = 18 м, загруженная распределенной и сосредоточенной нагрузкой, а также моментами, приложенными к балке вблизи опор (рис.10.10, а1). Требуется построить эпюры распределения внутренних усилий (изгибающих моментов и поперечных сил) вдоль балки.
Р е ш е н и е. Сечениями, близкими к опорам, вырежем отрезок балки (он не включает только точки опирания). Приложим к его концам внутренние усилия. В нашем случае это поперечные силы - Qл и Qп. Так как опоры шарнирные, изгибающие моменты равны нулю. Поперечные силы направим в положительную сторону, то есть так, чтобы они вращали отрезок балки по часовой стрелке.
Из условий равновесия этого отрезка стержня
SmА = 2×9(4.5 + 2) + 12(2 + 9 + 2) + 8 - 21 + Qп × 18 = 0 ,
SmВ = - 2×9(4.5 + 2 + 5) - 12×5 + 8 - 21 + Qл ×18 = 0
найдем поперечные силы
Qп = - 14.4 кН (вектор поперечной силы направлен вверх),
Qл= 15.6 кН.
По известным силам вычислим внутренние усилия в характерных точках и построим графики их распределения вдоль стержня (см. рис. 10.10, а3, а4)
|
|
|
Разобранные примеры показывают, что если основная задача расчета балок - определение опорных моментов - решена, то в пределах каждого пролета можно достаточно просто найти распределение усилий.
Равнопролетные неразрезные балки
Равнопролетные неразрезные балки широко распространены и поэтому хорошо изучены. Имеется широкий набор таблиц по их расчету. По мере удаления от загруженного пролета усилия в балке затухают. Так, уже в третьем пролете опорный момент уменьшается в 15 ¸ 20 раз. Поэтому для расчета балки с любым количеством пролетов практически достаточно иметь решения для балок до пяти пролетов включительно.
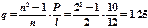 кН/м.
кН/м.
Загружение каждого пролета будем рассматривать в отдельности. В соответствии с табл. 10.2 получим значения опорных моментов
Вычисление пролетных моментов и поперечных сил. Рассмотрим равновесие отрезков балки в пределах каждого пролета. Для этого разрежем балку, сечениями близкими к опорам. В соответствии с концепцией сил к каждому выделенному отрезку стержня (балки) при этом должны быть приложены внешняя нагрузка и усилия в отброшенных связях (поперечные силы и изгибающие момент концам. Значения изгибающих моментов на опорах вычислены и направляются так, чтобы растягивали верхние волокна (моменты отрицательны). По методике, разобранной для простых балок, из условий равновесия находим поперечные силы по концам:
в первом пролете – AB
В каждом пролете по известным поперечным силам с учетом внешней нагрузки и опорных моментов вычислим изгибающие моменты в любом количестве сечений по пролету.
Например, в серединах пролетов:
AB® M BC ® MCD® M
Шарнирно-консольные балки
Обычно шарнирно-консольные балки статически определимы, то есть в них выполняется условие (10.2). В таких балках опорные моменты вычисляются из равенства нулю моментов в шарнирах. В связи с этим расчет балок мало отличается от общей схемы определения усилий в статически определимых системах. Отличия, обусловленные спецификой самих балок, выражаются в том, что для определения опорных реакций и усилий в соединениях балка разбивается по шарнирам. В качестве объектов равновесия выбираются стержни между шарнирами. К ним прикладываются реакции опор и усилия в соединениях, которые при вертикальной нагрузке также вертикальны. Имея в виду то, что для параллельной системы сил (при вертикальной нагрузке в балке возникают только вертикальные реакции) можно составить два независимых уравнения статики, расчет начинается с того элемента, к которому приложены две неизвестные реакции. Одновременное определение реакций в каждом элементе и построение эпюр дает возможность уменьшить погрешности вычислений и проводить простую проверку получаемых результатов.
|
|
|
К шарнирно-консольным балкам можно также применить процедуру, разобранную ранее для простых и неразрезных балок. В пролете с одним шарниром изгибающий момент на одной из опор должен быть известен. Эта опора принимается шарнирной, то есть пролет с одним шарниром преобразуется к пролету с двумя шарнирами и дополнительной нагрузкой в виде сосредоточенного момента, равного опорному.
Построение эпюр внутренних усилий. Значения внутренних усилий удобно вычислять в тех же элементах, которые выбраны в качестве объектов равновесия. Это исключает громоздкие вычисления и уменьшает ошибки.
|
|
|


