Рабочие нагрузки на проектируемый привод

Как следует из исходных данных, объект управления – промышленный робот (ПР) (см. рис. 1.1) с двумя механизмами поворота, осуществляющими поворот руки ПР относительно двух вертикальных осей 1–1 (угол поворота φ₁(t)) и 2–2 (угол поворота φ₂(t)) и механизм подъема руки с зажатым в захватывающем устройстве грузом (поступательное перемещение С₃(t)).

Перемещение по степеням подвижности осуществляется последовательно, поэтому рабочую нагрузку привода, расположенного в центре масс 1-го шарнира и осуществляющего поворот руки на угол φ₁(t), определяют 1-е и 2-е звенья руки ПР с длиной l₁, l₂ и массами m₁, m₂, масса зубчатой рейки m_p, масса захватывающего устройства, указываемая в исходных данных вместе с массой груза m, масса m_n2 привода, осуществляющего поворот ПР на угол φ₂(t), сосредоточенная в центре масс 2-го шарнира и масса m_п3 привода, осуществляющего поступательное перемещение С₃(t), сосредоточенная в центре масс механизма подъема.

Рабочую нагрузку привода, осуществляющего поворот руки ПР на угол φ₂(t), определяет 2-е звено руки с массой m₂, масса зубчатой рейки m_p, масса захвата с грузом m, масса m_п3 привода в механизме подъема.

Рабочую нагрузку привода, осуществляющего подъем руки, определяют масса зубчатой рейки m_p, масса захвата с грузом m.

При определении энергетических параметров проектируемого привода сложную многомассовую нагрузку привода (рис. 3.1) приводят к одному валу – валу двигателя. Для этого много массовую нагрузку с мощностью заменяют маховиком той же мощности на валу двигателя и вращающимся со скоростью вала двигателя [38, §19.3; 20, § II.2]:

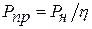, (3.1)

где h – КПД механической передачи от вала нагрузки к валу двигателя.

С другой стороны,

, (3.2)

где 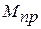– момент приведенной нагрузки к валу двигателя, – момент на валу нагрузки, , – угловые скорости вала двигателя и вала нагрузки, соответственно (см. рис. 3.1), Подставляя (3.2) в (3.1), получаем

,

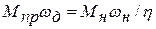откуда

,

где – передаточное отношение механической передачи между валом двигателя и валом нагрузки (передаточное число редуктора).

 

 

Рис. 3.1. Многомассовая нагрузка привода

Моменты, действующие на валу нагрузки, можно разделить на две группы [20, § II.2]. К первой группе относятся динамические моменты , величина которых пропорциональна ускорениям и моментам инерции движущихся масс нагрузки. Ко второй группе относятся моменты статические , связанные с противодействующими усилиями: моменты сухого и вязкого трения, момент статического сопротивления подъему груза.

Таким образом, момент нагрузки, приведенный к валу двигателя,

.(3.4)

Динамические моменты нагрузки приводов

Рассмотрим первый привод, осуществляющий рабочий поворот на угол φ₁(t). Динамический момент нагрузки привода определяется уравнением

,(3.5)

где – ускорение на валу нагрузки; 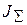– момент инерции нагрузки.

Нагрузка первого привода является телом сложной конфигурации, как уже было показано, поэтому 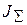определяем как сумму моментов инерции отдельных частей нагрузки относительно оси вращения 1–1. При этом вначале определяют моменты инерции отдельных составляющих нагрузки относительно осей, проходящих через их центры масс и параллельных общей оси вращения, а затем, используя теорему Штейнера:

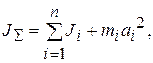
(3.6)

находят момент инерции 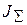сложной нагрузки. Здесь – момент инерции одного элемента нагрузки с массой относительно оси, проходящей через его центр масс, - расстояние от этой оси вращения до общей оси вращения.

В соответствии с конструктивной схемой ПР (см. рис. 1.1), исходными данными и приведенным выше описанием нагрузки приводов момент инерции нагрузки 1-го привода находим по уравнению (3.6):

(3.7)

Динамический момент инерции нагрузки 2-го привода относительно оси вращения 2–2 в соответствии с приведенным выше описанием нагрузки и уравнением (3.6):

(3.8)

Динамический момент нагрузки 2-го привода

(3.9)

Третий привод расположен в механизме подъема 3 (см. рис. 1.1). Привод имеет зубчато-реечную передачу, выполненную в виде зубчатой рейки 5, находящейся в зацеплении с зубчатой шестерней 6 [17, § 7.2]. Вращение от двигателя привода передается через редуктор на шестерню 6, установленную на выходном валу редуктора. Вращательное движение шестерни 6 преобразуется в поступательное перемещение зубчатой рейки 5. Рейку 5 закрепляют на подвижной каретке, которая базируется в корпусе механизма подъема на четырех парах подшипников качения.

Поступательное перемещение С₃(t), скорость рС₃(t) и ускорение р²С₃(t) перемещения рейки связаны с углом поворота j₃(t), угловой скоростью рj₃(t), ускорением р²j₃(t) выходного вала редуктора, на котором установлена шестерня 6. Передаточное отношение зубчато-реечной передачи от выходного вала редуктора к поступательно движущейся рейке:

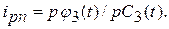(3.10)

Момент инерции нагрузки привода определяется массами m груза и рейки, передаточным отношением [38, § 19.3]:

(3.11)

Динамический момент нагрузки 3-го привода

(3.12)

Масса груза, зажатого в захватном устройстве [12], может меняться в пределах от до , что приводит также к изменению моментов инерции нагрузки и динамических моментов в определенных пределах. При значительных изменениях это обстоятельство существенно влияет на динамические характеристики привода.

Статические моменты нагрузки приводов

 

Статические моменты нагрузки в механизмах поворота невелики [29, § 1.4]. Основной нагрузкой таких механизмов является динамический момент. В механизмах поворота (шарниры 1 и 2) имеется подвижная платформа, на которой закрепляется шестерня [5, глава 1]. Поворот шестерни относительно вертикальной оси (1–1 или 2–2) производится от электродвигателя привода через редуктор и зубчатое колесо, расположенное на выходном валу редуктора. Зубчатое колесо введено в зацепление с шестерней на подвижной платформе.

Движению в механизмах поворота противодействуют статические моменты сопротивления: моменты вязкого и сухого трения, характерные для зубчатых передач механизмов поворота.

Момент вязкого трения пропорционален угловой скорости вала нагрузки и определяется уравнением:

(3.13)

где – коэффициент вязкого трения, зависящий от вязкости и температуры смазывающих масел.

Момент сухого трения в большинстве случаев считают независимым от

 

 

скорости и направленным против нее:

(3.14)

здесь = const.

Согласно (3.13), (3.14), статические моменты нагрузки 1-го и 2-го привода:

(3.15)

(3.16)

Статический момент нагрузки привода в механизме подъема 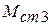обусловлен двумя основными факторами: силами трения в подшипниках качения, на которых базируется подвижная каретка с зубчатой рейкой и силой тяжести груза в захвате. Определяющей силой является сила тяжести. Статическим моментом нагрузки, обусловленным силой трения можно пренебречь. Статический момент нагрузки привода в механизмах подъема может быть очень большим. Отсюда возникло стремление разгрузить привод за счет специальных устройств. Этот способ полной или частичной разгрузки приводов от статических моментов, обусловленных силами тяжести звеньев, называется статическим уравновешиванием. Статическое уравновешивание уменьшает потребную мощность привода, но одновременно усложняет конструкцию механизма подъема.

На практике нашли применение три способа уравновешивания [17, глава 8]: первый способ предлагает установку противовеса, как это делается в двухконцевых лебедках, но это приводит к увеличению момента инерции механизма, а следовательно, к увеличению динамической нагрузки на привод. Второй способ предлагает использовать для статического уравновешивания мощность основного или дополнительного привода механизма. Недостатком такого способа является существенное увеличение мощности привода, но сохраняет высокое быстродействие. В третьем способе используют пружинные уравновешиватели. Но эти уравновешиватели дают неполную компенсацию статических моментов. Достаточно полная компенсация возможна лишь при малых поступательных перемещениях груза. Кроме того, пружинные уравновешиватели имеют низкую надежность при напряженных циклах работы.

В механизме подъема ПР (см. рис. 1.1) использован комбинированный способ статического уравновешивания: с помощью пружинных уравновешивателей компенсируют треть статической нагрузки, а две трети момента остаются нагрузкой привода и определяются уравнением [38, §19.3; 20, § II.3]

(3.17)

где g = 9,81 м/с² – ускорение свободного падения.

 

 

 

 

 

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: