 |
Синтез структуры регулятора
|
|
|
|
В структуре управляемого привода два модуля: силовой (СМ) и управляющий (УМ). В предыдущих разделах методических указаний уже рассмотрены вопросы проектирования и математического описания силового модуля, выбора изме-рителя рассогласований (ИР), принадлежащего управляющему модулю (п. 3.2.1). Вторым блоком УМ является регулятор, синтезу регулятора и посвящается настоящий раздел методических указаний.
Особенностью управляемого привода является невысокий (максимум 4-й) порядок неизменяемой части привода: СМ + ИР. Для систем такого порядка при синтезе регулятора очень хорошие результаты дает простой метод: настройка регулятора на оптимум по модулю ОМ [4, § 1.3.1]. Название метода объясняется тем, что выбираемый регулятор обеспечивает замечательную частотную характеристику системы в замкнутом состоянии: единичный модуль частотной передаточной функции системы в широкой полосе частот. Такая частотная характеристика обеспечивает высокое быстродействие системы и большой запас устойчивости. Регулятор в системе, настроенной на оптимум по модулю, компенсирует влияние на динамику системы большой постоянной времени, оставляя в желаемой структуре лишь малые постоянные времени.
Синтез регулятора управляемого привода, настроенного на ОМ, покажем на примере системы с типовой структурной схемой (рис. 3.7).
Рис. 3.7. Пример структурной схемы системы
Передаточная функция неизменяемой части системы:
.
Соотношение постоянных времени инерционных звеньев системы: 
На рис. 3.8 показана логарифмическая амплитудная частотная характеристика (ЛАЧХ) неизменяемой части системы 
. Как видим из ЛАЧХ (см. рис. 3.8) на динамику работы системы в основном влияет инерционное звено с большой постоянной времени 
, работающее на нижних частотах. Малоинерционные звенья с постоянными времени 
и 
работают в области высоких частот и на динамику системы оказывают незначительное влияние. Для систем с такими частотными характеристиками можно применять метод понижения расчетного порядка [4, § 1.3.3]. Суть метода в замене при расчете системы двух или более звеньев с малыми постоянными времени одним эквивалентным звеном с суммарной постоянной времени. Но метод применим лишь в случае, если полученное эквивалентное звено тоже малоинерционное, т. е. работает в области высоких частот и частота сопряжения эквивалентного звена значительно правее частоты среза системы. На рис. 3.8 на частотной характеристике пунктиром показана замена двух малоинерционных звеньев одним эквивалентным.
|
|
|
При такой замене расчетная передаточная функция неизменяемой части системы:
, (3.49)
где 
, а логарифмическая частотная характеристика на рис. 3.8 обозначена: 
.
Рис. 3.8. Логарифмические амплитудно-частотные характеристики
Расчетная желаемая передаточная функция разомкнутой системы, настроенной на ОМ, для рассматриваемого примера (см. формулу (3.49))
, (3.50)
а логарифмическая частотная характеристика, ей соответствующая, на рис. 3.3 обозначена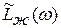 
. Как видим (см. рис. 3.8), в желаемой структуре остается только звено с малой постоянной времени, а компенсация влияния звена инерционного с постоянной времени , является задачей регулятора, настроенного на оптимум по модулю. Передаточная функция регулятора рассчитывается по формуле:
, (3.51)
где 
.
Реальная передаточная функция желаемой системы:
, (3.52)
логарифмическая частотная характеристика, соответствующая желаемой системе, на рис. 3.8 обозначена 
.
Итак: рассматриваемый метод синтеза – настройка регулятора системы на оптимум по модулю позволяет, как следует из расчетов и полученных логарифмических частотных характеристик (см. рис. 3.8), обеспечить высокие добротность привода по скорости и быстродействие, большой запас устойчивости. Время переходного процесса 
, а перерегулирование σ % < 10%. Замечательно то, что структура регулятора всего лишь 1-го порядка, это еще одно неоспоримое достоинство метода.
|
|
|
Если метод понижения расчетного порядка неприменим, расчеты по методу настройки на ОМ дают нереализуемую структуру регулятора. В этих случаях для синтеза структуры управляемого привода следует использовать традиционный метод построения логарифмических частотных характеристик (желаемой и располагаемой) на базе частотных критериев качества [7, § 1.4, 1.5; 8, § 12.6] или любой другой метод, позволяющий найти структуру системы, удовлетворяющую требованиям ТЗ по качеству.
|
|
|
