Систематических погрешностей

 

1. Способ последовательных разностей с использованием критерия Аббе. Этот способ позволяет определить изменяющуюся по времени систематическую погрешность. Для этого необходимо определить дисперсию:

. [1.3]

и сумму квадратов последовательных разностей

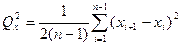. [1.4]

Если в процессе измерений происходило смещение центра группирования результатов наблюдения, т.е. имела место переменная систематическая погрешность, то 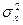дает преувеличенную оценку дисперсии. В то же время изменение центра группирования весьма мало сказываются на значениях разностей , поэтому смещения почти не отражаются на значении 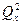. Отношение 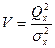является критерием для обнаружения систематических смещений центра группирования результатов наблюдений.

Критерий для этого отношения – критерий Аббе – определяется как , где - уровень значимости, а P – доверительная вероятность. Значения для различных значений q и n - число наблюдений приведены в таблице 1.1. Если , то это значит, что существует систематическая погрешность.

Таблица 1.1

Значения критерия Аббе

n	при q, равном	n	при q, равном
0,001	0,01	0,05	0,001	0,01	0,05
	0,295	0,313	0,390		0,295	0,431	0,578
	0,208	0,269	0,410		0,311	0,447	0,591
	0,182	0,281	0,445		0,327	0,461	0,603
	0,185	0,307	0,468		0,341	0,474	0,614
	0,202	0,331	0,491		0,355	0,487	0,624
	0,221	0,354	0,512		0,368	0,499	0,633
	0,241	0,376	0,531		0,381	0,510	0,642
	0,260	0,396	0,548		0,393	0,520	0,650
	0,278	0,414	0,564

Пример 1.1 Используя способ последовательных разностей, определить, существует ли систематическая погрешность в ряду результатов наблюдений, которые приведены в таблице 1.2.

Таблица 1.2

 

n
	23,6	-	-
	23,8	0,2	0,04	0,2	0,04
	23,7	-0,1	0,01	0,1	0,01
	23,3	-0,4	0,16	-0,3	0,09
	23.4	0,1	0,01	-0,2	0,04
	23,7	0,3	0,09	0,1	0,01
	23,4	-0,3	0,09	-0,2	0,04
	23,6	0,2	0,04
	23,7	0,1	0,01	0,1	0,01
	23,8	0,1	0,01	0,2	0,04
		-		-

 

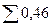
Вычисляем:

1. Среднее значение

2. Значение

3. Дисперсию

4. Критерий Аббе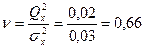

Как видно из таблицы 1.1 для всех уровней значимости при n = 10 получили . Следовательно, подтверждается гипотеза о постоянстве центра группирования, т.е. систематическая погрешность не обнаружена.

2. Дисперсный анализ с использованием критерия Фишера. Данный способ обнаружения систематической погрешности применяется при наличии серий измерений, разделенных между собой или по принципу временной последовательности, или по принципу влияния внешних факторов (температура, напряжение питающей сети и т.д.). Общее число наблюдений N разбивается на S серий (S > 3), в каждой из которых содержится n_j наблюдений, т.е. . Суть анализа состоит в том, что необходимо определить существуют ли систематические отклонения между результатами наблюдения в различных сериях. При этом считается, что колебания результатов наблюдений внутри каждой серии носит случайный характер. Характеристикой этих колебаний является внутрисерийная дисперсия, вычисляемая по формуле:

,

где - среднее значение результатов наблюдений в каждой серии.

В то же время рассеяние в разных сериях может вызываться не только случайными, но и систематическими погрешностями. Характеристикой этих отклонений будет межсерийная дисперсия:

,

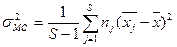где .

Таким образом, отношение характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайных погрешностей, а - долю дисперсии, обусловленную межсерийными различиями результатов наблюдений.

Критерием оценки наличия систематической погрешности в данном случае является критерий Фишера . Значение F_q для различных уровней значимости q, числа измерений N и числа серий S приведены в таблице 1.3, где k₂ = N – S, k₁ = S – 1. Если вычисленное значение критерия Фишера больше F_q, то это значит, что существует систематическая погрешность.

Дисперсионный анализ является наиболее эффективным и достоверным способом обнаружения систематических погрешностей.

 

 

Таблица 1.3

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: