Прямые и многократные равноточные измерения

 

Равноточные измерения – измерения, проводимые СИ одинаковой точности по одной и той же методике при неизменных внешних условиях. При этих измерениях всех серий должны быть равны между собой.

Задача обработки результатов многократных измерений заключается в нахождении оценки измеряемой величины и доверительного интервала, в котором находится ее истинное значение. Информацией для обработки является ряд из n (n > 4) значений, из которых исключены систематические погрешности, т.е. исправленная выборка. Число n зависит от требований к точности результата, так и от возможности выполнять повторные измерения.

Последовательность обработки состоит из ряда этапов.

I этап. Определение точечных оценок закона распределения результатов наблюдения:

- Среднее арифметическое значение ;

- Среднеквадратическое отклонение результата измерений ;

- Среднеквадратическое отклонение среднего значения .

В соответствии с критериями определения грубых погрешностей они исключаются, после чего производится пересчет значений , .

II этап. Определение закона распределения результатов измерений.

Первым шагом при идентификации закона распределения является построение вариационного ряда (упорядоченная выборка, в которой члены ряда располагаются в порядке возрастания). Затем ряд разбивается на оптимальное число m интервалов группирования длиной

,

где 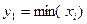и .

Число m определяется в соответствии с рекомендациями, в частности, для практического использования

и ,

где n – число членов ряда.

Число m должно быть нечетным.

 

Второй шаг. Определение интервалов группирования в виде

.

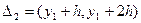
Третий шаг. Определение числа попаданий (частоты) результатов измерений в каждый из интервалов по формуле , где .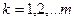

Четвертый шаг. Построение гистограммы и полигона. Для этого по оси абсцисс откладывают интервалы в порядке возрастания номеров (рис. 1.4) на каждом интервале строится прямоугольник высотой 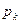. Полигон представляет собой ломаную кривую, соединяющую середины верхних оснований каждого столбца гистограммы. Он более наглядно отражает форму кривой распределения. По форме полигона делается предположение о законе распределения результатов наблюдений.

 

Рис. 1.4. Гистограмма и полигон

 

 

Пятый шаг. Оценка закона распределения по статистическим критериям.

При выборке n > 50 для идентификации закона распределения используют – критерий Пирсона. При 50 > n > 15 для проверки нормальности закона распределения применяется составной критерий (d - критерий). При n < 15 принадлежность экспериментального распределения к нормальному не проверяется.

Идея метода на основе критерия Пирсона состоит в контроле отклонений гистограмм экспериментальных данных от гистограмм с тем же числом интервалов, построенной на основе распределения, совпадение с которым определяется.

Критерий Пирсона вычисляется по формуле

,

где m – число интервалов; n_i – экспериментальное значение частот в i –ом интервале разбиения; P_i – значения вероятностей в том же интервале, соответствующей выбранной модели распределения; .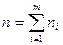

Проверка гипотезы производится сравнением расчетного значения - критерия с табличным , значение которого зависит выбранного уровня значимости q и числа степеней свободы . Для нормального закона распределения z = 2.

Гипотеза о нормальности закона распределения принимается, если .

Шестой шаг. Определение доверительных границ.

Если удалось идентифицировать закон распределения результатов измерения, то с его использованием необходимо найти аргумент функции Лапласа (квантильный множитель) при заданном значении доверительной вероятности P. В этом случае доверительные границы определяются как .

Пример 1.3 50 равноточных многократных измерений u_i, каждое из которых повторилось m раз приведены в графах 1 и 2 таблицы 1.8. Проверить гипотезу о том что результат измерения подчиняется нормальному закону распределения. В случае подтверждения гипотезы определить доверительный интервал.

 

Таблица 1.8.

 

u	m	mu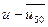
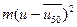
23,3		23,3	-0,36	0,1296	0,1296
23,4		46,8	-0,26	0,0676	0,1352
23,5		164,5	-0,16	0,0256	0,1792
23,6		283,2	-0,06	0,0036	0,0432
23,7		355,5	0,04	0,0016	0,0240
23,8		190,4	0,14	0,0196	0,1568
23,9		95,6	0,24	0,0576	0,2304
24.0		24,0	0,34	0,1156	0,1156
		∑ 1183,3			∑ 1,014

1. Определяем среднее арифметическое значение

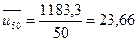
2. Определяем среднеквадратическое отклонение

3. Производим цензурирование выборки, т.е. проверяем наличие значений, выходящих за границы неравенства

.

Ни одно из значений u не выходит за эти пределы, следовательно ошибок (промахов) нет.

4. Построение гистограммы и полигона. Для этого определяем частоты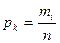

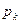
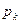
23,3	0,02	23,7	0,3
23,4	0,04	23,8	0,16
23,5	0,14	23,9	0,08
23,6	0,24	24,0	0,02

 

Очертания полигона схожи с дифференциальной функцией нормального закона распределения вероятности. Поэтому вправе выдвинуть гипотезу о соответствии экспериментальных данных этому закону распределения.

5. Составляем таблицу для расчета - критерия Пирсона с учетом того, что в каждом интервале должно быть не менее 5 значений (таблица 1.9).

Таблица 1.9

	Интервалы
	-∞	23,55		- 0,764	- 0,2776	0,2224	- 1,120	0,1128
	23,55	23,65		- 0,069	- 0, 0275	0,2501	- 0,505	0,0204
	23,65	23,75		0,625	0,2340	0,2615	1,925	0,2834
	23,75	23,85		1,319	0,4065	0,1725	- 0,625	0,0453
	23,85	+∞		+∞	0,5	0,0935	0,325	0,0221

 

6. Определяем, на сколько значений отстоит от 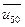граница каждого интервала .

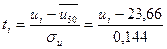
7. Графу 6 заполняем, пользуясь таблицей 1.10 значений функции Лапласа

8. Затем заполняем графу 7, исходя из формулы

Первое значение получаем, зная, что , а последнее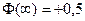

9. Производим вычисление граф 8 и 9. Суммируем все значения 9-ой графы и получаем расчетное значение – критерия Пирсона.

10. Производим сравнение с табличными значениями – критерия (см. таблицу 1.11) при принятом уровне значимости q = 0,1; 0,05; 0,02. Полученные значения меньше любого из них. Следовательно, считаем, что экспериментальное распределение совпадает с теоретическим и гипотеза о нормальном законе распределения вероятности принимается.

Таблица 1.10

Значение функции Лапласа

t
0,0	0,0000	0,0040	0,0080	0,0120	0,0160	0,0199	0,0239	0,0279	0,0319	0,0359
0,1	0,398	0,438	0,478	0,517	0,557	0,596	0,636	0,675	0,714	0,753
0,2	0,793	0,832	0,871	0,910	0,948	0,987
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,5
4,0

 

Таблица 1.11

 

Значение при различном уровне значимости

(критерий Пирсона)

 

ν	при уровне значимости q, равном
0,99	0,95	0,9	0,8	0,5	0,2	0,1	0,05	0,02
	0,02	0,1	0,21	0,45	1,39	3,22	4,61	5,99	7,82
	0,3	0,71	1,06	1,65	3,36	5,99	7,78	9,49	11,67
	0,87	1,63	2,20	3,07	5,35	8,56	10,65	12,59	15,03
	1,65	2,73	3,49	4,59	7,34	11,03	13,36	15,51	18,17
	2,56	3,94	4,87	6,18	9,34	13,44	15,99	18,31	21,16
	3,57	5,23	6,30	7,81	11,34	15,81	18,55	21,03	24,05
	4,66	6,57	7,79	9,47	13,34	18,15	21,06	23,69	26,87
	5,81	7,96	9,31	11,2	15,34	20,46	23,54	26,3	29,63
	8,26	10,85	12,44	14,58	19,34	25,04	28,41	31,41	35,02
	11,52	14,61	16,47	18,94	24,34	30,68	34,38	37,65	41,57
	14,95	18,46	20,60	23,36	29,34	36,25	40,26	43,77	47,96

 

 

11. Определение доверительного интервала при доверительной вероятности P = 0,9.

Зная, что 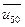=23,66 и = 0,144, получаем

при ; .

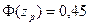Из таблицы функции Лапласа находим аргумент (квантильный множитель).

;

.

Таким образом, с вероятностью P = 0,9 можно считать, что искомый результат находится в границах этого неравенства.

 

 

ОДНОКРАТНЫЕ ИЗМЕРЕНИЯ

Подавляющее большинство измерений являются однократными. В обычных условиях их точность вполне приемлема, а простота, производительность и стоимость ставят их вне конкуренции. В то же время они возможны только при определенных условиях:

- объем априорной информации об объекте измерения таков, что модель объекта и определение измеряемой величины не вызывают сомнения;

- изучен метод измерения, его погрешности или заранее устранены, или оценены в виде поправок;

- СИ исправны, а их метрологические характеристики соответствуют нормированным значениям.

Составляющими погрешности прямых однократных измерений являются:

- погрешности СИ, рассматриваемые по их метрологическим характеристикам;

- погрешность метода измерения, определяемая на основе анализа:

- субъективная погрешность, вносимая оператором.

Если последние две не превышают 15% погрешности СИ, то за погрешность измерения можно принять погрешность СИ.

В общем случае результат однократного измерения может быть представлен единственным значением

,

где - показания отсчетного устройства СИ;

- известное значение поправки.

Однако получение результата зависит от содержания априорной информации. При этом может возникнуть несколько типовых вариантов.

Вариант 1. Отсчет, а следовательно и показания подчиняются нормальному закону распределения вероятности со среднеквадратическим отклонением , а аддитивная поправка равна .

В этом случае результат подчиняется нормальному закону, но смещенному по отношению к закону распределения на величину поправки . По верхней кривой на рис 1.5., задавшись вероятностью P, можно определить величину t, которая показывает на сколько результат измерения может отличаться от среднего значения , равного значению измеряемой величины . Таким образом, с заданной вероятностью

.

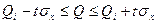Вариант 2. Отсчет подчиняется равномерному закону распределения вероятности с размахом , аддитивная поправка .

В этом случае результат измерения подчиняется равномерному закону с тем же размахом, но смещенному по отношению к закону распределения вероятности показания на значения поправки, т.е.

.

 

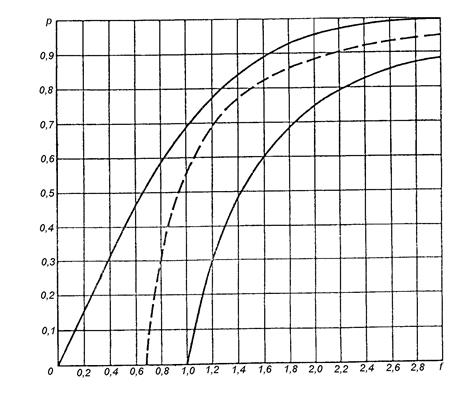
Рис. 1.5. Вероятность попадания значения результата измерения

в окрестность среднего значения

Вариант 3. Отсчет подчиняется неизвестному закону распределения вероятности со среднеквадратическим отклонением , аддитивная поправка - .

Задавшись доверительной вероятностью P, по нижней кривой на рис. 1.5 можно определить на сколько результат отличается от среднего значения результата измерения . Таким образом,

.

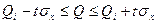Вариант 4. Класс точности СИ таков, что значение измеряемой величины не может отличаться от результата однократного измерения больше на , аддитивная поправка .

Этот вариант не отличается от варианта 2.

Значение измеряемой величины

.

КОСВЕННЫЕ ИЗМЕРЕНИЯ

 

Косвенные измерения – это измерения, при которых искомое значение находят на основании известной зависимости

,

где - значения, полученные прямыми измерениями. По виду функциональной зависимости F они делятся на линейные и нелинейные.

При линейной зависимости связь между измеряемой величиной и аргументами может быть выражена формулой:

,

где - постоянный коэффициент, m – число аргументов.

Погрешность линейных косвенных измерений оценивается методом, основанным на раздельной обработке аргументов и их погрешностей. Для этого получают оценку результатов 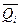на основе многократных прямых измерений.

; ,

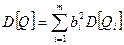где - дисперсия результата.

При нелинейной зависимости погрешность измерения может быть определена по формуле:

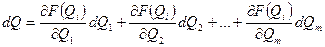
или ,

где 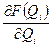- коэффициент влияния.

Если погрешности измерений достаточно малы, то можно заменить дифференциалы 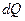, на приращение .

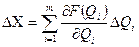
Пример 1.4: Определение погрешности электрического сопротивления проводника длиной l и площадью сечения S.

,

где - удельное электрическое сопротивление.

Более удобно использовать вместо сечения S значение диаметра .

В соответствии с формулой для определения 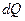запишем

Заменив дифференциалы на приращения, получим

.

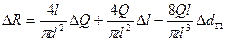Коэффициенты, стоящие перед , , - коэффициенты влияния.

 

СРЕДСТВА ИЗМЕРЕНИЙ

 

Средство измерений (СИ) – техническое устройство, используемое при измерениях и имеющее нормированные метрологические характеристики. СИ также воспроизводит или хранит единицу физической величины, размер которой остается неизменной в течение известного интервала времени. СИ могут реализовывать одну из двух функций:

- воспроизведение величины заданного размера – мера;

- выработка сигнала измерительной информации.

Структура СИ состоит из нескольких элементарных составных частей:

- измерительный преобразователь (датчик) – устройство, построенное на определенном физическом принципе и выполняющее частное измерительное преобразование, т.е. преобразование входного сигнала X в выходной сигнал X₁ (рис. 1.6);

 

Рис. 1.6. Структура средства измерения

 

 

- мера – это СИ, предназначенное для воспроизведения и хранения физической величины одного или нескольких размеров;

- устройство сравнения (компаратор) – это СИ, дающее возможность выполнять сравнение мер однородных величин или же показаний измерительных приборов.

Входным сигналом СИ является измерительный сигнал X, который преобразуется измерительным преобразователем в пропорциональный ему сигнал X₁. Сигнал X₁ поступает на один из входов устройства сравнения, а на второй вход подается известный сигнал X_МС выхода многозначной меры (набор гирь, шкалы, и т.д.). Устройство сравнения дает информацию о том, какое значение выходного сигнала многозначной меры должно быть устранено автоматически или оператором (в простейших случаях). Процесс измерения прекращается при достижении равенства между величинами X₁ и X_М. Выходящий сигнал Y ₁ доступен для восприятия человеком и функционально связан с параметром входного сигнала.

СИ могут работать в двух режимах:

- статическом – режиме, при котором изменением измеряемой величины за время, требуемое для проведения одного измерения, можно пренебречь;

- динамическом – режиме, при котором данным изменением нельзя пренебрегать, т.к. оно превышает допустимую погрешность.

 

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: