Оценка случайных погрешностей

 

Основной постулат метрологии – отсчет (наблюдение, замер) является случайной величиной. В связи с этим результат измерения и его погрешность также могут рассматриваться как случайные величины.

При многократных измерениях одной величины получают совокупность (ряд, серию) наблюдений – случайных величин. Наиболее универсальным способом описания этих величин является интегральная функция распределения F(x) – функция, каждое значение которой для каждого x является вероятностью события, заключающегося в том, что случайная величина в i -ом измерении принимает значение, меньшее x, т.е.

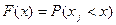
На рис. 1.3а показан график этой функции, изменяющейся от 0 до 1 при изменении x от -∞ до +∞.

На рис. 1.3б показан график дифференциальной функции распределения, который называется также плотностью распределения вероятностей .

Рис. 1.3. Графики интегральной и дифференциальной функций распределения

случайной величины

Вероятность попадания случайной величины в интервал (x₁; x₂):

и равна заштрихованной области, заключенной под кривой p(x) между абсциссами x₁ и x₂.

Использование на практике вероятностных методов предполагает знание аналитических моделей законов распределения. В метрологии встречаются различные модели, вид которых зависит от вида измеряемых величин и используемых приборов.

Множество этих моделей можно классифицировать по группам:

- трапециевидные (плосковершинные);

- уплощенные;

- экспоненциальные;

- семейство распределений Стьюдента;

- двухмодальные распределения.

Наибольшее распределение в метрологии получил нормальный закон распределения – распределение Гаусса.

Это объясняется тем, что распределение случайной погрешности близко к нормальному всегда, когда результаты наблюдений формируются под действием большего числа независимо действующих факторов, каждый из которых оказывает незначительное воздействие по сравнению с суммарным действием всех остальных.

Если ввести переменную , то получится нормированное распределение с интегральной и дифференциальной функциями:

; .

Определенный интеграл:

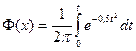
называется функцией Лапласа. Для нее справедливы следующие равенства:

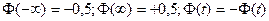
Виды интегральной и дифференциальной функции нормального закона распределения соответствуют изображению на рис 1.3.

 

ТОЧЕЧНЫЕ ОЦЕНКИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ

 

Функции распределения описывают поведение непрерывных случайных величин. На практике результаты измерений и их погрешности являются дискретными величинами. При использовании этих величин возникает задача нахождения точечных оценок функций распределения на основе выборок, т.е. ряда значений x_j, которые должны представлять генеральную совокупность (быть репрезентативной). Оценка является точечной, если она выражается одним числом.

Точечной оценкой математического ожидания результата измерений является среднее арифметическое значение измеряемой величины

. [1.3]

 

Точечная оценка дисперсии

[1.4]

Среднеквадратическое отклонение

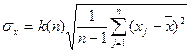, [1.5]

где 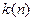- поправочный множитель, зависящий от числа наблюдений и изменяющийся от 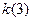= 1,13 до = 1,03.

Полученные оценки и являются случайными величинами, т.к. при повторении серии наблюдений они будут изменяться. Рассеяния этих оценок оценивается с помощью среднеквадратических отклонений и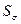

,

 

,

где - эксцесс

На практике из-за небольшого числа наблюдений пренебрегают коэффициентом 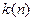и определяют среднеквадратическое отклонение результата измерений:

. [1.6]

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: