Значения критерия Фишера для различных уровней значимости

k2	Fq при k1, равном
									∞
	q = 0,05
	18,51	19,00	19,16	19,25	19,30	19,33	19,37	19,41	19,43	19,50
	7,71	6,94	6,59	6,39	6,26	6,16	6,04	5,91	5,84	5,63
	5,99	5,14	4,76	4,53	4,39	4,28	4,15	4,00	3,92	3,67
	5,32	4,46	4,07	3,84	3,69	3,58	3,44	3,28	3,20	2,93
	4,96	4,10	3,71	3,48	3,33	3,22	3,07	2,91	2,82	2,54
	4,75	3,88	3,49	3,26	3,11	3,00	2,85	2,69	2,60	2,30
	4,60	3,74	3,34	3,11	2,96	2,85	2,70	2,53	2,44	2,13
	4,49	3,63	3,24	3,01	2,85	2,74	2,59	2,42	2,33	2,01
	4,41	3,55	3,16	2,93	2,77	2,66	2,51	2,34	2,25	1,92
	4,35	3,49	3,10	2,87	2,71	2,60	2,45	2,28	2,18	1,64
	4,17	3,32	2,92	2,69	2,53	2,42	2,27	2,09	1,99	1,62
∞	3,84	2,99	2,60	2,37	2,21	2,09	1,94	1,75	1,64	1,00
	q = 0,01
	98,49	99,00	99,17	99,25	99,30	99,33	99,36	99,42	99,44	99,50
	21,20	18,00	16,69	15,98	15,52	15,21	14,80	14,37	14,15	13,46
	13,74	10,92	9,78	9,15	8,75	8,47	8,10	7,72	7,52	6,88
	11,26	8,65	7,59	7,01	6,63	6,37	6,03	5,67	5,48	4,86
	10,04	7,56	6,55	5,99	5,64	5,39	5,06	4,71	4,52	3,91
	9,33	6,93	5,95	5,41	5,06	4,82	4,50	4,16	3,98	3,36
	8,86	6,51	5,56	5,03	4,69	4,46	4,14	3,80	3,62	3,00
	8,53	6,23	5,29	4,77	4,44	4,20	3,89	3,55	3,37	2,75
	8,28	6,01	5,09	4,58	4,25	4,01	3,71	3,37	3,20	2,57
	8,10	5,85	4,94	4,43	4,10	3,87	3,56	3,23	3,05	2,42
	7,56	5,39	4,51	4,02	3,70	3,47	3,17	2,84	2,66	2,01
∞	6,64	4,60	3,78	3,32	3,02	2,80	2,51	2,18	1,99	1,00

Примечание: k ₁- число степеней свободы большей дисперсии; k₂ - число степеней свободы меньшей дисперсии.

Пример 1.2 В таблице 1.4 приведены результаты N = 35 наблюдений в S = 7 сериях по = 5 наблюдений, а также результаты промежуточных вычислений внутрисерийной и межсерийной дисперсии:

 

 

Среднее значение по всем сериям:

Межсерийная дисперсия:

Расчетное значение критерия Фишера:

Определяем табличное значение критерия Фишера при значениях k₁ = S – 1 = 6 и k₂ = N – S = 28 по таблице 1.3 и при уровне значимости q = 0,05, при уровне q = 0,01 F_q будет больше полученного значения F. Следовательно, гипотеза об отсутствии систематической погрешности принимается.

Таблица 1.4

 

Результаты наблюдений	Результаты вычислений
xij   S
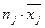
	23,6	23,8	23,7	23,3	23,4	23,56	0,0166	117,8	0,07	0,00245
	23,7	23,4	23,6	23,7	23,8	23,64	0,092	118,2	0,01	0,0005
	23,7	23,7	23,8	23,5	23,7	23,68	0,048	118,4	0,05	0,0125
	23,7	23,6	23,9	23,5	23,7	23,68	0,088	118,4	0,05	0,0125
	23,5	23,7	23,7	23,6	23,6	23,62	0,028	118,1	0,01	0,0005
	23,6	23,6	23,5	23,1	23,7	23,6	0,02	118,0	0,03	0,0045
	23,7	23,9	23,8	23,5	23,8	23,68	0,128	118,4	0,05	0,0125
							∑ = 0,57	∑ = 827,3		∑ = 0,04495

 

3. Способ обнаружения систематической погрешности с использованием статистического критерия Вилкоксона. Этот способ используется в случае отсутствия данных о законе распределения результатов наблюдений.

Производится две группы наблюдений: x₁, x₂,…x_n и y₁, y₂…y_m. При этом .

Все n + m наблюдений располагают в вариационный ряд в порядке возрастания и присваивают каждому из них порядковый номер – ранг.

Различие средних значений ряда можно считать допустимым, т.е. констатировать отсутствие систематической ошибки, если выполняется неравенство

,

где R_i – ранг члена x_j, а и - нижнее и верхнее критические значения для выбранного уровня значимости q. При 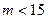критические значения выбираются из таблицы 1.4а, а при рассчитываются по формулам:

 

,

где - аргумент функции Лапласа.

Таблица 1.4а

Критические значения и при q = 0,05 и 0,01

n	m	q = 0,05	q = 0,01

АНАЛИТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ

СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ

 

Применение этих методов возможно, если известны закономерности возникновения погрешностей.

Пример: Определение поправки на температуру выступающего столбика термометрического вещества жидкостного термометра.

,

где - видимый средний коэффициент объемного расширения (для ртути );

n – число градусов в выступающем столбике;

t – температура, показываемая термометром;

- средняя температура выступающего столбика.

 

Пример. Определение погрешности измерения температуры термометром сопротивления при известных значениях погрешностей сопротивления R₀ (сопротивление при ) и температурного коэффициента сопротивления .

Известна зависимость:

,

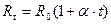где - сопротивление термометра при температуре t.

Связь между погрешностями измерения температуры и сопротивления описывается формулой:

.

Из этой формулы:

.

Погрешность измерения температуры определяется как погрешность косвенного измерения:

;

 

.

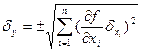⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: