Доверительная вероятность и доверительный интервал

 

Точечные оценки используются, как правило, при значительном числе наблюдений. Чем меньше объем выборки, тем больше возможность ошибки при выборе параметра распределения. Поэтому на практике часто определяют интервал, называемый доверительным, в границах каждого с заданной доверительной вероятностью находится истинное значение оцениваемого параметра

,

где q – уровень значимости; - верхняя и нижняя граница интервала. На практике выбирают значения q = 0,1; 0,05; 0,01.

Для получения интервальной оценки случайной величины по нормальному закону необходимо:

- определить точечную оценку и по формулам [1.3], [1.5];

- выбрать доверительную вероятность p = 1 – q;

- найти верхнюю границу и нижнюю границу 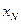интервала с использованием таблиц функции Лапласа .

Полученный доверительный интервал должен удовлетворять условию

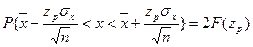
где n – число измерений (объем выборки);

- аргумент функции Лапласа , отвечающий вероятности 0,5 P (квантильный множитель).

Расчет доверительных интервалов для случаев, когда распределение результатов наблюдений нормально, но при малом числе наблюдений (n < 30) возможно выполнять с использованием распределения Стьюдента

где Q – истинное значение измеряемой величины,

- доверительная вероятность, в соответствии с которой по таблице распределения Стьюдента определяется коэффициент .

 

 

ГРУБЫЕ ПОГРЕШНОСТИ И МЕТОДЫ ИХ ИСКЛЮЧЕНИЯ

 

Источником грубых погрешностей являются резкие изменения условий измерения и ошибки оператора (неправильный отсчет показаний СИ, неправильная запись, неожиданные изменения параметров питания СИ и т.д.). Показания СИ с грубыми погрешностями могут существенно не отличаться от «нормальных» отсчетов. Их можно обнаружить или по виду гистограмм или дифференциальных законов распределения. Особую трудность в обнаружении представляют отсчеты, не удаленные от центра распределения на значительное расстояние (предполагаемые промахи). Отбрасывание показаний с грубыми погрешностями, называемое цензурированием выборки, производится с помощью специальных критериев. Для этого необходимо задаться вероятностью того, что сомнительный результат действительно имеет место в данной выборке.

1. Критерий «трех сигм». Этот критерий применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью маловероятен и его можно сосчитать промахом, если 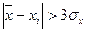. Данный критерий достаточно надежен при числе измерений .

В общем случае границы цензурирования выборки зависят не только от объема выборки n, но и от вида распределения.

2. Критерий Романовского. Этот критерий применяется при объеме выборки n < 20. При этом вычисляется отношение

и сравнивается с критерием , определяется по таблице 1.5.

Таблица 1.5

Значения критерия Романовского

 

q	n = 4	n = 6	n = 8	n = 10	n = 12	n = 15	n = 20
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,64	2,78
0,10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

 

Таблица 1.6

Значения критерия Шарлье

 

n
Kш	1,3	1,65	1,96	2,13	2,24	2,32	2,58

Таблица 1.7

Значения критерия Диксона

 

n	Zq при q, равном
0,10	0,05	0,02	0,01
	0,68	0,76	0,85	0,89
	0,48	0,56	0,64	0,70
	0,40	0,47	0,54	0,59
	0,35	0,41	0,48	0,53
	0,29	0,35	0,41	0,45
	0,28	0,33	0,39	0,43
	0,26	0,31	0,37	0,41
	0,26	0,30	0,36	0,39
	0,22	0,26	0,31	0,34

 

в зависимости от n и q. Если , то результат x_i считается промахом.

3. Критерий Шарлье. Используется при числе наблюдений в ряду n > 20 (таблица 1.6).

4. Вариационный критерий Диксона. Для его расчета результаты наблюдений располагают в вариационный ряд . Расчетное значение критерия

 

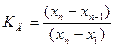
Критическая область для этого критерия

где – табличное значение критерия при уровне значимости q (таблица 1.7).

 

 

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: