Основные термины и определения

МЕТРОЛОГИЯ: ОСНОВНЫЕ ПОНЯТИЯ

Основные термины и определения в области метрологии устанавливаются Рекомендациями по межгосударственной стандартизации РМГ29-99 «Метрология. Основные понятия и определения».

Метрология — наука об измерениях физических величин, методах и средствах обеспечения их единства и способах достижения требуемой точности. В переводе с греческого «метрология» означает учение о мерах. К разделами метрологии относят теоретическую, законодательную и практическую.

1. Теоретическая метрология. Раздел метрологии, предметом которого является разработка фундаментальных основ метрологии.

2. Законодательная метрология. Устанавливаются обязательные технические и юридические требова-ния по применению единиц физических величин, эталонов, методов и средств измерений, направлен-ных на обеспечение единства и необходимой точности измерений в интересах общества.

3. Практическая (прикладная) метрология. Предметом являются вопросы практического применения разработок теоретической метрологии и положений законодательной метрологии.

Измерение физической величины — совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном и неявном виде) измеряемой величины с её единицей и получение значения этой величины.

 

1.1.1. Основные представления теоретической метрологии. Физические величины и единицы.

Согласно РМГ 22-99, физическая величина (ФВ) одно из свойств физического объекта, в качественном отношении общее для многих физических объектов, а в количественном отношении индивидуальное для каждого из них. Величина не существует сама по себе, она имеет место постольку поскольку существует объект со свойствами, выражаемыми определёнными величинами.

Идеальные величины относятся главным образом к математическим абстракциям, являющимися отражением реальности. ФВ присущи материальным объектам и изучаются в курсах естественных (физика, химия) и технических наук. Нефизические величины изучаются в курсах общественных наук - философии, экономике и т.д. Физические объекты обладают неограниченным числом свойств, которые проявляются с бесконечным разнообразием, что вызывает затруднения в их отражении конечными совокупностями чисел, возникающими при их измерении. Отметим, что оценивание нефизических величин не входит в задачи теоретической метрологии. Для более детального изучения ФВ необходимо классифицировать и выявить общие метрологические особенности их отдельных групп.

ФВ целесообразно разделить на измеряемые и оцениваемые. Если первые могут быть выражены количественно в виде определённого числа установленных единиц измерения, то для вторых в силу невозможности введения единицы измерения (твёрдость), приписываются величине определённое число по установленным правилам. Оценивание такой величины осуществляется при помощи шкал.

Шкала величины - упорядоченная последовательность её значений, принятая по соглашению на основании результатов точных измерений.

Нефизические величины могут быть только оценены.

По видам явлений ФВ делятся на следующие группы:

• вещественные, т.е. описывающие физические и физико-химические свойства веществ, материалов и изделий из них. К этой группе относятся масса, плотность, электрическое сопротивление и др. Иногда указанные ФВ называют пассивными. Для их измерения необходимо использовать вспомогательный источник энергии, с помощью которого формируется измерительный сигнал. При этом пассивные ФВ преобразуются в активные, которые и измеряются;

• энергетические, т. е. величины, описывающие энергетические характеристики процессов преобразования, передачи и использования энергии. К ним относятся ток, напряжение, мощность, энергия. Эти величины называют активными. Они могут быть преобразованы в сигналы измерительной информации без использования вспомогательных источников энергии;

• характеризующие протекание процессов во времени. К этой группе относятся различного рода спектральные характеристики, корреляционные функции и др.

По принадлежности к различным группам физических процессов ФВ делятся на пространственно-временные, механические, тепловые, электрические и магнитные, акустические, световые, физико-химические, ионизирующих излучений, атомной и ядерной физики.

По степени условной независимости от других величин данной группы·ФВ делятся на основные (условно независимые), производные (условно зависимые) и дополнительные. В настоящее время в системе СИ используется семь физических величин, выбранных в качестве основных: длина, время, масса, температура, сила электрического тока, сила света и количество вещества. К дополнительным физическим величинам относятся плоский и телесный углы.

По наличию размерности ФВ делятся на размерные, т. е. имеющие размерность, и безразмерные.

Совокупность чисел Q, отображающая различные по размеру однородные величины, должна быть совокупностью одинаково именованных чисел. Это именование является единицей ФВ или ее доли. Условно за единицу принимается физическая величина (ФВ) фиксированного размера, а результат может быть выражен в единицах ФВ или её долях.

Для третьей группы числовое значение показывает, в каком соотношении значение измеряемой величины находится в сравнении с принятым за единицу.

Измерение - познавательный процесс, заключающейся сравнении путём физического эксперимента данной ФВ с известной ФВ, принятой за единицу измерения.

 

1.1.2. Шкалы измерений.

В соответствии с логикой проявления свойств различают 5 основных типов шкал измерений.

1. Шкала наименований (шкала классификации). Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности (атлас цветов). Эти свойства нельзя считать физическими величинами, поэтому это не шкалы ФВ. В шкалах наименований отнесение к классу эквивалентности того или иного отражаемого свойства происходит с использованием органов чувств человека и наиболее адекватен результат, выбранный большинством экспертов. Числа, приписанные объектам, могут быть используемы лишь для определения вероятности или частоты появления объекта, но для математических действий (например суммирования) эти числа использовать нельзя. В таких шкалах нет понятия нуля, “больше“ или “меньше“ и единицы измерения.

2. Шкала порядка (шкала рангов). Если свойство объекта проявляется в отношении эквивалентности и порядка, то можно построить шкалу. При этом в шкале может существовать 0 или нет, но принципиально нельзя ввести единицу измерения. В тех случаях, когда уровень познания не позволяет точно установить отношения, существующие между величинами данной характеристики, используют условные (эмпирические) шкалы порядка. Иногда использование такой шкалы удобно и достаточно для практики. Условная шкала - это шкала ФВ, исходные значения которой выражены в условных единицах (12-бальная шкала Бофорта для силы морского ветра).

Широкое распространение получили шкалы порядка с реперными точками на них (например, шкала твёрдости Мооса). На ней принимается твёрдость талька за 1 (первая реперная точка), гипса за 2, и т.д., алмаза за 10. Отнесение минерала к той или иной градации твёрдости производится на основании эксперимента, когда исследуемый материал царапается опорным. Более твёрдый материал оставит след на образце, значит верхняя граница твёрдости не меньше твёрдости опорного материала. Нижняя граница определяется аналогично.

В условных шкалах одинаковым интервалам между размерами данной величины не соответствуют одинаковые размерности чисел, отображающие размеры. Для вычисления вероятностей эти числа можно использовать, однако их нельзя использовать для других математических операций.

Определение значения величин при помощи таких шкал нельзя считать измерением, т.к. как на такой шкале не может быть введена единица измерения. Это операция оценивания, неоднозначная и весьма условная.

3. Шкала интервалов (шкала разностей). Эта шкала применяется для объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности. Она состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. К таким шкалам относится летоисчисление по различным календарям, температурные шкалы Цельсия, Фаренгейта, Реомюра. На ней определены действия сложения, однако складывать даты событий, например, бессмысленно. Шкала интервалов величины Q описывается уравнением:

Q = Q₀ + q [Q],

где q - числовое значение величины; Q₀ - начало отсчета шкалы;[Q] - единица рассматриваемой величины. Задать шкалу можно двумя способами.

При первом выбирают два значения Q₁ и Q₀ - величины, называемые основные реперы, которые просто реализуются практически, а интервал (Q₁ - Q₀) - называется основной интервал. Точка Q₀ принимается за начало отсчёта, а величина (Q₁ - Q₀)/n = [Q] - за единицу Q.

Перевод одной шкалы интервалов Q = Q₀₁ + q₁[Q]₁, в другую Q = Q₀₂ + q₂ [Q]₂ осуществляется по формуле:

q₂ =(q₁ – )

По второму пути единица воспроизводится как интервал, его доля или некоторое число интервалов, а начало отсчета выбирается каждый раз по - разному, в зависимости от конкретных условий изучаемого явления. Пример такого подхода - шкала времени., в которой секунда равна 9192631770 периодам излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия - 133. За начало отсчета принимается начало изучаемого явления.

4. Шкала отношений. Эти шкалы описывают свойства эмпирических объектов, которые удовлетво-ряют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода - аддитивные), а иногда и пропорциональности (шкалы первого рода - пропорциональные). Примеры: шкала массы (второго рода), термодинамической температуры (первого рода).

В шкалах отношений существует однозначный естественный критерий нуля и единица измерений, установленная по соглашению. Формально шкала отношений - это шкала интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерении ФВ. Шкалы отношений - самые совершенные. Они описываются уравнением:

Q = q [Q],

где Q - ФВ, для которой строится шкала, [Q] - ее единица измерения, q - числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением

q₂ = q₁ [Q]₁ /[Q]₂.

5. Абсолютные шкалы. Иногда используют понятие абсолютных шкал, под которыми понимают шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящее от принятой системы единиц измерения. Такие шкалы соответствуют относительным величинам: коэффициенту усиления и т.д. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.

Шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений - метрическими (материальными). Абсолютные и метрические шкалы относятся к разряду линейных. На практике шкалы измерений стандартизуются, также, как и единицы измерений. В необходимых случаях принимается стандарт способа и условий их однозначного воспроизведения.

Во всех случаях проведения измерений, независимо от измеряемой величины, метода и средства измерений, общее, что составляет основу измерений - сравнение опытным путём данной величины с другой ей подобной, принятой за единицу. Это может быть записано в виде общего уравнения измерений:

Q=n×[Q],

где Q − измеряемая физическая величина; п − число единиц; [Q] − единица физической величины.

Значение физической величины Q, найденное при измерении, называют действительным.

В ряде случаев нет необходимости определять действительное значение физической величины, а достаточно определить принадлежность физической величины некоторой области Т: или .

Контроль - это оценка соответствия физической величины установленному допуску.

Средство измерений (СИ) - это техническое средство, используемое при измерениях и имеющее нормированные метрологические свойства. Для подтверждения этих свойств служит поверка.

Поверка средств измерений – это совокупность операций, выполняемая органами государственной метрологической службы с целью подтверждения соответствия средств измерения установленным техническим требованиям.

Существует огромное количество видов средств измерений, отличающихся по назначению, принципу действия, пределам измерений, точности. Поэтому в метрологии средства измерений классифицируются по определенным признакам.

Средства измерения делятся на:

· эталоны;

· меры;

· образцовые средства;

· рабочие средства.

Эталоны — средства измерений, официально утвержденные и обеспечивающие хранение и воспроизведение единицы физической величины с целью передачи ее размера другим средствам измерений.

Меры — средства измерений, предназначенные для воспроизведения заданного размера физической величины.

Образцовые средстваизмерения — применяютсядля поверки по ним других средств измерений. Это могут быть как меры, так и приборы и инструменты.

Рабочие средства применяют для технических измерений, не связанных с передачей размера единиц

Погрешность - отклонение результата измерения от истинного значения измеряемой величины.

Точность измерений характеризуется близостью их результатов к истинному значению измеряемой величине.

Истинное значение физической величины - это идеализация свойства объекта, не зависящее от средств познания и являющееся абсолютной истиной, к которой мы стремимся, пытаясь выразить в виде числа.

Действительное значение физической величины - значение, найденное экспериментально, и настолько близкое к истинному, что может быть использовано вместо него.

Принцип измерений - физическое явление или совокупность физических явлений, положенных в основу измерений.

Метод измерений - совокупность приёмов использования принципов и средств измерений.

Метод измерения должен по возможности иметь минимальную погрешность и способствовать исключению систематических погрешностей или переводу их в разряд случайных.

Методы измерений

Классификация методов измерений по структурным элементам измерительных операций важна для измерительной техники, метрологии информационно-измерительных систем и отражает тенденции развития микропроцессорной и вычислительной техники. Мы более подробно остановимся на традиционном подходе в силу его большей общности и важности.

Как следует из определения метода измерений, он включает в себя как приёмы измерения, так и технические средства (средства измерения).

По физическому принципу, положенному в основу измерений все методы делятся на электрические, магнитные, акустические, оптические и т.д.

Режим взаимодействия средства и объекта измерений может быть статическим и динамическим.

Третьим признаком может служить применяемый в средствах измерения вид измерительных сигналов: аналоговый и цифровой.

По совокупности приемов использования принципов и средств измерений выделяют:

· метод непосредственной оценки

· метод сравнения.

По сути это непосредственное или опосредованное сравнение с мерой, которое может быть как во времени, так и в отношении физической природы измеряемых величин.

Сущность метода непосредственной оценки состоит в том, что о значении физической величины судят по показанию одного (прямые измерения) или нескольких (косвенные измерения) средств измерения, которые проградуированы в единицах измеряемой величины или единицах других величин, от которых они зависят. Это наиболее распространенный метод измерения. Измерения с помощью этого метода проводятся быстро, просто и не требуют высокой квалификации оператора, поскольку не надо создавать специальные измерительные установки, выполнять сложные вычисления. Однако точность измерений чаще всего оказывается невысокой из-за погрешностей, связанных с необходимостью градуировки шкал приборов и воздействием влияющих причин. Простота метода способствует его автоматизации, что особенно важно при контроле качества продукции и поверке средств измерений.

Другую группу образуют методы сравнения:

· дифференциальный;

· нулевой;

· совпадений;

· замещения.

При дифференциальном методе измеряемая величина сравнивается прямо или косвенно с величиной, воспроизводимой мерой и судят о значении искомой величины по измеряемой прибором разности. Эта разность не уравновешивается и является искомой. Дифференциальный метод позволяет получить весьма точный результат, если измеряемая величина и величина, воспроизводимая мерой, мало отличаются друг от друга. Пример применения ― измерение вольтметром разности двух напряжений, из которых одно известно с большой точностью, а другое представляет собой искомую величину.

Нулевой метод является разновидностью дифференциального, с тем отличием, что результирующий эффект сравнения сводится до нуля, и этот процесс контролируется измерительным прибором высокой точности – нуль – индикатором. Пример нулевого метода – взвешивание на весах.

Метод замещения заключается в поочередном измерении прибором искомой величины и выходного сигнала меры, однородной с измеряемой величиной. Наибольшая точность при этом получается при одинаковых показаниях прибора. Пример – измерение большого активного сопротивления путем поочередного измерения силы тока, протекающего через контролируемый и образцовый резисторы.

При методе совпадений разность между измеряемой величиной и величиной, воспроизводимой, мерой, определяют, используя совпадение отметок шкал или периодических сигналов. Примером может служить измерение длины при помощи штангенциркуля с нониусом. Частота вращения тела таким же методом измеряется посредством стробоскопа.

Классификация измерений

Разделение измерений на группы диктуется потребностями теории и практики и обусловлено удобствами при разработке методик выполнения измерений и обработке результатов.

Наибольшее распространение получила классификация по общим приемам получения результатов измерений. Согласно этому признаку, измерения делятся на:

· прямые;

· косвенные;

· совместные;

· совокупные.

Прямыми называются измерения, при которых искомое значение находят непосредственно по показаниям СИ. Математически прямое измерение может быть представлено в виде уже приводившейся формулы общего уравнения измерений. Числовое значение n, характеризующее разряд величины Q, выраженной в единицах [Q], определяется непосредственно по показаниям мер или измерительных приборов, предназначенных для.измерений данной величины Q.

Например, масса, измеряемая при помощи весов.

Косвенные измерения - это измерения, при которых значение измеряемой величины находят на основании известной зависимости между ней и величинами, получаемыми из прямых измерений, проводимых в одинаковых условиях. Косвенное измерение можно выразить уравнением

Y=f(,

где Y — измеряемая величина; − величины, определяемые из прямых измерений.

Вид связи между Y и 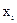определяет методику расчета погрешности косвенных измерений. Для современных измерительно-вычислительных систем, позволяющих сразу вычислять искомую измеряемую величину, результат определяется способом, характерным для прямых измерений. Погрешность измерения входит в нормативно-техническую документацию системы. К косвенным относятся только такие измерения, при которых расчет производится вручную или автоматически, но после получения результатов прямых измерений. Погрешность расчета также может быть отдельно учтена. В измерительных системах, у которых нормированы метрологические характеристики компонентов по отдельности, суммарная погрешность измерений рассчитывается по нормированным метрологическим характеристикам всех компонентов системы.

Совокупными называются проводимые одновременно измерения нескольких одноименных величин, при которых их искомые значения находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.

Совместными называются проводимые одновременно измерения двух или нескольких неодноименных величин для установления зависимости между ними.

В обоих последних случаях искомые значения находятся в результате решения системы уравнений, коэффициенты в которых получены путем прямых измерений. Отличие - в определении одноименных величин (в совокупных измерениях) и разноименных (в совместных).

В зависимости от числа измерений в серии различают:

· однократные;

· многократные.

Однократное измерение — измерение, выполняемое один раз. Например, определение времени по часам. Если необходима большая уверенность в получаемом результате, то проводятся многократные измерения, результат которых получают из нескольких следующих друг за другом измерений. За результат многократного измерения обычно принимают среднее арифметическое значение из результатов однократных измерений, входящих в ряд.

По отношению к изменению измеряемой величины:

· статические;

· динамические.

По выражению результата измерений:

· абсолютные;

· относительные.

При абсолютном измерении результат выражается в узаконенных единицах.

12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: