Прямые многократные неравноточные измерения и обработка их результатов.

Часто проводятся неравноточные измерения одной и той же физической величины: с различной точностью, либо разными приборами в различных условиях, разными исследователями и т.д.

Пусть имеются m серий равноточных измерений объемом n_i, СКО серии и среднее i-й серии. Тогда [2] наиболее вероятным значением величины будет средневзвешенное:

Пределы равноточных измерений определяются в соответствии методом в разделе 1.2.1.

Однократные измерения и обработка их результатов.

Прямые многократные измерения в большой мере относятся к лабораторным измерениям. Для производственных процессов более характерны однократные измерения. Это самые массовые измерения. Однократные измерения возможны, если объем априорной информации такой, что модель объекта и определение измеряемой величины не вызывают сомнений, погрешности метода изучены либо устранены, средства измерения исправны и их метрологические характеристики соответствуют нормам.

За результат прямого однократного измерения принимается полученная величина. До измерения должна быть проведена априорная оценка составляющих погрешности. При определении доверительных границ погрешности результата измерений доверительная вероятность принимается равной, как правило, 0,95.

Условия применения:

· составляющие погрешности известны;

· случайные составляющие распределены по нормальному закону;

· неисключенные систематические заданы своими границами q_i и распределены равномерно.

Составляющими погрешности прямых однократных измерений являются:

· погрешности СИ, рассчитываемые по метрологическим характеристикам;

· погрешность метода измерений, определяемая на основе анализа в каждом конкретном случае;

· личная погрешность, вносимая конкретным оператором.

Если последние две составляющие не превышают 15% погрешности СИ, то остается только одна.

При наличии нескольких систематических погрешностей, заданных своими границами ±q_i, доверительная граница результата измерения может быть вычислена соответственно вышеописанной процедуре:

q(Р) = k 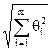(1).

Однократные измерения достаточны, если НСП (например, класс точности СИ) заведомо больше случайной погрешности измерений, т.е. > 8.

В случае, когда < 8 существенную роль играет случайная составляющая и однократные измерения недопустимы.

Если имеет место случай 0,8 ≤ ≤ 8, то погрешность результатов измерения находят по эмпирической формуле:

= ].

Коэффициент 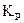находят в таблицах [1-3]. Он зависит от соотношения и доверительной вероятности P. Для P = 0.95 его можно взять из табл.

Табл. 2

 

q/Sx	0,8
K0,95	0,76	0,74	0,71	0,73	0,76	0,78	0,79	0,8	0,81

 

Однократные измерения c приближенным оцениванием результатов.

Прямые однократные измерения с приближенным оцениванием погрешностей правомочны, если доказана возможность пренебрежения случайной составляющей погрешности измерения, т.е. среднее квадратическое отклонение S_x случайной составляющей меньше 1/8 суммарной границы неисключенных систематических составляющих погрешности результата измерения.

В простейшем случае, когда влияющие величины соответствуют нормальным условиям, погрешность результата прямого однократного измерения равна пределу основной погрешности средства измерения D_си, определяемой по нормативно-технической документации.

Результат измерения записывается как D =±D_си Доверительная вероятность не указывается, но, как правило, она равна 0,95. Если условия отличны от нормальных, необходимо учитывать пределы дополнительной погрешности.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: