 |
Обработка результатов косвенных измерений.
|
|
|
|
Косвенные измерения − это измерения, при которых искомое значение A находят на основании известной функции  , где
, где  − значения, полученные при прямых измерениях. Их обработка и представление результатов проводятся в зависимости от наличия или отсутствия связи (корреляции) при проведении этих измерений.
− значения, полученные при прямых измерениях. Их обработка и представление результатов проводятся в зависимости от наличия или отсутствия связи (корреляции) при проведении этих измерений.
Подход к решению задачи нахождения результата косвенных измерений заключается в разложении функции f (достаточно гладкой) в ряд Тейлора в окрестности  [1-3] и учете только членов первого порядка малости.
[1-3] и учете только членов первого порядка малости.
Оценка результата косвенного измерения:
 ,
,
где  − оценка результата i − го аргумента.
− оценка результата i − го аргумента.
Оценка СКО случайной погрешности S( ) результата косвенного измерения вычисляется по формуле:
) результата косвенного измерения вычисляется по формуле:
S(  ) ≈
) ≈ 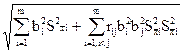 ,
,
где -1 <  < 1 − оценка коэффициента корреляции между погрешностями аргументов
< 1 − оценка коэффициента корреляции между погрешностями аргументов  и
и 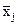 ;
;
 − так называемые коэффициенты влияния i − го аргумента.
− так называемые коэффициенты влияния i − го аргумента.
Корреляция между аргументами чаще всего возникает тогда, когда их измерения проводятся одновременно и подвергаются одинаковому влиянию внешних условий: температуры, влажности, помех и т.д. Точное определение  обычно затруднено [1-3]. Часто рассматриваются случаи, когда имеется полная статистическая связь
обычно затруднено [1-3]. Часто рассматриваются случаи, когда имеется полная статистическая связь  = 1 и ее полное отсутствие
= 1 и ее полное отсутствие  = 0.
= 0.
При отсутствии корреляционной связи между аргументами СКО результата косвенного измерения S(  ), обусловленного случайными погрешностями, вычисляется по формуле:
), обусловленного случайными погрешностями, вычисляется по формуле:
S(  ) =
) =  ,
,
где  − среднее квадратическое отклонение результата измерения аргумента
− среднее квадратическое отклонение результата измерения аргумента 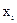 , рассчитанное по формуле
, рассчитанное по формуле  = S
= S  /
/  =
= 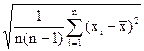 , а
, а  − число измерений i− го аргумента.
− число измерений i− го аргумента.
Для случая косвенного измерения при линейной зависимости между аргументами:
 =
= 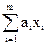 ,
, 
где  − постоянный коэффициент i− го аргумента, m − число аргументов.
− постоянный коэффициент i− го аргумента, m − число аргументов.
|
|
|
S(  ) =
) =  ,
,
Если  = k
= k  , и k,
, и k,  − константы, то определив частные производные по
− константы, то определив частные производные по 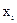 , подставив их в формулу для S(
, подставив их в формулу для S(  ) и разделив полученное выражение на
) и разделив полученное выражение на  , получим:
, получим:
 =
=  =
=  .
.
Здесь  и
и  − относительные среднеквадратичные отклонения случайных погрешностей результата измерения
− относительные среднеквадратичные отклонения случайных погрешностей результата измерения  и i− го аргумента
и i− го аргумента
Обычно считается, что случайные величины распределены по нормальному закону.
При большом числе измерений (более 25-30) выполненных при нахождении каждого аргумента, доверительную границу случайной погрешности результата косвенного измерения определяют по формуле
e(P) = zp S(  ),
),
здесь zp – квантиль нормального распределения, соответствующий выбранной доверительной вероятности Р.
При меньшем числе измерений используется распределение Стьюдента, число степеней свободы которого рассчитывается по приближенной формуле:
k = 
 ,
,
где ni - число измерений при определении аргумента 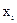 . В этом случае доверительная граница случайной погрешности результата косвенного измерения
. В этом случае доверительная граница случайной погрешности результата косвенного измерения
e(P) = tpS(  ),
),
где tp - коэффициент Стьюдента, соответствующий доверительной вероятности Р = 1-q и числу степеней свободы k.
Систематическая погрешность результата косвенного измерения определяется систематическими погрешностями результатов измерений аргументов. При измерениях их стараются исключить. До конца это сделать не удается; всегда остаются неисключенные систематические погрешности, которые рассматриваются как реализации случайной величины, имеющей равномерное распределение. Доверительные границы неисключенной систематической погрешности результата косвенного измерения q(Р), в случае, когда неисключенные систематические погрешности аргументов заданы границами qi равны:
q(Р) = k 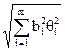
где k - поправочный множитель, определяемый принятой доверительной вероятностью Р и числом m составляющих qi.Его значения приведены в таблице.
Значения коэффициента k при m > 4
|
|
|
Табл. 3
| P | 0,90 | 0,95 | 0,98 | 0,99 |
| k | 0,95 | 1,1 | 1,3 | 1,4 |
Если число суммируемых слагаемых m£ 4 и они значительно различаются между собой, то значение коэффициента k следует взять из [1-3].
Суммарная погрешность результата косвенного измерения оценивается на основе композиции распределений случайных и неисключенных систематических погрешностей, приведенных в следующей таблице.
Табл. 4
Значение q(Р)/ 
| Погрешность результата измерения D(Р) |
q(Р)/  < 0,8 < 0,8
| e(Р) |
0,8 £ q(Р)/  £ 8 £ 8
| kp[e(Р)+q(P)] |
q(Р)/  > 8 > 8
| q(P)] |
Коэффициент для доверительной вероятности P = 0,95 kp определяется по табл
Табл. 5
q(Р)/ 
| 0,5 | 0,75 | ||||||||
| k0,95 | 0,81 | 0,77 | 0,74 | 0,71 | 0,73 | 0,76 | 0,78 | 0,79 | 0,80 | 0,81 |
Результат косвенного измерения записывается в виде х ± D(Р) при доверительной вероятности Р.
ВЫБОР СРЕДСТВ ИЗМЕРЕНИЙ
При выборе СИ учитывают совокупность метрологических (цена деления, погрешность, пределы измерений, измерительное усилие), эксплуатационных и экономических показателей, к которым относятся: массовость (повторяемость измеряемых размеров) и доступность их для контроля; стоимость и надежность СИ; метод измерения; время, затрачиваемое на настройку и процесс измерения; масса, габаритные размеры, рабочая нагрузка; жесткость объекта контроля, шероховатость его поверхности; режим работы и т. д.
Основная трудность технико-экономического подхода при выборе СИ заключается в том, что сам процесс измерения не сопровождается непосредственным созданием материальных ценностей. Учитывая также различные цели контрольно-измерительных операций и их различную принадлежность к этапам жизненного цикла ТС (производство, эксплуатация, ремонт), невозможно предложить единую методику выбора СИ.
Общие принципы выбора на основании накопленного опыта сводятся к следующим положениям:
І. Для гарантирования заданной или расчетной относительной погрешности измерения относительная погрешность СИ должна быть на 25-30% ниже, чем δИ (т. е. δСИ = 0,7 δИ). Если известна приведенная погрешность измерения, то приведенная погрешность СИ:
 ,
,
где xи Xн - результат измерения и нормированное значение шкалы СИ.
ІІ. Выбор СИ зависит от масштаба производства или количества находящихся в эксплуатации однотипных ТС. пример, в массовом производстве с отработанным технологическим процессом, включая контрольные операции, используют высокопроизводительные механизированные и автоматизированные СИ. Универсальные СИ применяются преимущественно для наладки оборудования.
|
|
|
В серийном производстве основными средствами контроля должны быть жесткие предельные калибры, шаблоны, специальные контрольные приспособления. Возможно применение универсальных СИ.
В мелкосерийном и индивидуальном производстве основными являются универсальные СИ, поскольку применение других организационно и экономически невыгодно: неэффективно будут использоваться специальные контрольные приспособления или потребуется большое количество калибров различных типоразмеров.
ІІІ. Метод измерения, определяемый целью контроля, выдвигает требования к СИ по базировке: если контролируется точность технологического процесса, то выбирают СИ для технологических баз; если ТС контролируется с точки зрения эксплуатации, то СИ выбирается под эксплуатационные базы.
IV. При выборе СИ по метрологическим характеристикам необходимо учитывать следующее:
– если технологический процесс неустойчив, т. е. возможны существенные отклонения измеряемого параметра за пределы поля допуска, то нужно, чтобы пределы шкалы СИ превышали диапазон рассеяния значений параметра;
– цена деления шкалы должна выбираться с учетом заданной точности измерения. Например, если размер необходимо контролировать с точностью до 0,01 мм, то и СИ следует выбирать с ценой целения 0,01 мм, так как СИ с более грубой шкалой внесет дополнительные субъективные погрешности, а с более точной - выбирать не имеет смысла из-за удорожания СИ. При контроле технологических процессов должны использоваться СИ с ценой деления не более 1/6 допуска на изготовление;
– поскольку качество измерения определяется величиной относительной погрешности δ= ±(Δ/х) 100%, т. е. с уменьшением х величина δ увеличивается (качество измерения ухудшается). Следовательно, качество измерений на разных участках шкалы неодинаково. Поэтому при измерениях рабочий участок шкалы СИ должен выбираться по правилу: относительная погрешность в пределах рабочего участка шкалы СИ не должна превышать приведенную погрешность более чем в 3раза (δ<3γ). Из этого правила следует:
|
|
|
а) при односторонней равномерной шкале с нулевой отметкой в ее начале рабочий участок занимает последние две трети длины шкалы;
б) при двусторонней шкале с нулевой отметкой посредине последнюю треть каждого сектора;
в) при шкале без нуля рабочий участок может распространяться на всю длину шкалы.
В пределах рабочего участка шкалы наибольшая возможная абсолютная погрешность равновероятна на всех отметках. Таким образом, при выборе СИ важно определить рабочий участок шкалы и ее цену деления. Последняя зависит от класса точности СИ и числа nш делений шкалы.
Если класс точности СИ определяет наибольшую допустимую погрешность с заданной вариацией, то цена деления должна учитывать эту вариацию, а именно - должна быть равна удвоенному значению приведенной погрешности СИ: С= 2γ или nш = 100/2γ.
Исходя из требований удобства считывания показаний, допускается использование более крупных делений шкалы, но обязательно кратных пш (в пределах 2-10). Кроме того, цена деления должна составлять целое число единиц измеряемой величины 1, 2, 5, 10 и т. д.).
|
|
|


