Систематические погрешности

Систематическая погрешность - составляющая погрешности, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же физической величины. Величина систематической погрешности может быть предсказана, и, благодаря этому, в идеале полностью устранена введением соответствующей поправки.

По зависимости абсолютной погрешности от значений измеряемой величины они делятся на:

· аддитивные D_а, не зависящие от измеряемой величины;

· мультипликативные D_м, прямо пропорциональные измеряемой величине;

· нелинейные D_н, имеющие нелинейную зависимость от измеряемой величины.

Аддитивные или постоянные погрешности− погрешности, длительное время сохраняющие свое значение. Они встречаются наиболее часто. К постоянным относятся погрешности большинства мер (гирь, концевых мер длины), погрешности градуировки шкал измерительных приборов и др.

Мультипликативные или прогрессивные погрешности− непрерывно возрастающие или убывающие погрешности. К ним относятся изменение коэффициента усиления усилителя, изменение жесткости пружины прибора, постепенное падение напряжения источника тока и др.

Как один из примеров нелинейных погрешностей можно привести периодические погрешности − погрешности, периодическиизменяющие значение и знак. Обычно такие погрешности встречается в угломерных приборах с круговой шкалой.

Составляющими систематической погрешности являются:

· инструментальная;

· методическая;

· субъективная;

· из-за изменения условий измерений.

Инструментальная погрешность 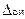− составляющая погрешности измерений, обусловленная погрешностью применяемого СИ. Данная погрешность условно отнесена к систематическим погрешностям СИ, так как она может быть обусловлена действием различных факторов, среди которых могут преобладать и случайные и систематические.

В паспорте СИ указывается максимальное значение инструментальной погрешности. Если СИ имеет несколько диапазонов измерений, погрешность может быть указана для каждого диапазона.

Погрешность метода измерений − составляющая систематической погрешности, обусловленная несовершенством метода измерений (иногда эту погрешность называют теоретической). Погрешность Отличие принятой модели свойств объекта измерений от истинной, упрощения уравнений, описывающих явление, приводят к погрешностям измерений. Для компенсации приходится вводить поправки. Погрешность метода иногда называют теоретической погрешностью. Эта погрешность определяется методикой выполнения измерений.

Субъективная погрешность (погрешность отсчета) 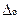− составляющая систематической погрешности измерений, обусловленная индивидуальными способностями оператора. Эта погрешность может появиться в результате отсчета оператором показаний СИ, что вызывается несовершенством органов чувств, эргономическими свойствами средства измерения и т.п.

Погрешность из-за изменения условий измерений − составляющая систематической погрешности измерений, являющаяся следствием неучтенного влияния отклонения какого-либо из параметров, характеризующих условия измерений, от установленных значений. Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля в месте измерений, вибрации и др.); неправильной установки СИ, нарушения правил их взаимного расположения и т.п.

Для оценки влияния систематических погрешностей на результат измерения применяется неисключенная систематическая погрешность

Неисключенная систематическая погрешность (НСП) – составляющая погрешности результата измерений, обусловленная погрешностями вычислений и введения поправок на влияние систематических погрешностей, или систематической погрешностью, поправка на которую не введена вследствие её малости. Иногда этот вид погрешности называют неисключенным остатком систематической погрешности. Неисключенная систематическая погрешность характеризуется ее границами. Границы НСП при числе составляющих m≤3 определяются по формуле:

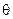(P) = .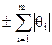

где 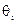– граница i – ой составляющей НСП. При большем числе составляющих погрешности вычисления проводят по формуле:

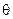(P) = k .

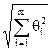при P = 0,95 и k = 1.1. Для ряда параметров P, m значения k можно найтив [ ].

Случайные погрешности

Случайная погрешность - составляющая погрешности измерения, изменяющаяся случайным образом по знаку и значению в серии повторных измерений одной и той же физической величины, проведенных с одинаковой тщательностью в одних и тех же условиях. В появлении таких погрешностей нет никакой закономерности, они неизбежны, неустранимы и всегда присутствуют в результате измерения. Описание случайной погрешности возможно только на основе теории случайных процессов и математической статистики. В отличие от систематических, случайные погрешности нельзя исключить из результатов измерений за счет введения поправки, однако их можно существенно уменьшить путем увеличения числа наблюдений. На проведение измерений обычно оказывает влияние большое число случайных факторов, примерно одинаковых по величине, на малых по сравнению с общим воздействием. В этом случае в качестве математической модели для описания распределения результатов измерений правомерно применение нормального закона распределения.

Для нормального закона плотность вероятности равна

P(x) = exp[ - ],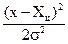

где 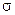- параметр рассеивания распределения, равный среднему квадратическому отклонению (СКО);

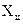- центр распределения, равный среднему арифметическому значению 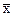или математическому ожиданию.

На практике применяется так называемое нормированное нормальное распределение. Оно получается при введении новой переменной

t = (x - )/ .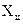

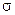Подставляя t в приведенную формулу плотности вероятности, получаем нормированное нормальное распределение, интегральная и дифференциальная функции которого соответственно равны:

F(t) = 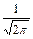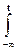e ^{- 0,5t} dt;p(t) = dF/dt = 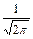e ^{- 0,5t} .

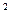Нормирование приводит к переводу начала координат в центр распределения и выражения абсциссы в долях среднеквадратического отклонения 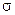. Значения этих функций можно найти в таблицах. Обычно там приводится значения определенного интеграла, называмого функцией Лапласа:

Ф(t) = 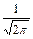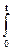e ^{- 0,5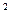t} dt.

Для нее справедливо: Ф(- 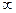) = -0,5; Ф(0) = 0; Ф(+ 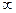) = 0,5; Ф(-t) = -Ф(t);

Функция F(t) связана с функцией Лапласа: F(t) =0,5+Ф(t).

В качестве значений результатов измерений принимают их статистические оценки.

Точечной оценкой результата измерений является среднее арифметическое значение измеряемой величины :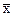

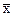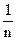
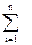= х_i.

Точечная оценка дисперсии

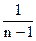
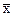D[x] = (x_i - )².

Среднеквадратическое отклонение случайной величины х определяется как корень квадратный из дисперсии. Оценка среднеквадратического отклонения 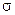случайной величины х обозначается S .

S = = .

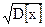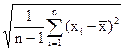Полученные оценки являются случайными величинами. При повторении серий из n измерений каждый раз будут получаться различные значения 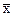и S . Они также являются случайными величинами, стремящимися к нормальному закону распределения при n → ∞.

Среднеквадратическая погрешность среднего арифметического S 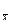является одной из основных характеристик точности измерений (см. подраздел 2.1).

Среднеквадратическая погрешность среднего квадратического отклонения S_s характеризует рассеяние среднего квадратического отклонения S измерений. Она используется значительно реже вышеуказанных, как и другие моменты распределений, и мы рассматривать ее не будем.

Грубые погрешности

Грубая погрешность (промах) - случайная погрешность, резко отличающаяся в данном ряду и в данных условиях от остальных результатов измерений. Как правило, она возникает от неправильных действий оператора, непредвиденных резких кратковременных изменений условий проведения измерений и т.д. Такие результаты обычно отбрасываются. Для обоснованного выделения их существуют критерии Райта, Романовского, Шарлье, Диксона и др. [1,2].

2.4.1. Критерии исключения грубых погрешностей.

Вопрос о том, содержит ли результат измерений грубую погрешность, решается общими методами проверки статистических гипотез. Проверяемая гипотеза состоит в том, что результат наблюдения х_i не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то в результатах измерений содержится грубая погрешность и этот результат исключают.

Для выявления грубых погрешностей задаются вероятностью q (уровнем значимости) того, что сомнительный результат действительно мог иметь место. Рассмотрим некоторые критерии исключения грубых погрешностей измерений.

Критерий “трех сигм”(критерий Райта) применяется для результатов измерений, распределенных по нормальному закону. По этому критерию результат с вероятностью q < 0,003 маловероятен и его можно считать промахом, если | 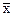- х_i| > 3S_x, где S_x оценка СКО измерений. Величины 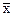, S_x вычисляются без учета экстремальных значений х_i.Данный критерий надежен при числе измерений n ³ 20...30.

Это правило считается слишком жестким, рекомендуется [1, 2] граница цензурирования в зависимости от объема выборки: при 6<n<100 она равна 4S_x; при 100<n<1000 − 4,5S_x; при 1000 <n <10000 − 5S_x.

В общем случае границы цензурирования t_гр 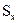выборки зависят от объема и распределения.

Критерий Романовского применяется, если число измерений n < 20. При этом вычисляется соотношение |( 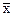- х_i)/S_x| = β и сравнивается с критерием β_Т, выбранным по таблице. Если β > β_Т, результат х_i считается промахом и отбрасывается.

Табл.1

Значения критерия Романовского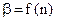

 

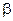
	n = 4	n = 6	n = 8	n = 10	n = 12	n = 15	n = 20
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,64	2,78
0,1	1,69	2,00	2,17	2,29	2,39	2,49	2,62

 

Применение данных критериев требует осмотрительности и учета объективных условий измерений. В сомнительных случаях лучше сделать дополнительные измерения (не взамен, а кроме них) и далее привлечь на помощь статистику.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: