Искажение изображения площади

Линейные смещения точек снимка, вызванные влиянием угла на­клона и рельефа местности, приводят к искажениям длин отрезков, и, следовательно, ограниченных ими площадей участков. Причем раз­дельные и независимые влияния угла наклона снимка и превышений между точками местности на искажение площа­дей суммируются.

\с р

Рис. 3.17. Искажение изображения площади

Влияние угла наклона на искажение площадей участков установим, исходя из сле­дующих соображений. Пусть имеем на плоской местности квадрат со стороной L, расположен­ный симметрично относительно главной верти­кали (рис. 3.17). На наклонном снимке этот

квадрат изобразится в виде трапеции со средней линией аЪ = 1\ и вы­сотой cd = /2- Площади участка на наклонном (Р) и на горизонталь­ном (Р°) снимках равны:

Р = l_xl₂ = (L/m_h) х (L/m_v) и Р° = J² = L²f²/H².

Искажение площади есть разность площадей Р и Р°, которая с уче­том масштаба по вертикали (3.29) и горизонтали (3.30) равна:

АР = р - р° =

^-l(cosa_c - ^sina_c) -1:

Более показательно относительное искажение площади:

(

\³
cosa_c-^sinaJ -1. (3.48)

Если центр участка k совпадает с главной точкой снимка (л:=0), то
^ = cos³a_c - 1. (3.49)

Расчеты по формуле (3.49) показывают, что площадь участка, изо­браженного на снимке симметрично относительно его главной точки, определяется с достаточно высокой точностью: при углах наклона а_с, равных 30 и 60 минут, относительное искажение составляет 1/ 8700 и 1/2900 соответственно. С такой же относительной ошибкой определя­ется сумма площадей отдельных участков снимка.

Влияние рельефа местности на искажение площадей участ­ков, изображенных на плановом снимке, найдем исходя из ошибок определения высоты фотографирования над средней плоскостью, рас­чет которой обычно выполняется по измеренным расстояниям между точками, опознанным на карте или на местности.

Площадь земельного участка на местности (Р) вычисляют по ре­зультатам ее измерения на снимке (Р):

Р° = Pm² = PxH²/f².

Неточное определение высоты фотографирования Н (или неучет превышений h между точками ее определения) приведет к ошибке оп­ределения масштаба и площади участка. Для установления ошибки функции Р° в зависимости от ошибки аргумента Н в соответствии с правилами теории ошибок измерений выполним дифференцирование:

F- f- н н

Примем dP° = АР и dH = h. Тогда относительная ошибка пло­щади

^ _{= 2}А. (3.50)

Р Н

Из полученной формулы следует, что влияние рельефа достаточно ощутимо: при высоте фотографирования Н = 2000 м и превышении Л=50 м относительная ошибка определения площади составит 5 % или 1/20 от ее величины, что существенно превышает допустимые ошибки определения площадей земельных участков при ведении землеустрои­тельных и кадастровых работ.

Физические источники ошибок аэроснимка

. Элементы реального изображения, полученного в процессе аэро­фотосъемки, содержат не только рассмотренные выше смещения и искажения, обусловленные особенностями центрального проектиро­вания, но и некоторые другие.

Особую группу составляют так называемые физические факторы, обусловленные влиянием атмосферной рефракции, кривизны Земли, дисторсии, деформации фотоматериала, его недостаточного выравни­вания в плоскость и пр.

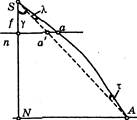
Влияние атмосферной рефракции связано с изменением температуры при уменьшении атмосферного давления, что приводит к изменению плотности воздуха, и, следовательно, показателя прелом­ления. В связи с этим световой луч, идущий от точки А к центру проек­ции S (рис. 3.18), будет претерпевать в каждом слое преломление. По­скольку с увеличением высоты съемки плотность слоев уменьшается, то луч будет постепенно удаляться от отвесной прямой, и его траектория окажется искривленной, причем вогнутость траектории всегда об­ращена к поверхности Земли. В конечном итоге это приведет к тому, что изображение точки местности А сместится из точки а в точку а'.

Угол между хордой SA и касательной к кривой SA в точке А на­зывают астрономической рефракцией (т), а между той же хордой и касательной в точке S - фотограмметрической рефракцией (к).

Отрезок аа! точки аэроснимка а, представляющий собой смеще­ние точки под влиянием рефракции, находится в отвесной плоскости

SNA (рис. 3.18), а его величина представляет собой изменение радиуса-вектора an = г при изменении угла у. Так как на плановом аэроснимке можно полагать, что г = / х tgy = = f х siny/cosy, то искомое искажение будет соответствовать дифференциалу этого выра­жения:

-dy.

Значение cos у найдем из прямоугольного треугольника Sna (рис. 3.18), из которого следует, что

Рас. 3.18. Смещения точек,

Вызнанные влиянием

Атмосферной рефракции

.COS" у + sin" у.

dr = /------ *— ----- ^Lrfy =

cos" у

/

cos" у

 

cos'

чя^ки-й-

С учетом этого и замены dy фотограмметрической рефракцией X поправка (ее знак противоположен знаку искажения) в положение точки аэроснимка, смещающая ее вдоль радиуса-вектора, будет равна:

dr

-ю

хХ.

(3.51)

Величина фотограмметрической рефракции X сравнительно не­велика и редко превышает 10", что при / = 150 мм, г_п = 100 мм соответствует искажению положения точки dr = Юмкм.

Исследованию способов определения фотограмметрической реф­ракции X посвящено немало работ. Широко известны, например, фор­мулы проф. Н. А. Урмаева, Ашенбреннера, Лейонхувуда, И. Ф. Куш-тина и др., полученные применительно к стандартной атмосфере.

Влияние кривизны Земли связано с тем, что земная поверхность не является плоско­стью, как это было принято при изучении зако­нов центрального проектирования и выводе формул связи координат точек снимка и местно­сти.

Рас. 3.19. Влияние кри­визны Земли

На рис. 3.19 показан плановый снимок Р, точка местности М и ее изображение т, отвес­ная линия SO и центр Земли О, принимаемой за шар радиуса R. Точка Mq является ортого­нальной проекцией точки М на предметную

плоскость Е, которой на снимке Р соответствует точка т°. Отрезок /тг/п⁰ и есть смещение 5^ точки т под влиянием кривизны Земли, причем геометрически 5^ эквивалентно смещению точки под влиянием рельефа местности, если в формуле (3.40) заменить h на ММ₀.

Для определения величины отрезка ММ о обратимся к рис. 3.19, из которого следует, что ММ₀ = ON - OK = R(\ - cosO), или

MM₀ = 2i?sin²9/2 * О,5Д0².

Значение угла 6 найдем из прямоугольного треугольника ОМК, причем, в виду его малости можно записать:

tg0«L/Л, откуда 6 «L/R * rm/R «(гЯ)/(/Д).

Тогда отрезок MMo=¹0,5R(rH)²/(fR)², а подстановка этого зна­чения в (3.40) вместо h дает

Нг^ъ

8k=T7±- (3.52)

____ п

Rf

Приняв II = 3 км, г = / = 100 мм и Д = 6370 км, найдем, что b_k = 0,023 мм.

Суммарное влияние кривизны Земли и атмосферной рефракции определяется как алгебраическая сумма соответствующих искажений. Знаки искажений всегда противоположны (рис. 3.18, 3.19), следова­тельно, влияние кривизны Земли частично компенсируется влиянием рефракции. Однако с увеличением высоты фотографирования влияние кривизны Земли становится все более ощутимым.

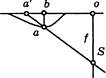
Ошибка выравнивания фотоматериала в плос­кость возникает в случае недостаточного прижима пленки к покров­ному стеклу прикладной рамки (§ 8) при экспонировании. Механизм влияния ошибки выравнивания показан на рис. 3.20, где а и а' - изо­бражения точки на поверхности эмульсионного слоя и в плоскости прикладной рамки соответственно; Ь - основание перпендикуляра, опущенного из точки а на плос­кость прикладной рамки. Обозначив оа' = г, аЬ = Д/ и а'Ъ = Лг, найдем:

Дг = -^-. (3.53)

Рис. 3.20. Ошибка

выравнивания фо- При г = f = 100 мм и Af = 10 мкм получим

томатсриала д_г = ₁₀ мкм.

Как видно, выравнивание фотопленки в плоскость должно выпол­няться с высокой точностыо, и ее учет осуществляется при обработке снимков на универсальных приборах и аналитическим способом.

Рис. 3.21. Точки определения дисторсии /

Влияние дисторсии объектива съемочной камеры проявля­ется в искривлении проектирующего луча и смещении точек изображения по радиальному направлению или перпендикулярно к нему (§ 6). Учет искажений в по­ложении произвольных точки снимка, вызванных влиянием дисторсии, выполняется либо по. полиному (1.9), либо путем интерполяция их значений по точ­кам определения дисторсии, размещенным по четы­рем (1-1, 2-2) или восьми (1-1, 2-2, 3-3, 4-4) централь­ным направлениям (рис. 3.21).

Деформация фотографического материала возни­кает при его фотохимической обработке и хранении материалов. Она проявляется в несовпадении расстояний между парами соответ­ственных точек, измеренных на исследуемом фотоматериале до (1о) и после (Z) его фотографической обработки. Показателем деформации является величина отношения ц = (I - 1о)/1о- Различают равномер­ную, неравномерную и случайную деформацию.

Равномерной называют деформацию, при которой \хх ⁼ Цу> ^т- е. изображение меняет свой масштаб по обеим координатным осям, так что величины углов не изменяются. Влияние равномерной деформа­ции полностью устраняется при фотограмметрической обработке с помощью конформных преобразований координат точек по формулам

х = а₀ + ах' - by' у = b₀+bx' + ay'

(3.54)

Параметры преобразования ао, &о> а и b определяют методом наименьших квадратов по результатам измерения координат точек, положение которых известно с высокой точностью.

Неравномерной называют деформацию, при которой \хх * Цу, т.е. возникают искажения точек изображения и величин углов между ни­ми. Для учета неравномерной деформации применяют полиномы вида

г' + azx'y'\

х = Oq + ОуХ + а₂у у = Ь₀+ Ь_гх' + Ь₂у

(3.55)

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: