Пример алгоритма для серии из двух опытов

Пусть имеется две серии эксперимента, в результате которых были получены две выборки объёмами n и m. Пусть нулевая гипотеза H₀: Генеральные средние обеих выборок совпадают. Чтобы проверить гипотезу H₀, необходимо:

1. Просуммировать элементы второй выборки (вычислить W)
2. Вычислить математическое ожидание случайной величины W. {\displaystyle M(W)=n(m+n+1)/2}
3. При справедливости H₀ математическое ожидание случайной величины W близко к статистике W.
4. Проверка гипотезы начинается с выбора уровня значимости — а
5. Вычислить пределы значимости (Из симметрии достаточно одного предела) и границу критической области W(a)
6. Справедливость неравенства W > W(a) свидетельствует о справедливости нулевой гипотезы. H₀ принимается на уровне значимости = а

 

Пример расчета T-критерия Вилкоксона

 

Допустим мы сравниваем между собой уровень тревожности подростков до и после тренинга уверенности в себе.

Шаг 1. Запишем значения в таблицу.

Шаг 2. Рассчитаем разность значений. Для данного случае типичным сдвигом будет считаться сдвиг в отрицательную сторону (7 значений, красный цвет заливки), а нетипичным в положительную сторону (3 значения, зеленый цвет заливки)

Шаг 3. Найдем значения шага 2 по модулю

Шаг 4. Проранжируем значения по модулю.

Все четыре шага приведены в таблице.

№	Уровень тревожности (до тренинга)	Уровень тревожности (после тренинга)	Шаг 2: Разность (после-до)	Шаг 3: Значение разности по модулю	Шаг 4: Ранг разности
			-1
			-3
			-1
			-3
			-5
			-3
			-1

Шаг 5. Найдем T эмпирическое вычислив сумму рангов в НЕтипичном направлении (зеленый цвет заливки).

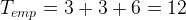
Шаг 6. Используя таблицу критических значений T-критерия Вилкоксона определяем T-критическое

6.1. Находим количество человек в выборке. n=10

6.2. Определяем T-критическое справа от значения количества человек в выборке. для p<0,05 T=10; для p<0,01 T=5

Шаг 7. Сравниваем T-критическо и T-эмпирическое.

Шаг 8 Делаем выводы.

 

Таблица критических значений T-критерия Вилкоксона

 

В таблице указаны критические значения T-критерия Вилкоксона в зависимости от уровня значимости.

N	p<0,05	p<0,01
		—
		—

 

 

В таблице критических значений T-критерия Вилкоксона находиться Т-критическое.

Если Е-критическое выше Т-эмпирического, то сдвиги в «типичную» сторону достоверное не преобладают.

 

T-критерий Вилкоксона предназначен для сравнения двух зависимых выборок между собой по уровню выраженности какого-либо признака.

С его помощью можно определить

1) направленность изменений,
2) выраженность изменений в зависимых выборках. С его помощью есть возможность определить в каком направлении сдвиг более интенсивен.

Параметрический аналог: t-критерий Стьюдента.

Непараметрический аналог: G-критерий знаков (менее мощный).

Суть применения T-критерия Вилкоксона сводится к тому, чтобы проранжировать разности значений в двух выборках.

Гипотезы

Н₀: Интенсивность сдвигов в типичном направлении не превосходит интенсивности сдвигов в нетипичном направлении.

H₁: Интенсивность сдвигов в типичном направлении превышает интен­сивность сдвигов в нетипичном направлении.

Особенности применения:

1. Признаки должны быть измерены в шкале порядка.
2. Эффективнее применять критерий, если разброс значений достаточно широк например от -30 до 30, если разброс значений не большой лучше применять G-критерий знаков (например от -3 до 3)
3. Минимальное количество замеров 5
4. Максимальное количество замеров 50 (ограничение обусловлено использованием таблицы критических значений T-Вилкоксона, при расчете в SPSS ограничение отсутствует)
5. Нулевые сдвиги не считаются замерами. Например группу могут составлять 50 человек, но у 10 из них сдвиги нулевые, следовательно мы будем рассчитывать значения исходя из 40 замеров)

 

Расчет T-критерия Вилкоксона заключается в выполнении следующих шагов:

1. Составить список значений испытуемых в первом и во втором замерах.
2. Найти разность по каждому замеру, т.е. вычесть из значений второго замера значения первого замера.
   Важно! Подсчитать количество отрицательных и количество положительных значений. Большее количество значений того или иного вида будет представлять из себя «типичный» сдвиг.
3. Найти значения разностей по модулю.
4. Ранжировать полученные на 4-ом шаге значения, по принципу меньшему значения приписывается меньший ранг. т.е. значение 1 — это 1 ранг.
5. Подсчитать T-эмпирическое, являющееся суммой рангов в НЕтипичном направлении: , где — ранговые значения сдвигов в НЕтипичном направлении
6. Определить T-критическое используя таблицу критических значений T-критерия Вилкоксона
   6.1. Определяем количество человек в выборке.
   6.2. Определяем T-критическое справа от значения количества человек в выборке в зависимости от уровня значимости.
7. Сравниваем T-эмпирическое и Т-критическое
8. Делаем вывод: Если — эмпирическое меньше T-критического, то сдвиг в «типичную» сторону преобладает на уровне значимости p<0,05

 

Пример

В выборке курсантов военного училища (юноши в возрасте от 18 до 20 лет) измерялась способность к удержанию физического волевого усилия на динамометре. Сначала у испытуемых измерялась максималь­ная мышечная сила каждой из рук, а на следующий день им предлага­лось выдерживать, на динамометре с подвижной стрелкой мышечное усилие, равное 1/2 максимальной мышечной силы данной руки. Почув­ствовав усталость, испытуемый должен был сообщить об этом экспери­ментатору, но не прекращать опыт, преодолевая усталость и неприят­ные ощущения - "бороться, пока воля не иссякнет". Опыт проводился дважды; вначале с обычной инструкцией, а затем, после того, как ис­пытуемый заполнял опросник самооценки волевых качеств по методике А.Ц. Пуни (Пуни А.Ц., 1977), ему предлагалось представить себе, что он уже добился идеала в развитии волевых качеств, и продемонст­рировать соответствующее идеалу волевое усилие. Подтвердилась ли гипотеза экспериментатора о том, что обращение к идеалу способствует возрастанию волевого усилия? Данные представлены в Табл. 3.5.

Таблица 3.5

Расчет критерия Т при сопоставлении замеров физического волевого усилия

Код имени испытуемого	Длительность удержания усилия на динамометре (с)	Разность (f после- f до)	Абсолютное значение разности	Ранговый номер разности
До измерения волевых качеств и обращения к идеалу (f до )	После измерения волевых качеств и обращения к идеалу (f после)
9 10 11	Г. Кос. Крив. Кур. Л. М. Р. С. Т. X. Ю.		63	- 39 - 27 + 3 - 19 - 38 - 8 + 4 - 4 - 38 + 25 - 18		9,5 2,5 2,5 9,5
Сумма

Для подсчета этого критерия нет необходимости упорядочивать ряды значений по нарастанию признака. Мы можем использовать ал­фавитный список испытуемых, как в данном случае.

Первый шаг в подсчете критерия Т - вычитание каждого инди­видуального значения "до" из значения "после"[1]. Мы видим из Табл. 3.5, что 8 полученных разностей - отрицательные и лишь 3 - положи­тельные. Это означает, что у 8 испытуемых длительность удержания мышечного усилия во втором замере уменьшилась, а у 3 - увеличилась. Мы столкнулись с тем случаем, когда уже сейчас мы не можем сфор­мулировать статистическую гипотезу, соответствующую первоначально­му предположению исследователя. Предполагалось, что обращение к идеалу будет увеличивать длительность мышечного усилия, а экспери­ментальные данные свидетельствуют, что лишь в 3 случаях из 11 этот показатель действительно увеличился. Мы можем сформулировать лишь гипотезу, предполагающую несущественность сдвига этого показателя в сторону снижения.

Сформулируем гипотезы.

Н₀: Интенсивность сдвигов в сторону уменьшения длительности мы­шечного усилия не превышает интенсивности сдвигов в сторону ее увеличения.

H₁: Интенсивность сдвигов в сторону уменьшения длительности мы­шечного усилия превышает интенсивность сдвигов в сторону ее увеличения.

На следующем шаге все сдвиги, независимо от их знака, должны быть проранжированы по выраженности. В Табл. 3.5 в четвертом слева столбце приведены абсолютные величины сдвигов, а в последнем столбце (справа) - ранги этих абсолютных величин. Меньшему значе­нию соответствует меньший ранг. При этом сумма рангов равна 66, что соответствует расчетной:

Теперь отметим те сдвиги, которые являются нетипичными, в данном случае - положительными. В Табл. 3.5 эти сдвиги и соответствующие им ранги выделены цветом. Сумма рангов этих "редких" сдвигов и составляет эмпирическое значение критерия Т:

где R_r - ранговые значения сдвигов с более редким знаком.

Итак, в данном случае,

Т_{эм n=} 1+2,5+7=10,5

По Таблице VI Приложения 1 определяем критические значения Т для n= 11:

Зона значимости в данном случае простирается влево. Действи­тельно, если бы "редких", в данном случае положительных, сдвигов не было совсем, то и сумма их рангов равнялась бы нулю. В данном же случае эмпирическое значение Т попадает в зону неопределенности:

Т_эмп < Т_кр (0,05)

Ответ: Н₀ отвергается. Интенсивность отрицательного сдвига показателя физического волевого усилия превышает интенсивность по­ложительного сдвига (р <0,05).

 

Таким образом, исследователю придется признать, что продолжительность удержания мышечного волевого усилия во втором замере снижается, и этот сдвиг неслучаен. Инструкция, ориентирующая испы­туемого на соответствие идеалу в развитии воли, оказалась гораздо ме­нее мощным фактором, чем какая-то иная сила - возможно, мышечное утомление, может быть, разочарование в себе или в возможностях дан­ного психологического эксперимента. А может быть, в момент второго замера просто перестает действовать какой-то мощный фактор, который был активен вначале? На все эти вопросы статистические методы не могут ответить, если в схему эксперимента не включена контрольная группа - в данном случае, выборка, уравновешенная с эксперименталь­ной группой по всем значимым характеристикам (полу, возрасту, про­фессии, месту обучения), у которой просто измерили бы вторично воле­вое усилие через такой же промежуток времени, не призывая соответ­ствовать идеалу в развитии воли.

Представим выполненные действия в виде алгоритма:

 

АЛГОРИТМ 9

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: