Подсчет критерия Q Розенбаума

1. Проверить, выполняются ли ограничения: n₁,n₂ ≥11, n₁ n₂≈n₂ Упорядочить значения отдельно в каждой выборке по степени воз­растания признака. Считать выборкой 1 ту выборку, значения в ко­торой предположительно выше, а выборкой 2 - ту, где значения предположительно ниже.

3. Определить самое высокое (максимальное) значение в выборке 2.

4. Подсчитать количество значений в выборке 1, которые выше макси­мального значения в выборке 2. Обозначить полученную величину как S₁.

5. Определить самое низкое (минимальное) значение в выборке 1.

6. Подсчитать количество значений в выборке 2, которые ниже мини­мального значения выборки 1. Обозначить полученную величину как S₂.

7. Подсчитать эмпирическое значение Q по формуле: Q=S₁+S2-

8. По Табл. I Приложения I определить критические значения Q для данных n₁ и n₂. Если Q_эмп равно Q_0,05 или превышает его, Н₀ от­вергается.

9. При n_1,n₂ >26сопоставить полученное эмпирическое значение с Q_{кp =} 8 (р≤ 0,05) и Q_{кp =} 10(p≤ 0,01). Если Q_эмп превышает или по крайней мере равняется Q_{кp =} 8, H₀ отвергается.

 

 

1. Критерий Фридмана (общая характеристика, ограничения, примеры использования).

Назначение критерия

Критерий χ² _r применяется для сопоставления показателей, изме­ренных в трех или более условиях на одной и той же выборке испы­туемых.

Критерий позволяет установить, что величины показателей от усло­вия кусловию изменяются, но при этом не указывает на направление изменений.

Описание критерия

Данный критерий является распространением критерия Т Вил­коксона на большее, чем 2, количество условий измерения. Однако здесь мы ранжируем не абсолютные величины сдвигов, а сами индиви­дуальные значения, полученные данным испытуемым в 1, 2, 3 и т. д. замерах.

Например, если у испытуемого в первом замере определена ско­рость прохождения графического лабиринта 54 сек, во втором замере -42 сек, а в третьем замере - 63 сек, то эти показатели получат ранги, соответственно, 2, 1, 3, поскольку меньшему значению, полученному во втором замере, мы начислим ранг 1, среднему значению, полученному в первом замере - ранг 2, а наибольшему значению, полученному в третьем замере - ранг 3.

После того, как все значения будут проранжированы, подсчитыва-ются суммы рангов по столбцам для каждого из произведенных замеров.

Если различия между значениями признака, полученными в раз­ных условиях, случайны, то суммы рангов по разным условиям будут приблизительно равны. Но если значения признака изменяются в раз­ных условиях каким-то закономерным образом, то в одних условиях будут преобладать высокие ранги, а в других - низкие. Суммы рангов будут достоверно различаться между собой. Эмпирическое значение критерия χ² _r и указывает на то, насколько различаются суммы рангов. Чем больше эмпирическое значение χ² _r, тем более существенные рас­хождения сумм рангов оно отражает.

Если χ² _rравняется критическому значению или превышает его, различия статистически Достоверны.

Гипотезы

Н₀: Между показателями, полученными (измеренными) в разных усло­виях, существуют лишь случайные различия.

H₁: Между показателями, полученными в разных условиях, существуют неслучайные различия.

Ограничения критерия

1. Нижний порог: не менее 2-х испытуемых (n ≥2), каждый из которых прошел не менее 3-х замеров (с≥3).

2. При с=3, n ≤ 9, уровень значимости полученного эмпирического зна­чения χ² _rопределяется по Таблице VII-A Приложения 1; при с=4, n ≤4, уровень значимости полученного эмпирического значения χ² _r определяется по Таблице VII-Б Приложения 1; при больших коли­чествах испытуемых или условий полученные эмпирические значения χ² _rсопоставляются с критическими значениями χ² _r, определяемыми по Таблице IX Приложения 1. Это объясняется тем, что χ² _rимеет распределение, сходное с распределением χ² _r. Число степеней свобо­ды v определяется по формуле:

v =c—1,

где с - количество условий измерения (замеров).

Пример

На Рис. 3.5. представлены графики изменения времени решения анаграмм в эксперименте по исследованию интеллектуальной настойчи­вости (Сидоренко Е. В., 1984). Анаграммы нужно было подобрать таким образом, чтобы постепенно подготовить испытуемого к самой трудной - а фактически неразрешимой - задаче. Иными словами, испы­туемый должен был постепенно привыкнуть к тому, что задачи стано­вятся все более и более трудными, и что над каждой последующей анаграммой ему приходится проводить больше времени. Достоверны ли различия во времени решения испытуемыми анаграмм?

Таблица 3.5

Показатели времени решения анаграмм (сек.)

Код имени испытуемого	Анаграмма 1: КРУА (РУКА)	Анаграмма 2: АЛСТЬ (СТАЛЬ)	Анаграмма 3: ИНААМШ (МАШИНА)
1. Л-в 2. П-о 3. К-в 4. Ю-ч 5. Р-о		235*[2]
Суммы
| Средние	10,2	248,8	9,4

Проранжируем значения, полученные по трем анаграммам каж­дым испытуемым. Например, испытуемый К-в меньше всего времени провел над анаграммой 1 - следовательно, она получает ранг 1. На вто­ром месте у него стоит анаграмма 3 - она получает ранг 2. Наконец, анаграмма 2 получает ранг 3, потому что она решалась им дольше двух других.

Сумма рангов по каждому испытуемому должна составлять 6.

Расчетная общая сумма рангов в критерии определяется по формуле:

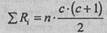
где n - количество испытуемых

с - количество условий измерения (замеров).

В данном случае,

Таблица 3.6

Показатели времени решения анаграмм 1, 2, 3 и их ранги (n= 5)

Код имени испытуемого	Анаграмма 1	Анаграмма 2	Анаграмма 3
	Время (сек)	Ранг	Время (сек)	Ранг	Время (сек)	Ранг
1. Л-в
2. П-о
3. К-в
4. Ю-ч
5. Р-о
Суммы

 

Общая сумма рангов составляет: 6+15+9—30, что совпадает с расчетной величиной.

Мы помним, что испытуемый Л-в провел 3 минуты и 55 сек над решением второй анаграммы, но так и не решил ее. Поскольку он ре­шал ее дольше остальных двух анаграмм, мы имеем право присвоить ей ранг 3. Ведь назначение трех первых анаграмм - подготовить испытуе­мого к тому, что над следующей анаграммой ему, возможно, придется думать еще дольше, в то время как сам факт нахождения правильного ответа не так существен.

Сформулируем гипотезы.

Н₀: Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, являются случайными.

H₁: Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, не являются случайными.

Теперь нам нужно определить эмпирическое значение χ² _rпо формуле:

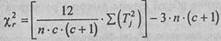
где с - количество условии;

п - количество испытуемых;

Т_i - суммы рангов по каждому из условий.

 

Определим χ² _rдля данного случая:

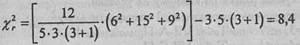
Поскольку в данном примере рассматриваются три задачи, то есть 3 условия, с=3. Количество испытуемых n= 5. Это позволяет нам воспользоваться специальной таблицей χ² _r, а именно Табл. VII-A При­ложения 1. Эмпирическое значение χ² _r=8,4 при с=3, n= 5 точно соот­ветствует уровню значимости р=0,0085.

Ответ: Но отклоняется. Принимается H₁. Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, неслучайны (р=0,0085).

Теперь мы можем сформулировать общий алгоритм действий по применению критерия χ² _r.

 

АЛГОРИТМ 10

Подсчет критерия χ² _rФридмана

1.Проранжировать индивидуальные значения первого испытуемого, полученные им в 1-м, 2-м, 3-м и т. д. замерах.

2.Проделать то же самое по отношению ко всем другим испытуемым.

3.Просуммировать ранги по условиям, в которых осуществлялись за­меры. Проверить совпадение общей суммы рангов с расчетной сум­мой.

4.Определить эмпирическое значение χ² _rпо формуле:

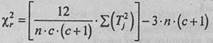
где с - количество условии;

п - количество испытуемых;

T_i - суммы рангов по каждому из условий.

5.Определить уровни статистической значимости для χ² _r

а)при с=3, n< 9 - по Табл. VII-A Приложения 1;

б)при с=4, n<4 - по Табл. VII-Б Приложения 1.

6.При большем количестве условий и/или испытуемых - определить количество степеней свободы v по формуле:

v =c-1,

где с - количество условий (замеров).

По Табл. IX Приложения 1 определить критические значения кри­терия χ² при данном числе степеней свободы V.

Если χ² _{r эмп} равен критическому значению χ² или превышает его, различия достоверны.

 

 

1. Критерий Манна-Уитни (общая характеристика, представление о ранжировании числовых данных, ограничения, примеры использования).

Назначение критерия

Критерий предназначен для оценки различий между двумя вы­борками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n₁•n₂≥ 3 или n₁=2, n₂≥5, и является более мощным, чем критерий Ро­зенбаума.

Описание критерия

Существует несколько способов использования критерия и не­сколько вариантов таблиц критических значений, соответствующих этим способам).

Этот метод определяет, достаточно ли мала зона перекрещиваю­щихся значений между двумя рядами. Мы помним, что 1-м рядом (выборкой, группой) мы называем тот ряд значений, в котором значе­ния, по предварительной оценке, выше, а 2-м рядом - тот, где они предположительно ниже.

Чем меньше область перекрещивающихся значений, тем более ве­роятно, что различия достоверны. Иногда эти различия называют раз­личиями в расположении двух выборок (Welkowitz J. et al., 1982).

Эмпирическое значение критерия U отражает то, насколько вели­ка зона совпадения между рядами. Поэтому чем меньше U_эмп, тем более вероятно, что различия достоверны.

Гипотезы

Н₀: Уровень признака в группе 2 не ниже уровня признака в группе 1.

H₁: Уровень признака в группе 2 ниже уровня признака в группе 1.

Ограничения критерия U

1. В каждой выборке должно быть не менее 3 наблюдений: n₁,n₂≥3; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.

2. В каждой выборке должно быть не более 60 наблюдений; n₁,n₂≤60. Однако уже при n₁,n₂>20 ранжирование становиться достаточно трудоемким.

На наш взгляд, в случае, если n₁,n₂>20, лучше использовать другой критерий, а именно угловое преобразование Фишера

Пример

Вернемся к результатам обследования студентов физического и психологического факультетов Ленинградского университета с помощью методики Д. Векслера для измерения вербального и невербального ин­теллекта. С помощью критерия Q Розенбаума мы в предыдущем па­раграфе смогли с высоким уровнем значимости определить, что уровень вербального интеллекта в выборке студентов физического факультета выше. Попытаемся установить теперь, воспроизводится ли этот резуль­тат при сопоставлении выборок по уровню невербального интеллекта. Данные приведены в Табл. 2.3.

Можно ли утверждать, что одна из выборок превосходит другую по уровню невербального интеллекта?

Таблица 2.3

Индивидуальные значения невербального интеллекта в выборках студентов физического (n₁=14 ) и психологического (n₂=12) факультетов

	Студенты-физики		Студенты-психологи
Код имени испытуемого	Показатель невербального интеллекта	Код имени испытуемого	Показатель невербального интеллекта
1.	И.А.		1.	Н.Т.
2.	К.А.		2.	О.В.
3.	К.Е.		3.	Е.В.
4.	П.А.		4.	Ф.О.
5.	С.А.		5.	И.Н.
6.	Ст.А.		6.	И.Ч.
7.	Т.А.		7.	И.В.
8.	Ф.А.		8.	К.О.
9.	Ч.И.		9.	P.P.
10.	ЦА.		10.	Р.И.
11.	См.А.		11.	O.K.
12.	К.Ан.		12.	Н.К.
13.	Б.Л.
14.	Ф.В.

Критерий U требует тщательности и внимания. Прежде всего, необходимо помнить правила ранжирования.

 

Правила ранжирования

1. Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1.

Наибольшему значению начисляется ранг, соответствующий количе­ству ранжируемых значений. Например, если n=7, то наибольшее значение получит ранг 7, за возможным исключением для тех слу­чаев, которые предусмотрены правилом 2.

2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.

Например, 3 наименьших значения равны 10 секундам. Если бы мы измеряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 сек; 10,5 сек; 10,7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получа­ет средний ранг:

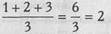
Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг:

3. Общая сумма рангов должна совпадать с расчетной, которая опре­деляется по формуле:

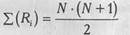
где N - общее количество ранжируемых наблюдений (значений). Несовпадение реальной и расчетной сумм рангов будет свидетельст­вовать об ошибке, допущенной при начислении рангов или их сум­мировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.

При подсчете критерия U легче всего сразу приучить себя дейст­вовать по строгому алгоритму.

АЛГОРИТМ 4

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: