АЛГОРИТМ 5 Подсчет критерия Н Крускала-Уоллиса

1. Перенести все показатели испытуемых на индивидуальные карточки.

2. Пометить карточки испытуемых группы 1 определенным цветом, например красным, карточки испытуемых группы 2 - синим, карточки испытуемых групп 3 и 4 - соответственно, зеленым и желтым цветом и т. д. (Можно использо­вать, естественно, и любые другие обозначения.)

3. Разложить все карточки в единый ряд по степени нарастания признака, не считаясь с тем, к какой группе относятся карточки, как если бы мы работали с одной объединенной выборкой.

4. Проранжировать значения на карточках, приписывая меньшему значению меньший ранг. Надписать на каждой карточке ее ранг. Общее количество рангов будет равняться количеству испытуемых в объединенной выборке.

5. Вновь разложить карточки по группам, ориентируясь на цветные или другие принятые обозначения.

6. Подсчитать суммы рангов отдельно по каждой группе. Проверить совпадение общей суммы рангов с расчетной.

7. Подсчитать значение критерия Н по формуле:

где N - общее количество испытуемых в объединенной выборке;

n - количество испытуемых в каждой группе;

Т - суммы рангов по каждой группе.

8а. При количестве групп с=3, n₁•n₂•n₃ ≤5определить критические значения и со­ответствующий им уровень значимости по Табл. IV Приложения 1.

Если Н_эмп равен или превышает критическое значение H_0,05, H₀ отвергается.

8б. При количестве групп с>3 или количестве испытуемых n₁•n₂•n₃>5, определить критические значения χ² по Табл. IX Приложения 1.

Если Н_эмп равен или превышает критическое значение χ², H₀ отвергается.

 

Воспользуемся этим алгоритмом при решении задачи о неразре­шимых анаграммах. Результаты работы по 1-6 шагам алгоритма пред­ставлены в Табл. 2.6.

Таблица 2.6

Подсчет ранговых сумм по группам испытуемых, работавших над четырьмя неразрешимыми анаграммами

Группа 1: анаграмма ФОЛИТОЫ (n1 =4)	Группа 2: анаграмма КАМУСТО (n2 =8)	Группа 3: анаграмма СНЕРАКО (n3=6)	Группа 4: анаграмма ГРУТОСИЛ (n4=4)
Длительность	Ранг	Длительность	Ранг	Длительность	Ранг	Длительность	Ранг
	3.5		3.5
Суммы		38,5		82,5
Средние		9,6		10,3		11,3		16,0

Общая сумма рангов =38,5+82,5+68+64=253. Расчетная сумма рангов:

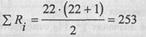
Равенство реальной и расчетной сумм соблюдено.

Поскольку таблицы критических значений критерия Н преду­смотрены только для количества групп с = 3, а в данном случае у нас 4 группы, придется сопоставлять полученное эмпирическое значение Н с критическими значениями у}. Для этого вначале определим количест­во степеней свободы V для c=4:

v=c- 1 = 4 - 1 = 3

Теперь определим критические значения по Табл. IX Приложе­ния 1 для v =3:

Ответ: Н₀ принимается: 4 группы испытуемых, получившие разные неразрешимые анаграммы, не различаются по длительности по­пыток их решения.

Критерий тенденций Пейджа (общая характеристика, ограничения, примеры использования).

L - критерий тенденций Пейджа

Описание критерия L дается с использованием руководства J.Greene, M. D'Olivera (1989).

Назначение L - критерия тенденций

Критерий L Пейджа применяется для сопоставления показателей, измеренных в трех и более условиях на одной и той же выборке испы­туемых.

Критерий позволяет выявить тенденции в изменении величин признака при переходе от условия к условию. Его можно рассматривать как продолжение теста Фридмана, поскольку он не только констатирует различия, но и указывает на направление изменений.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: