Основы методологии расчета

ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН

 

Статистический показатель представляет собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности.

Статистический показатель это не просто число, как в математике. Любой статистический показатель должен иметь три обязательных атрибута: количественную определенность, место и время. (Каждый статистический показатель так же, как и название статистической таблицы или рисунка должен отвечать на три вопроса: что? где? когда?) Кроме того все статистические показатели числа именованные, т.е. имеют единицы измерения.

Статистическая информация, как правило, представлена с помощью обобщающих показателей.

Обобщающий статистический показатель отражает количественную сторону изучаемой совокупности общественных явлений, представляет собой их величину, выраженную соответствующей единицей измерения.

Все многообразие статистических показателей может быть представлено с помощью абсолютных, относительных и средних величин.

Абсолютные величины, выражающие размеры (уровни, объемы) явлений и процессов, получают непосредственно в результате статистического наблюдения и сводки исходной информации.

По способу выражения размеров изучаемых явлений абсолютные величины подразделяются на индивидуальные и суммарные, которые представляют собой один из видов обобщающих величин.

Индивидуальные — характеризуют размеры количественных признаков у отдельных единиц.

Абсолютные величины — всегда числа именованные, имеющие определенную размерность, единицы измерения. В зависимости от различных причин и целей анализа применяются натуральные, денежные (стоимостные) и трудовые единицы измерения.

Относительные показатели (ОП) - это обобщающие показатели, которые характеризуют количественное соотношение двух сопоставляемых статистических показателей. При расчете относительных величин в числителе всегда находится показатель, отражающий то явление, которое изучается, т.е. сравниваемый показатель, а в знаменателе — показатель, с которым производится сравнение, принимаемый за основание или базу сравнения.

 

Относительные величины в зависимости от того, за сколько единиц принята база сравнения могут принимать разную форму выражения.

Основание (база сравнения) может быть приравнено к 1, 100, 1000, 10000 единиц. В соответствии с этим относительные показатели выражаются в форме:

– коэффициентов (доля единицы или число раз),

– процентов (%),

– промилле (‰),

– продецимилле.

Выбор формы выражения относительного величины, к которой следует обратиться в каждом конкретном случае, зависит от характера данных и результатов, которые получаются при сопоставлении величин. Следует выбирать такую форму относительного показателя, которая с большей ясностью и наглядностью выразит данное соотношение.

Если непосредственно при делении получается число 2 и более, то результат следует так и оставить (в целых числах, в крайнем случае, с одним знаком после запятой). Форма выражения – коэффициент, единица измерения - разы.

Когда сравниваемые величины различаются незначительно, то полученное при делении число следует представить в форме процентов. Процентную форму получают, если основание принять за 100, то есть значение коэффициента необходимо умножить на 100.

К относительным показателям в форме промилле и продецимилле обращаются для того, чтобы придать относительной величине удобный для восприятия вид, освободив их от большого числа знаков после запятой в десятичных дробях. Эти формы относительных показателей чаще используются в демографической статистике. Промилльные соотношения получают, если базу сравнения принять за 1000, то есть значение коэффициента необходимо умножить на 1000.

По познавательной роли и направлению сопоставления различают следующие виды относительных величин:

- структуры,

- координации,

- интенсивности,

- сравнения,

- динамики,

- плана, планового задания, прогноза,

- отношения фактических величин к плановым (нормативным, оптимальным, максимально возможным).

Относительные величины структуры (d_i) характеризуют состав совокупности, а также распределение признаков или единиц по группам и показывают, какую долю в общем итоге составляет каждая часть совокупности.

или .

Как правило, относительные показатели структуры выражаются в процентах. Сумма долей равна 1,00 или 100 %.

. .

Пример

Численность населения города 347 тыс. чел, в том числе мужчины – 164 тыс. чел, женщины – 183 тыс. чел.

Тогда структура населения по полу будет выглядеть следующим образом:

Доля мужчин:

Доля женщин::

Сопоставляя относительные величины структуры во времени, выявляют структурные сдвиги (. Сопоставляя относительные величины структуры (доли, удельные веса) в пространстве, выявляют структурные различия (). Как те, так и другие измеряются в процентных пунктах.

Пример

Доля женщин на 6 пунктов превышает долю мужчин

пунктов.

Структурные сдвиги показывают, на сколько процентных пунктов увеличилась (или уменьшилась) i-тая доля показателя в одном периоде по сравнению с другим.

Структурные различия показывают, на сколько процентных пунктов i-тая доля показателя объекта А больше (или меньше) доли этого же показателя объекта В.

Чтобы наглядно показать структурные сдвиги (различия), используют секторную, круговую, столбиковую (высота столбца равна 100 %), стоклеточную диаграммы.

Относительные величины координации характеризуют соотношение двух частей одной совокупности и показывают, сколько единиц (или человек, или рублей) одной части совокупности приходится на 1 или на 10 или на 1000 единиц (или человек, или рублей) другой части этой же совокупности. В качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. Относительные величины координации выражаются в виде кратных отношений. Записывают 9: 10.

Пример

На начало года численность специалистов с высшим образованием, занятых в ассоциации «А», составила 153 человека, а численность специалистов со средним специальным образованием — 106 человек. Рассчитаем относительную величину координации:

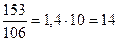
т.е. на 10 специалистов со средним специальным образованием приходится 14 специалистов с высшим образованием.

Относительные величины интенсивности характеризуют соотношение разноименных связанных между собой величин. Они содержат двойные единицы измерения - числителя и знаменателя.

Когда числитель и знаменатель дроби имеют одинаковые единицы измерения, то относительные величины интенсивности чаще выражаются в процентах.

Пример

Число предприятий розничной торговли региона на конец года составило 6324 единиц. Численность населения данного региона на ту же дату составила 234,2 тыс. чел.

предприятия розничной торговли на каждую тысячу жителей, более корректно: 2,7∙10=27, следовательно, на каждые 10000 человек в данном регионе приходится 27 предприятий розничной торговли

Относительные величины сравнения - это отношение одноименных показателей, относящихся к разным объектам или территориям за один и тот же период или на один и тот же момент времени.

В числителе рекомендуется ставить показатель изучаемого объекта.

Пример

Прибыль предприятия А по итогам работы за год сложилась в размере 586 млн руб., а прибыль предприятия Б – 378 млн руб.

Сравним на сколько процентов финансовый результат предприятия А превышает финансовый результат предприятия Б.

или 1,55∙100 – 100 = 55 %, следовательно, прибыль предприятия А превысила прибыль предприятия Б на 55 %.

Сравним на сколько процентов финансовый результат предприятия Б меньше финансового результата предприятия А.

или 0,65∙100 – 100 = - 35 %, следовательно, прибыль предприятия Б меньше прибыли предприятия А на 35 %.

Относительные величины динамики применяют для характеристики изменения явления во времени. Они исчисляются делением величины показателя на данный момент (или за данный период) времени на величину показателя на другой момент (или за другой, более ранний, период) времени, принятый за базу. Относительные величины динамики выражаются в форме коэффициентов или процентов. Коэффициент динамики показывает, во сколько раз уровень одного периода больше уровня другого периода или какую часть в долях единицы составляет данный уровень от уровня принятого за базу сравнения. Темп динамики (Т) показывает, сколько процентов показатель текущего периода составляет по отношению к показателю базисного периода. Темп динамики может быть меньше или больше 100 %.

Если темп динамики больше 100 %, правильнее назвать его темпом роста.

Относительными показателями динамики считаются также темпыизменения (), которые называются или темпами прироста (+), или темпами снижения (-).

Пример

В отчетном году выручка от продажи продукции составила 948 млн руб., в прошлом – 773 млн руб. Требуется определить на сколько процентов изменилась выручка от продажи.

Следовательно, выручка в отчетном году по сравнению с прошлым годом выросла 22,6 %.

Все субъекты финансово-хозяйственной сферы, начиная от небольших семейных предприятий и заканчивая крупнейшими корпорациями, осуществляют перспективное планирование своей деятельности, а также сравнивают реально достигнутые результаты с ранее намеченными. Для этой цели используют относительные величины плана, планового задания, прогноза и относительные величины реализации плана.

Относительные величины плана, планового задания, прогноза (ОВп)исчисляются по формуле:

Относительная величина реализации плана (ОВ рп) рассчитывается как отношение уровня, фактически достигнутого в текущем периоде (У факт или ), к запланированному на этот период же уровню данного показателя (У план):

Наиболее распространенными видами относительных величин являются показатели структуры, динамики и координации.

Решение типовой задачи

Таблица 3- Возрастной состав населения России

Миллион человек

Социально-демографическая группа населения	1995 г.	2002 г.
Моложе трудоспособного возраста	33,2	26,8
В трудоспособном возрасте	84,2	87,3
Старше трудоспособного возраста	30,2	29,9

Определите:

1) Возрастную структуру населения в 1995 и 2002 гг.

2) Сдвиги в возрастной структуре населения.

3) Темпы изменения численности каждой возрастной группы за 7 лет.

 

 

Условие и результаты решения подобных задач следует представлять в табличной форме.

Таблица 4 - Состав и структура населения России

Социально-демографическая группа населения	1995 г.	2002 г.	Сдвиги в структуре, пункты	Темп изменения, %
млн чел.	% к итогу	млн чел.	% к итогу
Моложе трудоспособного возраста	33,2	22,5	26,8	18,6	-3,9	-19,3
В трудоспособном возрасте	84,2	57,0	87,3	60,6	3,6	3,7
Старше трудоспособного возраста	30,2	20,5	29,9	20,8	0,3	-1,0
Всего	147,6	100,0	144, 0	100,0	-	-2,4

 

Пояснения к таблице

Исходные данные выделены курсивом.

1) Для расчета структуры явления предварительно следует определить итог изучаемой совокупности, как сумму значений показателей по всем составляющим данного явления (147,6 млн чел. – численность населения РФ в 1995 г., и 144 млн чел. – в 2002 г).

- расчет доли (d_i) каждой группы в общем объеме совокупности осуществляется по формуле:

.

Например, доля лиц в возрасте младше трудоспособного определяется как отношение числа лиц данной возрастной группы к общей численности населения:

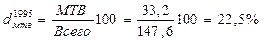, следовательно, доля лиц младше трудоспособного возраста в 1995 году составляла 22,5 %.

 

2) Для расчета структурных сдвигов (структурных изменений), необходимо определить структуру совокупности за два периода и вычислить разность долей соответствующих групп.

- расчет структурных сдвигов выполняется по формуле:

=18,6 - 22,5= - 3,9 пункта, следовательно, доля лиц младше трудоспособного возраста за 7 лет уменьшилась на 3,9 пункта.

3)Темп изменения характеризует, на сколько процентов изменилось значение показателя за рассматриваемый промежуток времени.

- расчет темпа изменения осуществляется по формуле:

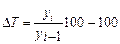
, следовательно, численность населения в возрасте младше трудоспособного снизилась на 19,3 %.

Расчеты по другим строкам таблицы выполняются аналогично.

7. СРЕДНИЕ ВЕЛИЧИНЫ: ВИДЫ И МЕТОДИКА РАСЧЕТА

Средняя величина (СВ) - это обобщающий показатель, в котором находят выражение действие общих условий, закономерности изучаемого явления.

Статистические средние рассчитываются на основе массовых данных правильно статистически организованного массового наблюдения (сплошного и выборочного). Однако статистическая средняя будет объективна и типична, если она рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений).

Расчет различных средних величин производится по соответствующим математическим формулам, которые дает математическая статистика. Задача общей теории статистики - дать смысловую, преимущественно экономическую, интерпретацию математических формул.

Признак, по которому рассчитывается средняя, называют осредняемым (возраст, доход, прибыль, рентабельность, число детей и т.д.). Значения признака у отдельных единиц или группы единиц называются вариантами и обозначаются х_1, х₂ , х₃ … и т.д.

Определить среднюю можно через ее логическую формулу, через исходное соотношение средней (ИСС):

 

 

В статистике применяют различные виды средних: арифметическую, гармоническую, геометрическую, квадратическую, хронологическую и структурные средние - моду и медиану.

Средние (кроме моды и медианы) исчисляются в двух формах: простой и взвешенной.

Наиболее часто используемые средние:

- средняя арифметическая,

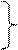- средняя гармоническая,

- средняя геометрическая, Как правило, применяются при обработке

- средняя хронологическая. рядов динамики

 

Каждый вид средней имеет свои особые свойства, которые наиболее полно соответствуют решению поставленной задачи. Поэтому одним из основных вопросов, который возникает при определении средних, является выбор способа расчета, т.е. выбор вида и формы средней.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: