 |
Выбор вида и формы средней
|
|
|
|
Выбирая тот или иной вид средней (арифметическую или гармоническую), следует исходить из экономической сущности осредняемого признака, то есть признака, по которому исчисляется средняя, и наличия исходных данных.
Выбору вида средней должен предшествовать анализ взаимосвязи имеющихся в распоряжении данных.
Средняя арифметическая
Средняя арифметическая - наиболее часто используемый вид средней. Средняя арифметическая может быть простой (невзвешенной) и взвешенной.
Средняя арифметическая простая равна сумме значений признака, деленной на их число:
 ,
,
где х - варианта (значение признака),
n - число единиц (объем) признака.
Простая средняя арифметическая применяется в том случае, когда все варианты признака встречаются по одному разу или имеют одинаковый вес в совокупности.
Пример
Выручка от продажи товаров (товарооборот) магазинов одной торговой за сети за месяц характеризуется следующими данными, млн руб.:
35,4 44,2 29,7 33,8 41,9 37,1 39,3
Требуется определить средний размер выручки от продажи (товарооборота), приходящийся на одну торговую точку (один магазин).
Конкретно для данного примера ИСС будет определяться следующим образом:
осредняемый признак (х) – выручка от продажи (ВП), следовательно,

Так как объем изучаемой совокупности небольшой и исходные данные не сгруппированы, то для расчета используем формулу средней арифметической простой:
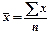 ,
,
 =
=  млн руб.
млн руб.
Средний размер выручки от продажи, приходящийся на одну торговую точку составил 37,3 млн руб.
Средняя арифметическая взвешенная применяется в том случае, когда варианты встречаются различное число раз или имеют различный вес в данной совокупности. При ее исчислении отдельные значения признака х (варианты) умножаются (взвешиваются) на частоту  , c которой каждое значение признака повторяется в данной совокупности.
, c которой каждое значение признака повторяется в данной совокупности.
|
|
|

Среднюю арифметическую взвешенную приходится применять также при вычислении общей средней для всей совокупности из частных групповых средних.
Надо иметь в виду, что если в качестве весов выступают абсолютные величины (f), то всякие промежуточные действия при расчете средней величины должны давать экономически значимые показатели.
Пример
Таблица 5 - Распределение частных домохозяйств по размеру в РФ
| Размер домашнего хозяйства, чел. | х | 5 и более | ||||
| Количество домашних хозяйств, тысяч | f |
Определите средний размер домашнего хозяйства.
Конкретно для данного примера ИСС будет определяться следующим образом:
осредняемый признак (х) – размер домашнего хозяйства (Рдх),
частоты (f) – количество домашних хозяйств, следовательно,

Так как объем изучаемой совокупности большой, а размах вариации значений признака мал и признак является дискретным, то данные наблюдения обработаны и представлены в виде дискретного ряда распределения.
Для расчета среднего значения признака в дискретном ряду распределения используют среднюю арифметическую взвешенную:

 =
=  чел.
чел.
Средний размер домашнего хозяйства в Российской Федерации составляет 2,6 чел.
В ряде случаев, частоты ряда распределения (f) могут быть представлены не абсолютными величинами, а относительными величинами структуры (d), которые показывают, какую долю составляет та или иная группа в общем объеме совокупности. В таких случаях формула средней арифметической взвешенной будет модифицирована (преобразована) и выглядеть следующим образом:
 ,
,
где х – значения осредняемого признака
d – доля группы, выраженная в виде коэффициента (долях единицы) 
|
|
|
Рассмотрим вариант расчета средней арифметической взвешенной по данной формуле, используя информацию предыдущего примера.
Пример
Таблица 6 - Распределение частных домохозяйств по размеру в РФ
| Размер домашнего хозяйства, чел. | х | 5 и более | Всего | |||||
| Количество домашних хозяйств | тысяч | f | ||||||
| % к итогу | d | 22,3 | 27,5 | 23,8 | 17,0 | 9,4 | 100,0 |
Доля домашних хозяйств, состоящих из 1 человека определяется:

Аналогично рассчитывается доля и других групп домашних хозяйств, результаты расчетов представлены в таблице 6.
Теперь, используя данные о возможных размерах домашних хозяйств (х) и структуру совокупности (d), рассчитает средний размер домашних хозяйств. В данном случае в качестве весов будет выступать доля (d) каждой группы совокупности.
Расчет осуществляется по модифицированной формуле средней арифметической взвешенной:
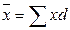
 =2,6 чел.
=2,6 чел.
Средний размер домашнего хозяйства в Российской Федерации составляет 2,6 чел.
Как видно, результаты расчетов, выполненные по обычной и модифицированной формулам средней арифметической взвешенной совпадают.
ВНИМАНИЕ! При использовании данной формулы в расчет подставляют долю, выраженную в виде коэффициента. Если в расчет подставляют долю, выраженную в виде процентов, то полученный результат необходимо поделить на 100.
Результаты группировки могут быть представлены в виде интервальных рядов распределения, в этом случае изучаемый признак будет представлен не конкретным, а интервальными значениями. Расчет среднего значения признака в данном случае осуществляется также по обычной или модифицированной формулам средней арифметической взвешенной. Но предварительно интервальный ряд следует представить в дискретной форме, определив середину каждого интервала.
Середина интервала (х') определяется как средняя арифметическая простая между верхней (Хв) и нижней (Хн) границами соответствующего интервала.
х'= 
Формулы для расчета средней арифметической взвешенной в интервальном ряду выглядят следующим образом:

или
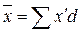
Пример
Таблица 7 - Распределение численности занятых в экономике Архангельской области по возрастным группам
| Возрастная группа, лет | Процент к итогу | |
| До 20 | 2,8 | |
| 20-24 | 10,9 | |
| 25-29 | 13,3 | |
| 30-49 | 53,2 | |
| 50-54 | 12,0 | |
| 55-59 | 5,3 | |
| 60-72 | 2,5 | |
| Все население | 100,0 |
Определите средний возраст занятого населения.
|
|
|
Информация в таблице 7 представляет собой интервальный ряд распределения. Группировочный непрерывный признак (х) – возраст, представлен с помощью интервалов значений, а частоты выражены в виде структуры совокупности (d) и характеризуют долю каждой возрастной группы в общей численности занятого населения Архангельской области.
В данном случае для определения среднего возраста необходимо воспользоваться модифицированной формулой средней арифметической взвешенной и предварительно следует определить середины интервалов.
Первый интервал «До 20» является открытым, так как имеет только одну верхнюю границу, для определения его нижней границы необходимо воспользоваться правилом: «Величина открытого интервала условно приравнивается к величине смежного с ним интервала». Смежный интервал 20-24 года, его величина (h) определяется как разность между верхней и нижней границами:
h=Хв ─ Хн=24─20=4 года,
следовательно, в соответствии с правилом величина первого интервала также будет равняться 4 годам. Условно границы первого интервала составят 16-20 лет.
Для наглядности расчет середины каждого интервала представлен в таблице 8.
Таблица 8 – Расчет середины интервала
| Возрастная группа, лет | Процент к итогу | Расчет | Середина интервала, лет |
| х | d,% | 
| х' |
| До 20 | 2,8 | 
| |
| 20-24 | 10,9 | 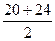
| |
| 25-29 | 13,3 | 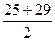
| |
| 30-49 | 53,2 | 
| 39,5 |
| 50-54 | 12,0 | 
| |
| 55-59 | 5,3 | 
| |
| 60-72 | 2,5 | 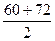
|
Несколько условно преобразовав интервальный ряд в дискретный, рассчитаем средний возраст занятых по формуле:

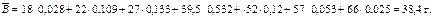
Средний возраст занятого населения в Архангельской области составил 38 лет.
|
|
|


