Расчет предварительно напряженной плиты покрытия типа 2 – Т размером 3 x 12 м

Данные для проектирования

 

Бетон класса В35 с расчетными характеристиками при коэффициенте условий работы γ_{b 2}= 0,9: R_b = 0,9 · 19,5 = 17,55 МПа; R_bt= 0,9 · 1,3 =1,17 МПа; R_b,ser = 25,5 МПа; R_bt,ser = 1,95 МПа; Е_b = 3,1 · 10⁴ МПа. Передаточная прочность бетона R_bp = 0,8 · В = 0,8 · 35 = 28 МПа; расчетные характеристи­ки бетона для класса, численно равного передаточной прочности (В ≡ R_bp = 28 МПа): R 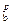=16 МПа; R 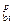=1,14МПа; R 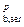= 20,6МПа; R 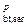= 1,72 МПа; E 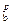=28,2 · 10³ МПа.

Напрягаемая арматура - канаты Ø9 К7 из высокопрочной проволоки Ø3 Вр-II (R_s = 1145 МПа; E_s = 1,8 · 10⁵ МПа).

Арматура каркасов и сеток - проволока класса Вр-I (при Ø4 мм: R_s = 365 МПа; R_sw = 265 МПа; при Ø5: R_S= 360 МПа; R_sw = 260 МПа; E_s = 1,7 · 10⁵ МПа).

Натяжение арматуры - механическое на упоры форм. Изделие под­вергается пропарке при атмосферном давлении. К трещиностоикости плиты предъявляются требования 3-й категории.

Размеры поперечного сечения плиты показаны на рис. 5.8.

Нагрузки на плиту

 

Нагрузка от веса плиты при γ_f = 1 и γ_п = 0,95:

на 1 м² -

на 1 м погонный плиты - 1,614 · 3 = 4,842 кН/м,

где G = A · l · γ = 0,2078 · 12 · 2,5 = 6,234 т - масса панели;

А = 2,98 · 0,03 + (0,4 - 0,03) · 0,5 · (0,16 + 0,08) · 2 + 0,04 · 0,37 · 0,5 · 4 = 0,2078 м² - площадь поперечного сечения плиты;

В = 3 м - ширина плиты; l = 12 м - длина плиты;

γ = 2,5 т/м³ - плотность бетона.

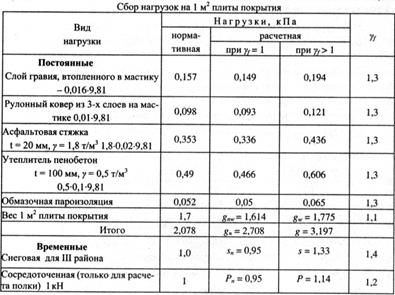
Сбор нагрузок на плиту приведен в табл. 3.2. Для расчета полки плиты учтена сосредоточенная нагрузка Р_п = 1кН (вес рабочего с инструментом). Ве­личины расчетных нагрузок приведены с учетом коэффициента надежности γ_п = 0,95.

 

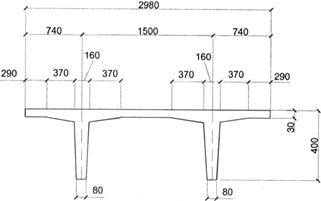
Рис. 5.8. Поперечное сечение плиты 2-Т

 

Таблица 5. 2

Расчет полки плиты

Для расчета полки вырезаем полосу шириной 1 м перпендикулярно продольным ребрам и рассматриваем ее как однопролетную двухконсольную балку с расчетным пролетом l ₀ = 1500 мм и консолями а = 740 мм (рис. 5.9).

 

 

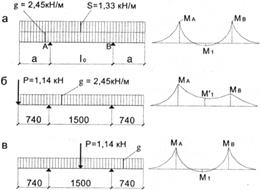
Рис. 5.9. К расчету полки плиты

 

♦ Определение нагрузок на полку плиты. Переменную толщину полки заменим эквивалентной постоянной из условия равенства площадей.

Площадь сечения продольных ребер

A ₁ = 2 · [0,16 · 0,07 + 0,5 · (0,16 + 0,08) · (0,4 - 0,07)] = 0,1016 м².

Площадь полки плиты

A'_f=A – А ₁ = 0,2078 - 0,1016 = 0,1062 м².

Эквивалентная толщина полки:

Постоянная нагрузка от веса 1 м² полки при γ_f = 1,1 и γ_n = 0,95

g_f = 0,04 · 2,5 · 9,81 · 1,1 · 0,95 = 1,025 кН/м².

Полная постоянная нагрузка на полку (вес кровли и полки)

g = 1,422 + 1,025 = 2,45 кН/м².

♦ Определение усилий в полке плиты. Расчетные усилия определяем для трех схем загружения полки (см. рис. 5.9).

1. При действии постоянной и снеговой нагрузок (схема а):
М_А=М_В = -(g + s) · a² / 2 = -(2,45 + 1,33) · 0,74²/ 2 = -1,035 кНм;
М ₁ =М ₀ - M_A = (g+ s) · l ₀ ² / 8 - M_A = (2,45 + 1,33) · 1,5² / 8 - 1,035 = 0,028 кНм;

Q_a,l = -(g + s) · a = -(2,45 + l,33) · 0,74 ≈ -2,8 кН;

Q _{a ,r} = (g + s)(0,5l₀ + a)- Q_A,l = (2,45 + 1,33) · (0,5 · 1,5 + 0,74) - 2,8 = 2,83 кН.

Момент по грани опоры при b = 160 мм

М = М_А + Q_A,l · b / 2 = -1,054 + 2,85 · 0,16 / 2 = -0,811 кНм.

2. Действие постоянной и сосредоточенной нагрузки (схема б):
М_А = -(g · a² / 2 + Р · а) = -(2,45 · 0,74² / 2 + 1,14 · 0,74) = -1,514 кНм;
М_B = -ga² / 2 = -2,45 · 0,74² / 2 = -0,671 кНм;

M ′₁= g · l ₀² / 8 - (М_А + М_В) / 2 = 2,45 · 1,5² / 8 - (1,514 + 0,671) / 2 = -0,403 кНм;

Q_a,l = -(g · a + P) = -(2,45 · 0,74 + 1,14) = -2,953 кН;

R_a = g · (l ₀ + 2 · a) / 2 + Р · (а + l₀) / l₀ = 2,45 · (1,5 + 2 · 0,74) /2 + 1, · (0,74+ 1,5) / / 1,5 = 5,353кН;

Q _{a ,r} = R_a - Q_a,l = 5,353 - 2,953 = 2,4 кН.

Наибольший изгибающий момент по грани опоры А

М=М_А + Q _a,r · b / 2 = -1,514 + 2,4 · 0,16 / 2 = -1,322 кНм.

3. При действии постоянной и кратковременной сосредоточенной на­
грузок в середине пролета (схема в):

М_А=М_B = -g · a² / 2 = -2,45 · 0,74² / 2 = -0,671 кНм;

М ₁ = gl ₀² / 8 + Рl ₀ / 4 - М_A = 2,45 · 1,5² / 8+ 1,14 · 1,5 / 4 - 0,671 = 0,446 кНм;

Q_a,l = -g · a = -2,45 · 0,74 = -1,813 кН;

R_A = 8 · (l ₀ + 2 · a) / 2 + 0,5 · F = 2,45 · (l,5 + 2 · 0,74) / 2 + 0,5 · 1,14 = 4,221 кН;

Q _a,r = R_A - Q_a,l = 4,221 - 1,813 = 2,408 кН.

Наибольший изгибающий момент по грани опоры

М = М_А + Q_a,l · b /2 = -0,671 + 1,813 · 0,16 / 2 = -0,526 кНм.

Расчетные значения изгибающих моментов в сечениях полки:

- по грани опоры М= -1,322 кНм;

- в середине пролета М ₁= 0,446 кНм; М′ ₁ = -0,403 кНм.

Отрицательный момент в начале утолщения полки (на расстоянии 300 мм от оси плиты) при загружении по схеме б определим приближенно, в предположении линейного изменения момента

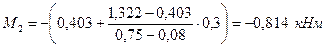
♦ Подбор арматуры полки. Армирование полки выполняем сварной сеткой из проволоки Ø5 Вр - I. Площадь рабочей арматуры на 1 м ширины полки в сечении по грани опоры при М_A = -1,322 кНм:

h ₀ = 70 – 10 - 5 = 55 мм;

ξ = 0,025;

A_s = ξ · R_b · b · h₀ / R_s = 0,025 · 17,55 · 1000 · 55 / 365 ≈ 67мм².

To же в сечении на расстоянии 300 мм от оси плиты:

h ₀ = 30 -10 - 5 = 15 мм;

ξ = 0,233;

A_s = 0,233 · 17,55 · 1000 · 15 / 360= 170,4 мм².

Принимаем сварную рулонную сетку с поперечной рабочей армату­рой Ø 5 Вр-I с шагом 100 мм (A_s = 196 мм² / м) и продольной Ø4 Вр-I с шагом 300 мм.

 

Расчет продольных ребер

♦ Нагрузки и усилия. Расчетная схема продольного ребра дана на рис.5.10. Расчетный пролет ребра по осям при длине площадки опирания плиты l_sup = 120 мм

l ₀= l - l_sup = 11,96 – 2 · 0,12 / 2 = 11,84 м.

Нагрузка на 1 погонный м плиты при ее ширине b_п = 3 м:

при γ_f= 1: постоянная - g_n = g_n · b_n = 2,708 · 3 = 8,12 кН/м; в т.ч. собственный вес g_nw = g_nw · b_n = 1,614 · 3 = 4,84 кН/м;

продолжительно действующая

q_nl = (g_n + 0,3s_n)b_n = (2,708+0,3 · 0,95) · 3 = 8,98кН/м;

полная - q_n = (g_n + s_n)b_n = (2,708 + 0,95) · 3 = 10,97 кН/м;

при γ_f > 1: полная q = (g + s)b_n = (3,197 + 1,33) · 3 = 13,58 кН/м.

Усилия в продольных ребрах:

при γ_f = 1: от всей нагрузки Mn = q_n · l ₀²/8 = 10,97 · 11,84² / 8 = 192,2 кНм;

в т.ч. от продолжительно действующей

M_l = q_nll ₀² / 8 = 8,98 · 11,84² / 8 = 157,4 кНм;

при γ_f > 1: M = q · l ₀ ² /8 = 13,58 · 11,84² / 8 = 238 кНм;

Q = q · l ₀ / 2 = 13,58 · 11,84 / 2 = 80,4 кН.

 

 

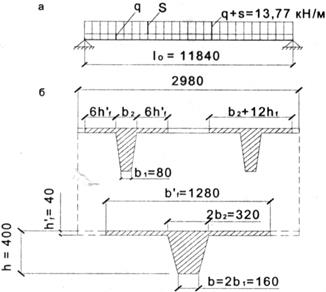
Рис. 5.10. К расчету продольных ребер: а - расчетная схема; б - приведение поперечного сечения плиты к расчетному тавровому сечению

 

♦ Подбор продольной арматуры ребер. Поперечное сечение плиты заменяем эквивалентным тавровым (рис. 5.10, б). При отсутствии поперечных ребер и отношении h′_f / h = 40 / 400 = 0,1 расчетная ширина полки тавра со­ставит

b′_f = 2 · (b₂ + h′_f) = 2(160 + 12 · 40) = 1280 мм;

средняя ширина ребра тавра b = b ₁+ b ₂ = 80 + 160 = 240 мм; расстояние от центра тяжести растянутой арматуры до нижней грани предварительно принимаем а = 50 мм.

1. h ₀= h - а = 400 - 50 = 350 мм.

2.

где ω = 0,85 - 0,008 · R_b = 0,85 - 0,008 · 17,55 = 0,71;

σ_sR = R_s + 400 - σ_sp - ∆σ_sp = R_s + 400 - 0,6 · R_s = 1145 + 400 -0,6 · 1145 = 858 МПа; σ_sp / R_s = 0,6 [4, табл.26, прим.1];

∆σ_sp = 0[4, п. 3.6]; σ_sc,u = 500 МПа при γ_{b 2} < 1.

Устанавливаем положение нижней границы сжатой зоны

R_bb′_fh′_f · (h ₀ - 0,5h′_f) = 17,55 · 1280 · 40 · (350 - 0,5 · 40) = 296 · 10⁶ Нмм = 296 кНм > М = 238кНм,

нижняя граница сжатой зоны проходит в полке (x < h′_f), поэтому арматуру подбираем как для прямоугольного сечения.

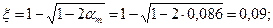
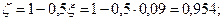
x = ξ · h ₀= 0,09 · 350 = 31,5 мм < h′_f = 40 мм - нейтральная ось дей­ствительно проходит в полке.

Коэффициент γ_{s 6} = η - (η - 1) · (2 · ξ / ξ_R - 1) = 1,15 - (1,15 - 1) · (2 · 0,09/0,441-1) = = 1,24 > η = 1,15; принимаем γ_{s 6} = η = 1,15. Площадь сечения продольной напрягаемой арматуры

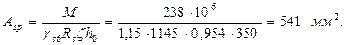
Принимаем 12 Ø9 К7 (A_sp = 611 мм) и располагаем по 6 Ø9 К7 в каждом ребре.

Для обеспечения трещиностойкости зоны, наиболее удаленной от линии действия усилия предварительного обжатия, принимаем также верхнюю напрягаемую арматуру в количестве 15% от площади рабочей предварительно напряженной арматуры A_sp, т. е. A′_sp = 0, 15 · A_sp = 0,15 · 611 = = 92 мм²

В каждом ребре принимаем по одному канату Ø9 К7 (A′_sp =51 · 2 = 102 > 92мм), которые располагаем в верхней зоне ребра вблизи полки.

Нижние и верхние продольные стержни каркасов принимаем из обыкновенной проволоки Ø5 Bp-l (A_S = A′_S= 39 мм ).

Коэффициент армирования ребер плиты:

♦ Определение геометрических характеристик приведенного се­чения плиты. В растянутой зоне сечения находятся 12 Ø9 К7 (A_sp = 611 мм²) и 2 Ø5 Bp-I (A_s = 39,3 мм² - нижние стержни каркасов); в сжатой зоне - 2 Ø9 К7 (A_sp = 102 мм²), 2 Ø5 Bp-I (A_s = 39,3 мм² - верхние стержни каркасов) и 11 Ø4 Bp-I (A_s - 138,6 мм² - продольные стержни сетки полки).

 

 

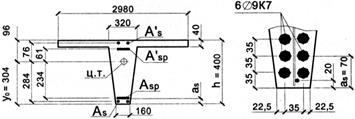
Рис. 5.11. К определению геометрических характеристик приведенного сечения плиты

 

Площадь приведенного сечения

A_red = A + αA_sp + αA′_sp + αA_s + αA′_s = 2980 · 40 + 160 - 360 + 2 · 80 · 360 / 2 + 5,8 · 611 + 5,8 · 102 + 5,48 · (39,3 + 39,3 + 138,6) = 210926 мм²,

где а =1,8 · 10⁵ / 3,1 · 10⁴= 5,8 для арматуры К7;

а =1,7 · 10⁵ /3,1 · 10⁴ = 5,48 для арматуры Вр-1.

Статический момент приведенного сечения относительно нижней грани

S_red = 2980 · 40 · (400 – 40 / 2) + 160 · 360 · 180 + 80 · 360(2 / 3) · 360 + 5,8 · · 611 · 70 + 5,8 · 102 · (400 - 35) + 5,48 · 39,3 · 20 + 5,48 · 39,3 · (400 - 20) + 5,48 · 138,6 · (400 - 15 – 4 / 2) = 63,4 · 10⁶ мм³.

Расстояние от центра тяжести приведенного сечения:

до нижней грани y ₀ = S_red / A_red = 63,4 · 10⁶ / 210926 ≈ 301 мм;

до верхней грани h – y ₀ = 400 - 301 = 99 мм.

Момент инерции приведенного сечения относительно оси, проходя­щей через центр тяжести:

I_red = 2980 · 40³ / 12 + 2980 · 40 · (99 - 20)² + 160 · 360³ / 12 + 160 · 360 · (301 - 180)² + 2 · 80 · 360³ / 36 + 80 · 360 · (301 - 2/3 · 360)² + 5,8 · 611 · (301 - 70)² + 5,8 · · 102 · (99 - 35)² + 5,48 · 39,3 · (301 - 20)² + 5,48 · 39,3 · (99 - 20)² + 5,48 · 138,6 · (99 - 17)² = 27,5 · 10⁸ мм⁴.

Момент сопротивления относительно нижней грани:

W_red = I_red / y ₀ = 27,510⁸ / 301 = 9,14 · 10⁶ мм³.

То же с учетом неупругих деформаций сжатого бетона

W_pl = γW_red= 1,75 · 9,14 · 10⁶ ≈ 16 · 10⁶ мм³.

Момент сопротивления относительно верхней грани

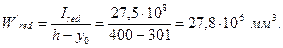
То же с учетом неупругих деформаций бетона

W′_pl =γ'W'_red = 1,5 · 27,8 · 10⁶ = 41,7 · 10⁶мм³.

Расстояния от центра тяжести сечения до ядровых точек:

до верхней r_t= W_red / A_red = 9,14 · 10⁶ / 210926 ≈ 43 мм;

до нижней r_b = W'_red / A_red = 27,8 · 10⁶ / 210926 ≈ 132мм. Расстояния от центра тяжести приведенного сечения до центра тяже­сти арматуры:

- напрягаемой в растянутой зоне y_sp = 301 - 70 = 231 мм;

- напрягаемой в сжатой зоне y'_sp = 99 - 35 = 64мм;

- ненапрягаемой в растянутой зоне y_s = 301 - 20 = 281 мм;

- ненапрягаемой в сжатой зоне y_s' = 99 - 20 = 79мм.

♦ Определение потерь предварительного напряжения. Для обес­печения требуемой трещиностойкости плиты предварительное напряжение арматуры принимаем максимально допустимым по п. 1.15 [4]: (σ_sp= 0,95 R_s,ser = 0,95 · 1370 МПа ≈ 1300 МПа; для верхней напрягаемой арма­туры σ'_sp = σ _sp = 1300 МПа.

Первые потери

1. От релаксации напряжений в арматуре

σ ₁= σ' ₁ = (0,22 · σ_sp / R_s,ser - 0,1) · σ_sp = (0,22 · 1300 / 1370 - 0,1) · 1300 = 141,4 МПа.

2.Потери от температурного перепада отсутствуют (σ ₂ = 0), так как нагрев арматуры и формы происходит одновременно.

3.От деформации анкеров при инвентарных зажимах

σ ₃= σ' ₃= (1,25 + 0,l5 · d) · E_s / l = (1,25 + 0,15 · 9) · 1,8 · 10⁵ / 12100 = 38,7 МПа,

где l = 12100 мм - длина натягиваемых канатов.

4.От деформации стальной формы σ ₅ = σ' ₅ = 30 МПа.

5.От быстронатекающей ползучести бетона:

- усилие обжатия Р ₀с учетом вычисленных потерь

Р ₀= (σ_sp - σ ₁ - σ ₃ - σ ₅ ) · А_sp + (σ'_sp - σ' ₁ - σ' ₃ - σ' ₅) · A'_sp = (1300 - 141,4 - 38,7 - 30) · · 611 + (1300 - 141,4 - 38,7 - 30) · 102 = 777098 H = 777 кН;

- эксцентриситет усилия Р₀ относительно центра тяжести приведен­ного сечения

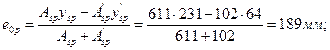
- сжимающие напряжения в бетоне на уровне центра тяжести арма­туры A_sp (y = y_sp = = 231 мм) с учетом разгружающего действия изгибающего момента от веса плиты M_w = γ_f g_nwl ₀² / 8 = 0,9 · 4,84 · 11,84² / 8 = 76,4 кНм:

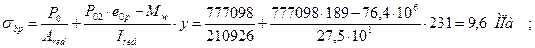
- то же на уровне центра тяжести арматуры A'_sp

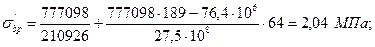
σ_bp / R_bp = 9,6 / 28 = 0,343 < α = 0,8;

σ ₆ = 34 · σ_bp / R_bp = 34 · 0,343 = 11,7 МПа;

σ' ₆ = 34 · σ'_bp / R_bp = 34 · 2,04 / 28 = 2,48 МПа,

где α = 0,25 + 0,025 · R_bp = 0,25 + 0,025 · 28 = 0,95 > 0,8; принимаем α = 0,8 [4, п. 1.25, табл. 5, поз. 6].

Итого первые потери:

σ_{l 1} = σ ₁ + σ ₃ + σ ₅+ σ ₆= 141,4 + 38,7 + 30 + 11,7 = 221,8 МПа;

σ'_{l 1} = σ' ₁ + σ' ₃ + σ' ₅+ σ' ₆= 141,4 + 38,7 + 30 + 2,48 = 212,6 МПа.

Вторые потери

6.От усадки класса бетона В 35: σ ₈= σ' ₈= 35 МПа.

7.От ползучести бетона:

- напряжения в напрягаемой арматуре с учетом первых потерь σ_{sp 1} = σ_sp - σ_{l 1} = 1300 - - 221,8 = 1078,2 МПа;

σ'_{sp 1} = σ'_sp - σ'_{l 1} = 1300 - 212,6 = 1084,4 МПа;

- то же в ненапрягаемой арматуре

σ_s = σ ₆ = 11,7 МПа; σ'_s = σ' ₆ = 2,48 МПа;

- усилие обжатия с учетом первых потерь

P ₁ = σ_{sp 1} · A_sp + σ'_{sp 1} · A'_sp - σ _s · A_s - σ'_s · A'_s = 1078,2 · 611 + 1087,4 · 102 -11,7 · 39,3 - 2,48 · (39,3 + 138,6) = 768794 H ≈ 769 кН;

- эксцентриситет приложения усилия P ₁

е _{о p 1} = (σ_{sp 1} · A_sp · y_sp + σ'_s · A'_s · y'_s - σ'_{sp 1} · A'_sp · y'_sp - σ_s · A_s · y_s)/ P ₁ = (1078,2 · 611 · 231 + 2,48 · 178 · 79 - 1087,4 · 102 · 64 - 11,7 · 39,3 · 281) / 769 · 10³= 189мм.

Проверим сжимающие напряжения в бетоне на уровне крайнего во­локна (у₀ = 301 мм) в стадии предварительного обжатия (без учета разгру­жающего действия собственного веса плиты):

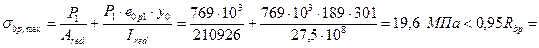
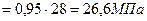- требование п. 1.22 [4] выполняется;

- напряжение в бетоне на уровне центра тяжести арматуры A_sp с
учетом разгружающего действия веса плиты

- тоже на уровне центра тяжести арматуры A'_sp

- при σ_bp / R_bp = 9,4 / 28 = 0,336 < 0,75 потери от ползучести

σ ₉ = 128 · σ_bp / R_bp = 128 · 0,336 ≈ 43 МПа;

σ' ₉ = 128 · σ'_bp / R_bp = 128 · 2,04 / 28 = 9,3 МПа.

Итого вторые потери: σ _{l 2} = 35 + 43 = 78 МПа;

σ '_{l 2}= 35 + 9,3 = 44,3 МПа.

Полные потери предварительного напряжения:

σ_l = σ_{l 1} + σ_{l 2} = 221,8 + 78 ≈ 300 МПа > 100 МПа;

σ'_l = σ'_{l 1} + σ'_{l 2} = 212,6 + 44,3 ≈ 257 МПа > 100 МПа.

Предварительные напряжения с учетом всех потерь:

в арматуре A_sp σ_{sp 2} = σ_sp - σ_l = 1300 - 300 = 1000 МПа;

в арматуре A'_sp σ'_sp2 = σ'_sp - σ'_l = 1300 - 257 = 1043МПа;

в арматуре A_s σ'_s = σ' ₆ + σ' ₈ + σ' ₉ = 2,48 + 35 + 9,3 ≈ 47МПа;

в арматуре A'_s σ_s = σ ₆ + σ ₈ + σ ₉ = 11,7 + 35 + 43 ≈ 90МПа.

Усилие обжатия с учетом всех потерь при коэффициенте γ_sp =1

P₂ = σ_{sp 2} A_sp + σ'_{sp 2} A'_sp - σ_sA_s - σ'_sA'_s = 1000 · 611 + 1043 · 102 - 90 · 39,3 - 47 · (39,3 + 138,6) = 705488 H = 705кН.

Эксцентриситет усилия Р ₂относительно центра тяжести приведен­ного сечения

♦ Проверка прочности нормальных сечений. Проверку выполним для стадии изготовления и для стадии эксплуатации.

Стадия изготовления

Проверка прочности производится как для внецентренно сжатого элемента, при этом усилие в напрягаемой арматуре определяется с учетом первых потерь при γ_sp > 1 и вводится в расчет как внешняя продольная сила

N_P = [ γ_sp · (σ_sp - σ_{l 1} ) - 330] · А_sp = [1,1 · (1300- 221,8) – 330] · 611 = 523 · 10³ Н = 523кН, приложенная с эксцентриситетом е _{0 р 1}.

Прочность плиты проверяем в местах расположения монтажных пе­тель (на расстоянии l ₁ = 0,8 м от торцов), где отрицательные моменты от веса плиты суммируются с моментами от действия усилия предварительно­го обжатия (см. рис. 5.12).

Изгибающий момент в этом сечении от веса плиты с учетом коэффициента динамичности k_d= 1,4

M_w = γ_f · k_d · g_nw · l ₁ ² / 2= 1,1 · 1,4 · 4,84 · 0,8² / 2 ≈ 2,4 кНм.

В наиболее обжатой нижней зоне плиты расположена напрягаемая арматура площадью A'_sp = 611 мм (12 Ø9 К7); ненапрягаемую арматуру 2 Ø5 Вр-I в этой же зоне в расчете не учитываем, так как она не удовлетворяет конструктивным требованиям, касающихся сжатой арматуры.

 

Рис. 5.12. К расчету плиты в стадии обжатия

 

В верхней менее обжатой (растянутой) зоне в этой стадии работают продольные стержни сетки полки (11 Ø4 Вр-I) общей площадью A_s= 138,6 мм, напрягаемая арматура 2 Ø9 К7 с площадью A_sp = 102 мм и продольные стержни каркасов 2 Ø5 Вр-I с площадью A_s = 39,3 мм (рис. 5.13, сеч. 1-1 и узел В). Расстояние от центра тяжести всей этой арматуры до верхней грани плиты а ≈ 25 мм, рабочая высота сечения h' ₀ = 400 - 25 = 375 мм.

Расчетный эксцентриситет усилия N_p относительно центра тяжести растянутой (верхней) арматуры

e = h' ₀ - а' + М_w / N_p = 375-70 + 2,4 · 10⁶ / 523 · 10³ = 310мм.

Расчетное сопротивление бетона сжатию, соответствующее передаточной прочности R_bp ≡ В = 28 МПа с учетом коэффициента γ_{b 8}= 1,1 [4, табл. 14, п. 56]: R 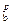= 1,1 · 16 = 17,6 МПа.

Граничную относительную высоту сжатой зоны бетона принимаем по табл. 33 [4]: ξ_R = 0,51. Так как ширина ребра плиты переменна, в первом при­ближении примем ее для уровня x ≈ 170 мм, т.е.

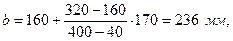
тогда высота сжатой зоны бетона

что полностью совпадает с первоначально принятым значением.

При ξ = х / h ₀ = 170 / 375 = 0,453 < ξ_R = 0,51 несущую способность проверяем из условия

N_p · e ≤ M_u = R 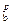bx(h' ₀- 0,5 · х) + R_sc · A'_s(h' ₀- a'); (5.11)

N_p · e = 523 · 10³ · 310 = 162 · 10⁶ Нмм =162 кНм;

М_и = 17,6 · 236 · 170 · (375 - 0,5 · 170) + 0 ≈ 205 · 10⁶ Нмм = 205 кНм.

Тогда N_p · e = 162 кНм < М_и = 205кНм, т.е. прочность плиты в стадии изго­товления обеспечена.

Стадия эксплуатации

Рабочая высота сечения h ₀ = 400 - 70 = 330 мм (см. рис. 5.11).

Коэффициент точности натяжения арматуры

γ_sp = 1 ± ∆ γ_sp

где ∆ γ_sp = 0.1 при механическом способе натяжения, тогда

γ_sp = 1 - 0,1 = 0,9 и γ'_sp= 1 + 0,1 = 1,1.

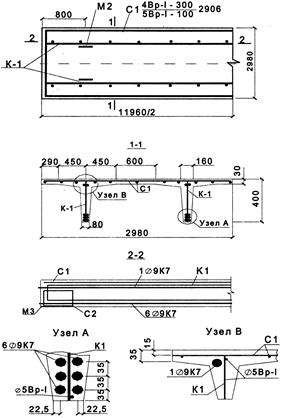
Рис. 5.13. Армирование плиты 2-Т

 

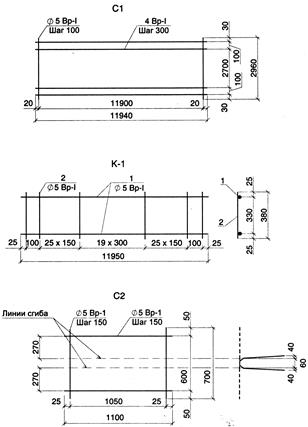
Рис. 5.14. Арматурные изделия плиты 2-Т

 

Граничная относительная высота сжатой зоны бетона

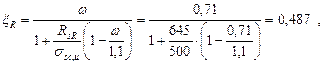
где σ_sR = R_s + 400 - γ_spσ_sp2 - ∆ σ_sp2 = 1145 + 400 - 0,9 · 1000 - 0 = 645 МПа. Здесь ∆ σ_{sp 2}= 0 Для арматуры класса К7 [4, п. 3.6].

Положение нейтральной оси определим из условия

R_s · A_sp + R_s · A_s ≤ R_b · b'_f · h'_f + R_sc · A'_s + σ_sc · A_sp , (5.12)

где σ_sc = σ_sc,u - γ'_sp · σ'_{sp 2} = 500 - 1,1 ·1043 = -647 МПа - напряжение, с кото­рым вводится в расчет прочности напрягаемая арматура A'_sp.

Проверяем условие (5.12)

1145 · 611 + 360 · 39,3 = 713743 Н = 713 кН < 17,55 · 1280 · 40 - 647 · 102 = 832566 Н = 832 кН - нейтральная ось проходит в полке (x < h'_f).

При проверке условия (5.12) не учтена сжатая арматура A'_s, так как она не удовлетворяет конструктивным требованиям п. 5.39 [4].

Относительная высота сжатой зоны бетона при γ_{s 6} = 1

Так как ξ = 0,105 <ξ_R = 0,487, сжатая арматура не требуется.

Коэффициент γ_{s 6}для высокопрочной арматуры

γ_{s 6}= η - (η - 1) · (2 ξ / ξ_R - 1) = 1,15 - (1,15 - 1) · (2 · 0,105 / 0,487 - 1) = 1,24 > η = 1,15, поэтому принимаем γ_{s 6} = η = 1,15.

Относительная высота сжатой зоны бетона при γ_{s 6} = 1,15

α_m = ξ · (1 - 0,5 ξ) = 0,119 · (1 - 0,5 · 0,119) = 0,112.

Предельный момент, воспринимаемый сечением:

М_и = α_m · R_b · h'_f · h ₀ ² + R_sc · A'_s (h ₀ - a'_s) + σ_sc · A'_sp (h₀ - a'_p) = 0,112 · 17,55 · 1280 · 330² + 0 - 647 · 102 · (330 - 35) = 254,5 · 10⁶ Нмм = 254,5 кНм > М = 238 кНм - следовательно, несущая способность нор­мальных сечений плиты обеспечена.

♦ Расчет прочности наклонных сечений. Проверяем прочность наклонных сечений на действие поперечных сил. Максимальная попереч­ная сила на опоре Q_max = 80,4 кН. Расчетная ширина сечения ребра b = 2 · (b ₁ + b ₂ ) / 2 = 2 · (80 +160) / 2 = 240 мм.

Выясняем необходимость постановки расчетной поперечной армату­ры:

1. Коэффициент φ_f учитывающий влияние сжатых свесов:

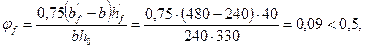
где

2. Усилие обжатия P ₂ с коэффициентом γ_sp = 0,9

P ₂ = 0,9 · 1000 · 611 + 0,9 · 1043 · 102 - 89 · 39,3 - 47 · 178 ≈ 634 кН.

3. Коэффициент, учитывающий влияние продольных сил:

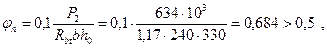
принимаем φ_п = 0,5 [4, п. 3.22].

4. k = 1 + φ_п + φ_f = 1 + 0,5 + 0,09 = 1,59 > 1,5,
принимаем k = 1,5 [4, п. 3.22].

5. q ₁ = q= 13,58 кН/м - временная нагрузка сплошная [4, п.3.22].

6. При q ₁= 13,58 кН/м < 0,16 · φ_{b 4} (1 + φ_п)R_bt · b = 0,16 · l,5 ·(1 + 0,5) · 1,17 · 240 = 101 кН/м длину с проекции наклонного сечения при­нимаем равной c_max = 2,5 h ₀= 2,5 · 330 = 825 мм.

7. Поперечное усилие, воспринимаемое бетоном без развития наклон­
ных трещин:

Q_b,u = 1,5 · (1 + φ_п) · R_bt · b · h ₀ ² / с = 1,5 · (1 + 0,5) · 1,17 · 240 · 330² / 825 = 83398 Н = 83 кН.

8. Так как Q_b,u = 83 кН > Q_max = 80,4 кН, то поперечная арматура по
расчету не нужна. Принимаем поперечную арматуру конструктивно из Ø4
Вр-I с шагом 150 мм на приопорных участках длиной l / 4 = 11,98 / 4 ≈ 3,0 м и
шагом 300 мм на остальной части пролета.

В нашем случае наклонные трещины не развиваются, поэтому про­верку прочности наклонной полосы между наклонными трещинами можно не выполнять. Проверим необходимость расчета прочности наклонных се­чений на действие изгибающего момента, поскольку напрягаемая арматура не имеет анкеров на концах. Такой расчет можно не производить, если из­гибающий момент М в нормальном сечении, проходящем через конец зоны передачи напряжений (рис. 5.15, сеч. 1-1), меньше момента образования нормальных трещин, вычисленного с заменой R_bt,ser на R_bt.

 

 

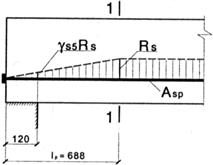
Рис. 5.15. К расчету прочности наклонных сечений продольных ребер плиты на дей­ствие изгибающего момента

 

Длина зоны анкеровки (иначе длина зоны передачи напряжений с арма­туры на бетон) для предварительно напряженной арматуры по п. 2.26 [4]

где значения φ_р , σ_sp, ∆λ_p приняты по п. 2.26 и табл. 24 [4].

Начало зоны анкеровки принимаем у торца плиты, тогда изгибаю­щий момент в конце зоны анкеровки:

М_х = Q · x - q · x² / 2 = 80,4 · 0,628 - 13,58 · 0,628² / 2 = 47,8кНм,

где х = l_p - l_sup / 2 = 688 - 120 / 2 = 628 мм = 0,628 м - расстояние от середи­ны площадки опирания плиты до конца зоны анкеровки.

Для определения момента М_сrс предварительно вычисляем следую­щие необходимые параметры:

напряжение в сжатом волокне бетона

 

 

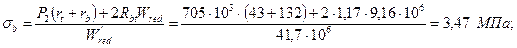
коэффициент, учитывающий неупругие деформации сжатого бетона:

φ = 1,6 - σ_b / R_b = 1,6 - 3,47 / 17,7 = 1,4 > 1, принимаем φ = 1; расстояние от центра тяжести приведенного сечения до верхней (наиболее удаленной от рассматриваемого волокна) ядровой точки с учетом коэффициента φ

r =φW_red / A_red= 1 · 9,16 · l0⁶ / 210926 ≈ 43мм;

момент усилия обжатия Р ₂относительно верхней ядровой точки

M_rp = P ₂ · (e _{0 p 2} + r) = 705 · 10³ · (190 + 43) = 164 · 10⁶ Нмм = 164кНм.

Момент трещинообразования для нормального сечения, проходяще­го через конец зоны анкеровки напрягаемой арматуры:

M_crc = R_bt · W_pl + M_rp= 1,17 · 16 · 10⁶ + 164 · 10⁶ ≈ 183 · 10⁶ Н-мм = 183 кНм.

Так как момент трещинообразования М_сrс = 183 кНм превышает из­гибающий момент от внешних нагрузок М_х = 47,5 кНм, проверку прочно­сти наклонного сечения на действие изгибающего момента можно не про­изводить.

 

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: