Расчет поля оболочки на изгиб между диафрагмами

 

Расчет сводится к определению изгибающей нагрузки q_b пере­дающейся на диафрагмы при изгибе оболочки, для разных схем загружения временной (снеговой) нагрузкой и наиболее неблагоприятного влияния усилия предварительного напряжения. Найденная нагрузка сравнивается с несущей способностью оболочки в предельном состоянии, т.е. при ее изломе. Расчет выполняется согласно п. 9.18 - 9.24 [7].

♦ Равномерное загружение панели полной нагрузкой.

Исходные данные для расчета:

полная расчетная нагрузка q = g + s = 3,61 + 1,33 = 4,94 кН / м²; σ_sp = 1,1 · 745 ≈ 820 МПа; γ_sp = 1,1; Р ₂ = 1002 кН; σ_los = 309 МПа; z ₀ = 1135 мм; y ₀ = 372 mm; e _{0 p} = 763 мм; b ₀ = B = 3 м; b ′ _f = 2940 мм; h ′ _f =30 мм; А_sр = 1964 мм²; α = E_s / E_b = 19 · 10⁴ / 29 · 10³ = 6,55.

Вертикальная нагрузка на 1 м², эквивалентная по нормальной силе воздействию усилия обжатия Р ₂:

Коэффициент влияния формы сечения панели

χ = b ′ _fh ′ _fy ₀ z ₀ / I_red = 2940 · 30 · 372 · 1135 / 4619 · 10⁷ = 0,806.

Предельная нагрузка, воспринимаемая панелью в состоянии предельного равновесия (т.е. непосредственно перед разрушением):

Выгиб панели от сил предварительного напряжения

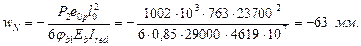
Прогиб панели в предельном состоянии по прочности

Расчетный прогиб панели при нагрузке l,4(g + s)

Расчетная нагрузка на 1 м² приложенная непосредственно к оболочке, с учетом ее собственного веса, но за вычетом веса диафрагм

q_m = (0,75 + 0,0825) · 1,1 + (0,11 + 0,44 + 0,74) + 1,33 = 3,54 кН/м²,

где (0,75 + 0,0825) - вес полки и ее вутов;

(0,11 + 0,44 + 0,74) - вес кровли.

Расчетная изгибающая нагрузка на 1 м², передаваемая на диафрагмы за счет изгиба оболочки:

♦ Загружение постоянной нагрузкой g и снеговой s, располо­женной на левой половине пролета. Исходные данные для расчета точно такие же, как и в предыдущем пункте.

Отношение снеговой и постоянных нагрузок

γ = s / g = 1,33 / 3,61 = 0,37.

Заменяющая нагрузка

q_s = g + s / 2 = 3,61+ 1,33 / 2 = 4,28 кН/м².

Расчетный прогиб панели в середине пролета при действии заменяющей нагрузки q_s приложенная непосредственно к о&° лочке, с учетом ее собственного веса, по за вычетом веса диафрагм

Расчетная изгибающая нагрузка на 1м, передаваемая на диафрагмы при одностороннем загружении оболочки снегом

• На правой половине пролета панели, где снеговая нагрузка отсутствует, создается отрицательная (направленная вверх) изгибающая нагрузка, которую определяем при коэффициенте точности натяжения γ_sp = 0,9; P ₂ = 828 кН; σ_sp = 0,9 · 745 = 670 МПа; σ_los = 249 МПа.

1. Вертикальная нагрузка, эквивалентная по нормальной силе, возни­кающей в оболочке от предварительного напряжения:

2. Выгиб панели от предварительного напряжения

3. Прогиб панели вначале текучести арматуры диафрагм

4. Расчетный прогиб при снеговой нагрузке на левой половине пролета

5. Нагрузка, приложенная непосредственно к оболочке на правой половине пролета (постоянная без учета веса диафрагм)

q_m = 0,916 + 1,29 = 2,2 кН/м².

6. Расчетная изгибающая нагрузка на 1м², передаваемая на диа­фрагмы за счет изгиба оболочки на правой (менее загруженной) половине пролета панели

Таким образом, наибольшая изгибающая нагрузка, передаваемая на диафрагмы, соответствует загружению снегом левой половины пролета и составляет q_{b, max} = q_{b, l} = 0,97 кН/м².

♦ Подбор сечении арматуры оболочки. Момент от наибольшей изгибающей нагрузки q_{b, max} с учетом перераспределения усилий при изломе оболочки

М = q_{b, max}l_оs ² / 16 = 0,97 · 2,2² /16 = 0,293 кНм/м,

где l_оs = 2940 - 2 · (150 + 220) = 2200мм = 2,2 м - пролет оболочки в свету между вутами.

Подберем площадь сечения арматуры на 1 м ширины оболочки, полагая, что армирование будет производиться сеткой из обыкновенной арматурной проволоки Ø5 Bp-I (R_s = 360MПa).

1. h ₀ = h′_f = 30 / 2 = 15 мм.

2.

3.

4. A_s = ξbh ₀ R_b / R_s = 0,089 · 1000 · 15 · 0,9 · 17 / 360 = 56,7мм²/м.

Можно принять 4 Ø5 Bp-I (A_s = 78,5 мм²) с шагом 250 мм. Однако пo п. 5.36 [4] в плитах толщиной до 150 мм шаг стержней должен быть не более 200 мм, поэтому принимаем на 1 м ширины оболочки 5 Ø5 Bp-I с ша­гом 200 мм (A_s = 98,2 мм²); процент армирования µ = 98,2 / 150 = 0,65% > 0,3%. Эта арматура устанавливается в оболочке поперек пролета панели.

В продольном направлении достаточно принять конструктивную арматуру по минимальному проценту армирования

A_s = 0,002 bh ₀ = 0,002 · 1000 · 15 = 30 мм².

Принимаем на 1 м пролета оболочки 5 Ø3 Bp-I (А_s = 36 мм²). Найдем величину предельной изгибающей нагрузки, которую спо­собна воспринять оболочка с принятым армированием

что больше q_{b, max} = 0,97 кН/м, т.е. несущая способность оболочки вполне достаточна.

♦ Проверка прочности сопряжения оболочки с диафрагмой. Проверяются на изгиб сечения 1-1 и 2-2 (рис. 5.20) при действии на обо­лочку расчетных изгибающих нагрузок, найденных выше. Изгибающие мо­менты М_I и М_II в этих сечениях принимаются одинаковыми и определяют­ся по формуле

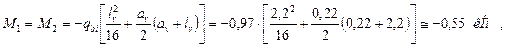
где l_v = l_os = 2200 мм - пролет оболочки между вутами;

a_v = 220 мм - ширина вута оболочки от грани диафрагмы;

q_bi = q_{b, max} = 0,97 кН/м² - расчетная изгибающая нагрузка при наиболее неблагоприятной схеме загружения.

Момент М₁ воспринимается поперечной арматурой сетки оболочки, где на 1 м предусмотрено 5 Ø5 Bp-I (A_s = 98,2 мм²). Тогда предельно момент, воспринимаемый сечением 1-1

 

 

Рис. 5.20. Расчетные сечения для проверки сопряжения оболочки с диафрагмой

 

М _{1, u} = R_bbx (h ₀ - 0,5 x) = 0,9 · 17 · 1000 · 2,3 · (60-0,5 · 2,3) = 2,07 · 10⁶ Hмм = 2,07кНм > M ₁ = 0,55 кНm,

где

h ₀ = h - 15 = 75 - 15 = 60 мм - рабочая высота в сечении 1-1.

Следовательно, несущая способность вута достаточна и дополнительное армирование его не требуется. По конструктивным соображениям в вутах устанавливаем сетки из Ø5 Вр-I.

Момент M ₂ воспринимается вертикальными стержнями - подвеска­ми, расположенными в ребрах жесткости диафрагм (по два стержня Ø10 A-III в каждом ребре). Тогда при b = 12 b ₁ = 12 · 40 = 480 мм (b ₁ = 40 мм - толщина стенки диафрагмы) и h ₀ = 150 / 2 = 75 мм в сечении 2-2 имеем:

высота сжатой зоны бетона

несущая способность сечения

M _{2, u} = γ_{b 2} R_bbx (h ₀ - 0,5 x) = 0,9 · 17 · 480 · 3,9 · (75 – 0,5 · 3,9) = 2,1 · 10⁶ Нмм = 2,1 кНм > М ₂ = 0,55 кНм, т.е. несущая способности сечения 2-2 вполне достаточна.

 

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: