Система массового обслуживания как модель

Родоначальником теории систем массового обслуживания является известный датский ученый А.К.Эрланг (Агнер Краруп) (1878-1929), который, являясь сотрудником Копенгагенской телефонной компании, опубликовал в 1909 г. работу "The Theory of Probabilities and Telephone Conversations" ("Теория вероятностей и телефонные переговоры"), в которой предложил формулы для вычисления количества абонентов АТС, ожидающих соединения с абонентами другой АТС. Работа получила мировое признание, а формулы были взяты на вооружение Главным Почтовым Управлением (General Post Office) Великобритании. Начиная 1940-х гг., единица измерения " Эрланг " принята в качестве меры телекоммуникационного трафика.

Эрланг предложил для описания процессов, происходящих в СМО использовать Марковские процессы с дискретным или конечным множеством состояний.

Случайный процесс, протекающий в системе S, называется Марковским (или «процессом без последействия»), если он обладает следующим свойством: для каждого момента времени t₀ вероятность любого состояния системы в будущем (при t > t₀)зависит только от ее состояния в настоящем (при t= t₀)и не зависит от того, когда и каким образом система пришла в это состояние (т. е. как развивался процесс в прошлом).

Случайный процесс называется процессом с дискретным временем, если переходы системы из состояния в состояние возможны только в строго определенные, заранее фиксированные моменты времени: t₁, t_{2 …} и т. д. В промежутки времени между этими моментами система S сохраняет свое состояние.

Как модель, СМО рассматривается в теории массового обслуживания (другое название − теория очередей). Поскольку первые работы в этой области были вызваны потребностями практики, в частности широким развитием телефонных сетей, то в работах по теории СМО широко используется терминология, заимствованная из телефонии: требования, вызовы, заявки, каналы (приборы) обслуживания и т.п.

Теория массового обслуживания связана с разработкой и анализом математических, т.е. абстрактных, моделей, которые описывают процесс обслуживания некоторых объектов, поступающих на вход обслуживающего прибора в виде некоторого потока, и образующего в общем случае очередь на входе обслуживающего прибора.

Поскольку рассматриваются абстрактные модели, совершенно не важна природа обслуживаемых объектов и их физические свойства (будь то вызовы, управляющие или информационные кадры в сети связи или посетители магазина, или детали на автоматической линии.

Существенным являются моменты появления этих объектов и правила, законы (математические) их обслуживания, так как от этих моментов и законов зависит адекватное отображение эволюции моделируемого объекта во времени. Поэтому, когда говорят о методах анализа очередей, имеют в виду математические (абстрактные) модели, а из контекста всегда должно быть ясно, для исследования какой реальной системы применяются эти модели.

Целью использования СМО как модели является анализ качества функционирования указанных систем оригиналов.

Дадим краткое описание терминов, используемых в СМО.

Заявки (требования) на обслуживание поступают через постоянные или случайные интервалы времени.

Приборы (каналы) служат для обслуживания этих заявок. Обслуживание длится некоторое время, постоянное или случайное. Если в момент поступления заявки все приборы заняты, заявка помещается в ячейку буфера и ждет там начала обслуживания. Заявки, находящиеся в буфере, составляют очередь на обслуживание. Если все ячейки буфера заняты, заявка получает отказ в обслуживании и теряется.

Вероятность потери заявки (вероятность отказа) − одна из основных характеристик СМО.

Другие характеристики:

среднее время ожидания начала обслуживания,

средняя длина очереди,

коэффициент загрузки прибора (доля времени, в течение которого прибор занят обслуживанием) и т.д.

В зависимости от объема буфера различают

· СМО с отказами, где нет буфера,

· СМО с ожиданием, где буфер не ограничен (например, очередь в магазин на улице) и

· СМО смешанного типа, где буфер имеет конечное число заявок.

В СМО с отказами нет очереди, в СМО с ожиданием нет потерь заявок, в СМО смешанного типа то и другое возможно.

Иногда различают заявки по их приоритету, т.е. по важности. Заявки высокого приоритета обслуживаются в первую очередь.

Абсолютный приоритет дает право прервать обслуживание менее важной заявки и занять ее место в приборе (или буфере, если все приборы заняты столь же важными заявками). Вытесненная заявка либо теряется, либо поступает в буфер, где ждет дообслуживания. Иногда приходится возобновлять обслуживание вытесненной заявки с начала, а не продолжать с точки прерывания. Если заявка вытеснена из буфера, она, естественно, теряется. Примером заявки с абсолютным приоритетом является судно, получившее пробоину и нуждающееся в срочной разгрузке.

В вычислительных системах абсолютным приоритетом обладают команды оператора.

Относительный приоритет дает право первоочередного занятия освободившегося прибора. Он не дает право на вытеснение заявки из прибора или буфера. Лица, имеющие льготы при обслуживании в кассе, у врача и т.п., как правило, имеют относительный приоритет.

Абсолютный и относительный приоритеты различаются и моментом действия: абсолютный реализуется в момент поступления, а относительный - в момент освобождения прибора.

Различают фиксированные и динамические приоритеты. Фиксированные приоритеты чаще называют дисциплиной обслуживания.

Дисциплина обслуживания задает порядок выбора из очереди в освободившийся прибор заявок одинакового приоритета. Выделим следующие дисциплины: FIFO (First Input - First Output): первым пришел − первым обслужен, LIFO (Last Input - First Output): последним пришел − первым обслужен, RAND (Random): случайный выбор из очереди.

В быту обычно действует дисциплина FIFO. Дисциплина LIFO реализуется в буфере, организованном по принципу стека. Такая дисциплина может оказаться целесообразной, например, при передаче информации, если ее ценность быстро падает со временем.

Поток событий – последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.

В теории массового обслуживания важным является понятие случайного потока, как некоторой последовательности событий, наступающих в случайные моменты времени.

Поток событий можно наглядно изобразить рядом точек на оси времени O t – рис. 15.2.

Рис.15.2. Изображение потока событий на оси времени

Положение каждой точки случайно, и здесь изображена лишь какая-то одна реализация потока.

Интенсивность потока событий – это среднее число событий, приходящееся на единицу времени.

Рассмотрим некоторые свойства (виды) потоков событий.

1. Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени.

В частности, интенсивность стационарного потока постоянна. Поток событий неизбежно имеет сгущения или разрежения, но они не носят закономерного характера, и среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.

2. Поток событий называется потоком без последствий, если для любых двух непересекающихся участков времени и (см. рис.15.2) число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Другими словами, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга и вызваны каждое своими собственными причинами

3. Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу.

Случайный поток может быть задан функцией распределения величины промежутка (интервала) времени между моментами наступления событий

τ_j = t_j − t_j−1, P(τ_j ≤ t)

В случае P (τ _j ≤ t) = P (τ ≤ t) для всех j ≥2 поток является рекуррентным. Рекуррентный поток, для которого

P (τ ≤ t) = 1 - e ^{(- λ t)}, называется пуассоновским.

Величину λ в случае пуассоновского потока называют интенсивностью потока событий.

Для такого потока вероятность наступления за промежуток времени [0, t ] n событий есть

(t >0, λ >0)

Вероятность непоявления (то есть ни одного, m = 0) события за время τ равна:

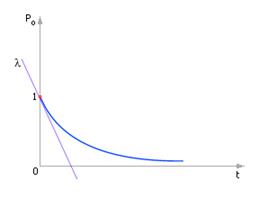
Вероятность появления хотя бы одного события (P _ХБ1С) вычисляется так:

так как P _ХБ1С + P ₀ = 1 (либо появится хотя бы одно событие, либо не появится ни одного, — другого не дано).

Из графика на рис.2 видно, что вероятность появления хотя бы одного события стремится со временем к единице, то есть при соответствующем длительном наблюдении события таковое обязательно рано или поздно произойдет. Чем дольше мы наблюдаем за событием (чем более t), тем больше вероятность того, что событие произойдет — график функции монотонно возрастает.

Чем больше интенсивность появления события (чем больше λ), тем быстрее наступает это событие, и тем быстрее функция стремится к единице. На графике параметр λ представлен крутизной линии (наклон касательной).

Рис. 2.Графи вероятности появления хотя бы одного события со временем

Чем больше интенсивность появления события (чем больше λ), тем быстрее наступает это событие, и тем быстрее функция стремится к единице. На графике параметр λ представлен крутизной линии (наклон касательной).

Математическое ожидание числа событий, наступивших за время t равно λ t, где λ - среднее число событий, наступающих в единицу времени.

Пуассоновский поток называется простейшим, если выполняются условия 1.2.3 то есть этот поток:

· стационарен,

· ординарен,

· не имеет последствий

Простейший поток имеет наиболее простое математическое описание. Он играет среди потоков такую же особую роль, как и закон нормального распределения среди других законов распределения. А именно, при наложении достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.

Для обозначения типа CMО Кендаллом и Башариным предложена система обозначений, имеющих вид Δ|Θ|Σ|Ω. Здесь Δ – обозначение закона распределения вероятностей для интервалов поступления заявок, Θ – обозначение закона распределения вероятностей для времени обслуживания, Σ – число каналов обслуживания, Ω – число мест в очереди.

Обозначение законов распределения в позициях Δ и Θ выполняется обычно буквами из следующего списка:

М – экспоненциальное,

Ek – эрланговское порядка k,

R – равномерное,

D – детерминированное (постоянная величина),

G – произвольное (любого вида) и т.д.

Если число мест в очереди не ограничено, то позиция

Σ не указывается.

Например, M | M | 1 означает простейшую СМО (оба распределения экспоненциальные, канал обслуживания один, очередь не ограничена), а обозначение R | D | 2 | 100 соответствует СМО с равномерным распределением интервалов поступления требований, фиксированным временем их обслуживания, двумя каналами и 100 местами в очереди. В этой СМО заявки, приходящие в моменты, когда все места в очереди заняты, покидают систему (т.е. теряются).

Если в СМО поступает n потоков заявок (у каждого потока свой приоритет), то Δ и Θ приписывают число n в виде индекса. Например, M ₂ | M ₂ | 1 обозначает СМО с двумя потоками заявок, на входе имеющими экспоненциальное распределение, с экспоненциальным временем обслуживания, своим для каждого потока. В системе M ₂ | M |1 время обслуживания всех заявок имеет одно и то же распределение. В случае нескольких входных потоков, имеющих разные приоритеты, необходимо дополнительно указывать типы приоритетов – абсолютные, относительные.

12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: