 |
СМО с отказами (потерями).
|
|
|
|
Простейшей из всех задач теории массового обслуживания является модель одноканальной СМО с отказами (потерями).
При этом система массового обслуживания состоит только из одного канала (n = 1) и на нее поступает пуассоновский поток заявок с интенсивностью λ, зависящей, в общем случае, от времени:
λ = λ(t)
Требуется найти:
1)абсолютную пропускную способность СМО (А);
2)относительную пропускную способность СМО (q).
 |
Рассмотрим единственный канал обслуживания как физическую систему
Рис. 5.6. ГСП для одноканальной СМО с отказами (а); график решения уравнения (5.38) (б)
S, которая может находиться в одном из двух состояний:
S0 — свободен, S1 — занят. ГСП системы показан на рис. 5.6, а.
Из состояния S0 в S1 систему, очевидно, переводит поток заявок с интенсивностью λ; из S1 в S0 — «поток обслуживания» с интенсивностью μ.
Вероятности состояний: p0 и p1. Очевидно, для любого момента t:
p0(t) + p1(t) =1 (5.36)
Напишем алгебраические уравнения Колмогорова для вероятностей состояний. Уравнения строятся в соответствии со следующим правилом.
В левой части каждого уравнения стоит производная вероятности состояния, а правая часть содержит столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния, соответствующий член имеет знак «минус», если в состояние — знак «плюс».
Каждый член равен произведению плотности вероятности перехода, соответствующей данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.
Это правило составления дифференциальных уравнений для вероятностей состояний является общим и справедливо для любой непрерывной марковской цепи; с его помощью можно совершенно механически, без всяких рассуждений, записывать дифференциальные уравнения для вероятностей состояний непосредственно по размеченному графу состояний.
|
|
|
Составим дифференциальные уравнения Колмогорова для вероятностей состояний согласно правилу, данному выше:
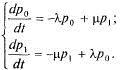
(5.37)
Из двух уравнений (5.37) одно является лишним, так как p0 и p1 связаны соотношением (5.36). Учитывая это, отбросим второе уравнение, а в первое подставим вместо p1 выражение (1- p1 ):
или (5.38)
Поскольку в начальный момент канал свободен, уравнение следует решать при начальных условиях: p0 = 1, p1 =0.
Линейное дифференциальное уравнение (5.38) с одной неизвестной функцией p0 легко может быть решено не только для простейшего потока заявок, (λ=const) но и для случая, когда интенсивность этого потока со временем меняется.
Для первого случая решение есть
Зависимость величины p0 от времени имеет вид, изображенный на рис. 5.6, б. В начальный момент (при t = 0) канал заведомо свободен (p0 (0) = 1). С увеличением t вероятность p0 уменьшается и в пределе (при t=∞) равна 
. Величина, p1(t) дополняющая p0(t) до единицы, изменяется так, как показано на том же рисунке.
Нетрудно убедиться, что для одноканальной СМО с отказами вероятность p0 есть не что иное, как относительная пропускная способность q. Действительно, p0 есть вероятность того, что в момент t канал свободен, или вероятность того, что заявка, пришедшая в момент t, будет обслужена.
В пределе, (при t=∞), когда процесс обслуживания уже установится, предельное значение относительной пропускной способности будет равно:
Зная относительную пропускную способность q, легко найти абсолютную А. Они связаны очевидным соотношением:
В пределе, (при t=∞), абсолютная пропускная способность тоже установится и будет равна
Зная относительную пропускную способность системы q (вероятность того, что пришедшая в момент t заявка будет обслужена), легко найти вероятность отказа:
|
|
|
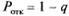
или среднюю часть необслуженных заявок среди поданных. При t=∞
|
|
|
