 |
Потоки Эрланга. Процессы размножения и гибели
|
|
|
|
Математическое исследование СМО очень облегчается, если случайный процесс, протекающий в системе, является марковским. Тогда удается сравнительно просто описать работу СМО с помощью аппарата обыкновенных дифференциальных (в предельном случае — линейных алгебраических) уравнений и выразить в явном виде основные характеристики эффективности обслуживания через параметры СМО и потока заявок.
Важными для практики образцами потоков являются потоки Эрланга. Эти потоки образуются в результате «просеивания» простейших потоков.
Например, если из точек на оси t сохранить не все точки, а только каждую вторую, то в результате такой операции «просеивания» образуется снова поток событий; он называется потоком Эрланга второго порядка.
Вообще, потоком Эрланга к -то порядка называется поток, получающийся, если в простейшем потоке сохранить каждую k -го точку, а остальные выбросить. Очевидно, простейший поток представляет собой частный случай потока Эрланга, а именно поток Эрланга 1 -го порядка.
Интервал времени τ между соседними событиями в потоке Эрланга k -го порядка представляет собой сумму к независимых случайных величин - расстояний между событиями в исходном простейшем потоке:
τ = Στi (i=1..k)
 |
Каждая из этих случайных величин распределена по показательному закону.
Закон распределения интервала T между соседними событиями в потоке называется законом Эрланга k -го порядка.
 |
Нетрудно получить следующие выражения для мат.ожидания, дисперсии и среднего квадратичного отклонения для интервала событий в потоке Эрланга k -го порядка:
Рассмотрим важную разновидность непрерывных марковских цепей — процесс размножения и гибели. Происхождение термина берет начало от биологических задач, где подобной схемой описывается процесс изменения численности популяции [7].
|
|
|
Марковская непрерывная цепь называется «процессом размножения и гибели», если ее ГСП имеет вид, представленный на рис. 5 а, т. е. все состояния можно вытянуть в одну цепочку, в которой каждое из средних состояний (S2,..., S n-1 ) связано прямой и обратной связью с каждым из соседних состояний, а крайние состояния (S1 и Sn) — только с одним соседним состоянием.

Рис. 5. ГСП для процессов размножения и гибели: а — общий вид; б — численный пример
Пример. Техническое устройство состоит из трех одинаковых узлов; каждый из них может выходить из строя (отказывать); отказавший узел немедленно начинает восстанавливаться. Состояния системы:
S1 — все три узла исправны;
S2 — один узел отказал (восстанавливается), два исправны;
S3 —два узла восстанавливаются, один исправен;
S4 —все три узла восстанавливаются.
ГСП показан на рис. 5. б. Из графа видно, что процесс, протекающий в системе, представляет собой процесс размножения и гибели.
Схема размножения и гибели очень часто встречается в самых разнообразных практических задачах; поэтому имеет смысл заранее рассмотреть эту схему в общем виде и решить соответствующую систему алгебраических уравнений с тем, чтобы в дальнейшем, встречаясь с конкретными процессами, протекающими по такой схеме, пользоваться уже готовым решением.
Итак, рассмотрим случайный процесс размножения и гибели с графом состояний, представленным на рис. 5.5, а.
Для первого состояния S1 имеем:
 |
(5.29)
Для второго состояния S2 суммы членов, соответствующих входящим и выходящим стрелкам, равны:
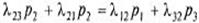
Но, в силу (5.29), можно сократить справа и слева равные друг другу члены и тогда получим:

и далее, совершенно аналогично,  и т. д.
и т. д.
Очевидно, для этого случая члены, соответствующие стоящим друг над другом стрелкам, равны между собой:
|
|
|
 (5.30)
(5.30)
где к принимает все значения от 2 до n.
Итак, предельные вероятности состояний p1, p2,..,pn в любой схеме размножения и гибели удовлетворяют уравнениям:

(5.31)
и нормировочному условию (5.23):
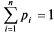
Будем решать эту систему следующим образом: выразим все переменные через p1, а именно:
из первого уравнения (5.31) выразим p2:
 (5.32)
(5.32)
из второго, с учетом (5.32), получим:

и так далее, общая формула имеет вид:
 (5.33)
(5.33)
Эта формула справедлива для любого k от 2 до n.
Обратим внимание на структуру (5.33). В числителе стоит произведение всех интенсивностей (λij), стоящих у стрелок, направленных слева направо, с начала и вплоть до той, которая идет в состояние Sk; в знаменателе — произведение всех интенсивностей (λij), стоящих у стрелок, идущих справа налево, опять-таки, с начала и вплоть до стрелки, исходящей из состояния Sk;. При k = n в числителе будет стоять произведение интенсивностей (λij), стоящих у всех стрелок, идущих слева направо, а в знаменателе — у всех стрелок, идущих справа налево.
Итак, все вероятности p1, p2,..,pn выражены через одну из них: p1. Подставив эти выражения в нормировочное условие и вынося p1 получаем

(5.34)
Остальные вероятности легко выражаются через p1.
Таким образом, задача «размножения и гибели» решена в общем виде: найдены предельные вероятности состояний.
Пример (продолжение). Найти предельные вероятности состояний для процесса размножения и гибели, граф которого показан на рис. 5.4, б.

3.5 Одноканальная СМО
|
|
|


