 |
Одноканальная СМО с ожиданием.
|
|
|
|
Рассмотрим простейшую СМО с ожиданием — одноканальную систему (n - 1), в которую поступает поток заявок с интенсивностью λ; и интенсивность обслуживания μ (т. е. в среднем непрерывно занятый канал будет выдавать λ/μ обслуженных заявок в единицу (времени). Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
С истема с ограниченной длиной очереди. Предположим сначала, что количество мест в очереди ограничено числом m, т. е. если заявка пришла в момент, когда в очереди уже стоят m заявок, она покидает систему необслуженной. В дальнейшем, устремив m к бесконечности, мы получим характеристики одноканальной СМО без ограничений длины очереди.
Будем нумеровать состояния СМО по числу заявок, находящихся в системе (как обслуживаемых, так и ожидающих обслуживания):
S0 —канал свободен;
S1 —канал занят, очереди нет;
S2 — канал занят, одна заявка стоит в очереди;
Sk —канал занят, k - 1 заявок стоят в очереди;
Sm+1 — канал занят, m заявок стоят в очереди.
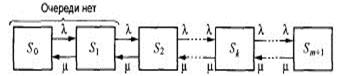
Рис. 5.8. Одноканальная СМО с ожиданием
ГСП показан на рис. 5.8. Все интенсивности потоков событий, переводящих в систему по стрелкам слева направо, равны λ а справа налево — μ. Действительно, по стрелкам слева направо систему переводит поток заявок (как только придет заявка, система переходит в следующее состояние), справа же налево — поток «освобождений» занятого канала, имеющий интенсивность μ (как только будет обслужена очередная заявка, канал либо освободится, либо уменьшится число заявок в очереди).
Изображенная на рис. 5.8 схема представляет собой схему размножения и гибели. Используя общее решение (5.32)—(5.34), напишем выражения для предельных вероятностей состояний (см. также (5.40)):
|
|
|
 (5.44)
(5.44)
или с использованием 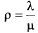 :
:
 (5.45)
(5.45)
Последняя строка в (5.45) содержит геометрическую прогрессию с первым членом 1 и знаменателем ρ; откуда получаем:
 (5.46)
(5.46)
в связи с чем предельные вероятности принимают вид:
 (5.47)
(5.47)
Выражение (5.46) справедливо только при  < 1 (при
< 1 (при 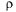 = 1 она дает неопределенность вида 0/0).
= 1 она дает неопределенность вида 0/0).
Определим характеристики СМО: вероятность отказа 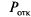 , относительную пропускную способность q, абсолютную пропускную способность А, среднюю длину очереди
, относительную пропускную способность q, абсолютную пропускную способность А, среднюю длину очереди 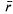 , среднее число заявок, связанных с системой
, среднее число заявок, связанных с системой 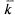 , среднее время ожидания в очереди
, среднее время ожидания в очереди 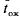 , среднее время пребывания заявки в СМО
, среднее время пребывания заявки в СМО 
Вероятность отказа. Очевидно, заявка получает отказ только в случае, когда канал занят и все m мест в очереди тоже:
 (5.48)
(5.48)
Относительная пропускная способность:
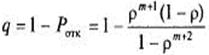 (5.49)
(5.49)
Абсолютная пропускная способность:
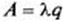
Средняя длина очереди. Найдем среднее число  заявок, находящихся в очереди, как математическое ожидание дискретной случайной величины R — числа заявок, находящихся в очереди:
заявок, находящихся в очереди, как математическое ожидание дискретной случайной величины R — числа заявок, находящихся в очереди:

С вероятностью  в очереди стоит одна заявка, с вероятностью
в очереди стоит одна заявка, с вероятностью 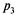 — две заявки, вообще с вероятностью
— две заявки, вообще с вероятностью 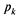 в очереди стоят k - 1 заявок, и т. д., откуда:
в очереди стоят k - 1 заявок, и т. д., откуда:
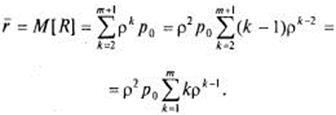 (5.50)
(5.50)
Поскольку 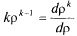 , сумму в (5.50) можно трактовать как производную по
, сумму в (5.50) можно трактовать как производную по 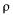 от суммы геометрической прогрессии:
от суммы геометрической прогрессии:

Подставляя данное выражение в (5.50) и используя  из (5.47), окончательно получаем:
из (5.47), окончательно получаем:
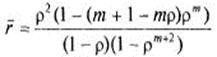 (5.51)
(5.51)
Среднее число заявок, находящихся в системе. Получим далее формулу для среднего числа 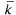 заявок, связанных с системой (как стоящих в очереди, так и находящихся на обслуживании). Поскольку
заявок, связанных с системой (как стоящих в очереди, так и находящихся на обслуживании). Поскольку 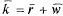 , где_
, где_ 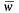 — среднее число заявок, находящихся под обслуживанием, а r известно, то остается определить
— среднее число заявок, находящихся под обслуживанием, а r известно, то остается определить 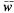 . Поскольку канал один, число обслуживаемых заявок может равняться 0 (с вероятностью
. Поскольку канал один, число обслуживаемых заявок может равняться 0 (с вероятностью  ) или 1 (с вероятностью 1 -
) или 1 (с вероятностью 1 -  ), откуда:
), откуда:
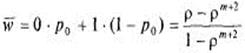
и среднее число заявок, связанных с СМО, равно
 (5.52)
(5.52)
Среднее время ожидания заявки в очереди. Обозначим его 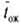 ; если заявка приходит в систему в какой-то момент времени, то с вероятностью
; если заявка приходит в систему в какой-то момент времени, то с вероятностью 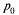 канал обслуживания не будет занят, и ей не придется стоять в очереди (время ожидания равно нулю). С вероятностью
канал обслуживания не будет занят, и ей не придется стоять в очереди (время ожидания равно нулю). С вероятностью 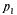 она придет в систему во время обслуживания какой-то заявки, но перед ней не будет очереди, и заявка будет ждать начала своего обслуживания в течение времени
она придет в систему во время обслуживания какой-то заявки, но перед ней не будет очереди, и заявка будет ждать начала своего обслуживания в течение времени  (среднее время обслуживания одной заявки). С вероятностью
(среднее время обслуживания одной заявки). С вероятностью 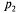 в очереди перед рассматриваемой заявкой будет стоять еще одна, и время ожидания в среднем будет равно
в очереди перед рассматриваемой заявкой будет стоять еще одна, и время ожидания в среднем будет равно 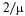 , и т. д.
, и т. д.
|
|
|
Если же k = m + 1, т. е. когда вновь приходящая заявка застает канал обслуживания занятым и m заявок в очереди (вероятность этого 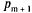 ), то в этом случае заявка не становится в очередь (и не обслуживается), поэтому время ожидания равно нулю. Среднее время ожидания будет равно:
), то в этом случае заявка не становится в очередь (и не обслуживается), поэтому время ожидания равно нулю. Среднее время ожидания будет равно:

если подставить сюда выражения для вероятностей (5.47), получим:
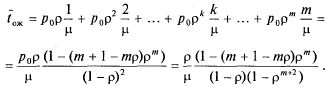 (5.53)
(5.53)
Здесь использованы соотношения (5.50), (5.51) (производная геометрической прогрессии), а также  из (5.47). Сравнивая это выражение с (5.51), замечаем, что иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
из (5.47). Сравнивая это выражение с (5.51), замечаем, что иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
 (5.54)
(5.54)
Среднее время пребывания заявки в системе. Обозначим  матожидание случайной величины — время пребывания заявки в СМО, которое складывается из среднего времени ожидания в очереди
матожидание случайной величины — время пребывания заявки в СМО, которое складывается из среднего времени ожидания в очереди 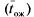 и среднего времени обслуживания
и среднего времени обслуживания 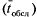 . Если загрузка системы составляет 100 %, очевидно,
. Если загрузка системы составляет 100 %, очевидно,  , в противном же случае
, в противном же случае
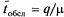
Отсюда
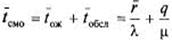
Пример 5.6. Автозаправочная станция (АЗС) представляет собой СМО с одним каналом обслуживания (одной колонкой).
Площадка при станции допускает пребывание в очереди на заправку не более трех машин одновременно (m = 3). Если в очереди уже находятся три машины, очередная машина, прибывшая к станции, в очередь не становится. Поток машин, прибывающих для заправки, имеет интенсивность 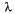 = 1 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин.
= 1 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин.
Определить:
вероятность отказа;
относительную и абсолютную пропускную способности АЗС;
среднее число машин, ожидающих заправки;
среднее число машин, находящихся на АЗС (включая обслуживаемую);
среднее время ожидания машины в очереди;
среднее время пребывания машины на АЗС (включая обслуживание).
|
|
|
иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.
Находим вначале приведенную интенсивность потока заявок:
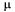 = 1/1,25 = 0,8;
= 1/1,25 = 0,8;  =1/0,8 = 1,25.
=1/0,8 = 1,25.
По формулам (5.47):
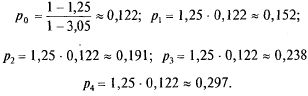
p0 = (1-1.250) / (1-3.05)=0.122 p1 = 1.25*0.122=0.152
p2 =0.152*1.25=0.19 p3 = 0.19*1.25=0.238 p4 =0.238*1.25 =0.296
Вероятность отказа  0,296.
0,296.
Относительная пропускная способность СМО
q=1-  =0,704.
=0,704.
Абсолютная пропускная способность СМО
A = 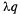 = 0,704 машины в мин.
= 0,704 машины в мин.
Среднее число машин в очереди находим по формуле (5.51)

т. е. среднее число машин, ожидающих в очереди на заправку, равно 1,56.
Прибавляя к этой величине среднее число машин, находящихся под обслуживанием
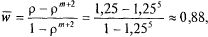
получаем среднее число машин, связанных с АЗС.
Среднее время ожидания машины в очереди по формуле (5.54)
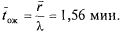
Прибавляя к этой величине 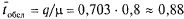 , получим среднее время, которое машина проводит на АЗС:
, получим среднее время, которое машина проводит на АЗС:

Системы с неограниченным ожиданием. В таких системах значение m не ограничено и, следовательно, основные характеристики могут быть получены путем предельного перехода 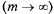 в ранее полученных выражениях (5.44), (5.45) и т. п.
в ранее полученных выражениях (5.44), (5.45) и т. п.
Заметим, что при этом знаменатель в последней формуле (5.45) представляет собой сумму бесконечного числа членов геометрической прогрессии. Эта сумма сходится, когда прогрессия бесконечно убывающая, т. е. при 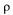 < 1.
< 1.
Может быть доказано, что 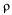 < 1 есть условие, при котором в СМО с ожиданием существует предельный установившийся режим, иначе такого режима не существует, и очередь при
< 1 есть условие, при котором в СМО с ожиданием существует предельный установившийся режим, иначе такого режима не существует, и очередь при 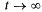 будет неограниченно возрастать. Поэтому в дальнейшем здесь предполагается, что
будет неограниченно возрастать. Поэтому в дальнейшем здесь предполагается, что 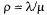 < 1.
< 1.
Если 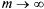 , то соотношения (5.47) принимают вид:
, то соотношения (5.47) принимают вид:
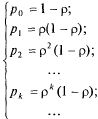 (5.55)
(5.55)
При отсутствии ограничений по длине очереди каждая заявка, пришедшая в систему, будет обслужена, поэтому q = 1,
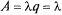
Среднее число заявок в очереди получим из (5.51) при  :
:

Среднее число заявок в системе по формуле (5.52) при 
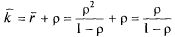
Среднее время ожидания 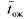 получим из формулы
получим из формулы
(5.53) при 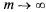 :
:
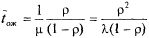
Наконец, среднее время пребывания заявки в СМО есть
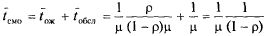
|
|
|


