 |
Многоканальная СМО с ожиданием
|
|
|
|
Система с ограниченной длиной очереди. Рассмотрим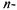 
канальную СМО с ожиданием, на которую поступает поток заявок с интенсивностью 
; интенсивность обслуживания (для одного канала) 
; число мест в очереди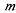 
.
Состояния системы нумеруются по числу заявок, связанных системой:
нет очереди:
—все каналы свободны;
— занят один канал, остальные свободны;
— заняты 
каналов, остальные нет;
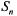— заняты все 
каналов, свободных нет;
есть очередь:
—заняты все n каналов; одна заявка стоит в очереди;
— заняты все n каналов, r заявок в очереди;
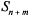—заняты все n каналов, m заявок в очереди.
ГСП приведен на рис. 5.9. У каждой стрелки проставлены соответствующие интенсивности потоков событий. По стрелкам слева направо систему переводит всегда один и тот же поток заявок с интенсивностью 
, по стрелкам справа налево систему переводит поток обслуживании, интенсивность которого равна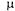 
, умноженному на число занятых каналов.
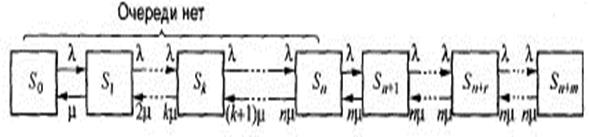
Многоканальная экспоненциальная СМО отличается от одноканальной следующим. Число каналов в ней более одного. Приходящая заявка становится в очередь, если все каналы заняты. В противном случае заявка занимает свободный канал. 
(5.56)
Напишем выражения для предельных вероятностей состояний, используя обозначение 
: (см.5.45)
Вероятность отказа. Поступившая заявка получает отказ, если заняты все n каналов и все m мест в очереди:
(5.57)
Относительная пропускная способность дополняет вероятность отказа до единицы:
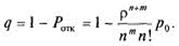
Абсолютная пропускная способность СМО:
(5.58)
Среднее число занятых каналов. Для СМО с отказами оно совпадало со средним числом заявок, находящихся в системе. Для СМО с очередью среднее число занятых каналов не совпадает со средним числом заявок, находящихся в системе: последняя величина отличается от первой на среднее число заявок, находящихся в очереди.
|
|
|
Обозначим среднее число занятых каналов 
. Каждый занятый канал обслуживает в среднем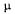 
заявок в единицу времени, а СМО в целом обслуживает в среднем А заявок в единицу времени. Разделив одно на другое, получим:
Среднее число заявок в очереди можно вычислить непосредственно как математическое ожидание дискретной случайной величины:
(5.59)
где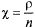 
Здесь опять (выражение в скобках) встречается производная суммы геометрической прогрессии (см. выше (5.50), (5.51)—(5.53)), используя соотношение для нее, получаем:
Среднее число заявок в системе:
Среднее время ожидания заявки в очереди. Рассмотрим ряд ситуаций, различающихся тем, в каком состоянии застанет систему вновь пришедшая заявка и сколько времени ей придется ждать обслуживания.
Если заявка застанет не все каналы занятыми, ей вообще не придется ждать (соответствующие члены в математическом ожидании равны нулю). Если заявка придет в момент, когда заняты все п каналов, а очереди нет, ей придется ждать в среднем время, равное 
(потому что «поток освобождений»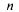 
каналов имеет интенсивность 
). Если заявка застанет все каналы занятыми и одну заявку перед собой в очереди, ей придется в среднем ждать в течение времени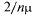 
(по 
на каждую впереди стоящую заявку) и т. д. Если заявка застанет в очереди 
заявок, ей придется ждать в среднем в течение времени 
. Если вновь пришедшая заявка застанет в очереди уже m заявок, то она вообще не будет ждать (но и не будет обслужена).
Среднее время ожидания найдем, умножая каждое из этих значений на соответствующие вероятности:
(5.60)
Так же, как и в случае одноканальной СМО с ожиданием, отметим, что это выражение отличается от выражения для средней длины очереди (5.59) только множителем 
, т. е.
Среднее время пребывания заявки в системе, так же, как и для одноканальной СМО, отличается от среднего времени ожидания на среднее время обслуживания, умноженное на относительную пропускную способность:
|
|
|
Системы с неограниченной длиной очереди.
Мы рассмотрели 
канальную СМО с ожиданием, когда в очереди одновременно могут находиться не более m заявок.
Так же, как и ранее, при анализе систем без ограничений необходимо рассмотреть полученные соотношения при 
.
Вероятности состояний получим из формул (5.56) предельным переходом (при 
). Заметим, что сумма соответствующей геометрической прогрессии сходится при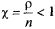 
и расходится при 
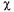> 1. Допустив, что 
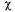< 1 и устремив в формулах (5.56) величину m к бесконечности, получим выражения для предельных вероятностей состояний:
(5.61)
Вероятность отказа, относительная и абсолютная пропускная способность. Так как каждая заявка рано или поздно будет обслужена, то характеристики пропускной способности СМО составят:
Среднее число заявок в очереди получим при 
из (5.59):
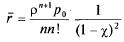
а среднее время ожидания — из (5.60):
Среднее число занятых каналов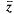 
, как и ранее, определяется через абсолютную пропускную способность:
Среднее число заявок, связанных с СМО, определяется как среднее число заявок в очереди плюс среднее число заявок, находящихся под обслуживанием (среднее число занятых каналов):
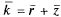
Усложнение структур и режимов реальных систем затрудняет применение классических методов теории массового обслуживания ввиду возрастающей размерности решаемых задач, что особенно характерно для систем с сетевой структурой. Одним из возможных путей преодоления размерности является использование моделей в форме сетей массового обслуживания (СеМО).
СеМО представляет собой совокупность конечного числа обслуживающих узлов, в которой циркулируют заявки, переходящие в соответствии с маршрутной матрицей из одного узла в другой. Узел всегда является разомкнутой СМО. При этом отдельные СМО отображают функционально самостоятельные части реальной системы, связи между СМО − структуру системы, а требования, циркулирующие по СеМО, − составляющие материальных потоков (сообщения (пакеты) в коммуникационной сети, задания в мультипроцессорных системах, контейнеры грузопотоков и т.п.).
|
|
|
В свою очередь, СеМО используют для определения важнейших системных характеристик информационных систем: производительности; времени доставки пакетов; вероятности потери сообщений и блокировки в узлах; области допустимых значений нагрузки, при которых обеспечивается требуемое качество обслуживания и др.
В теории СеМО фундаментальным является понятие состояния сети. Важнейшая характеристика сетей МО − вероятности их состояний. Для определения вероятностей состояний СеМО исследуют протекающий в сети случайный процесс. В качестве моделей протекающих в СеМО процессов также наиболее часто используют марковские и полумарковские.
3.3. Система массового обслуживания как модель
1.5. Сети массового обслуживания
Марковским процессом с непрерывным временем описывают функционирование экспоненциальных СеМО.
Сеть называется экспоненциальной, если входящие потоки требований в каждую СМО пуассоновские, а времена каждого этапа обслуживания, реализуемого на любой СМО сети, имеют экспоненциальное распределение. Это позволяет считать, что этапы обслуживания независимы между собой и не зависят ни от параметров входящего потока, ни от состояния сети, ни от маршрутов следования требований.
Теория экспоненциальных СеМО наиболее разработана, и ее широко применяют как для исследования сетей ПД так и для исследования мультипроцессорных вычислительных систем (ВС). Разработаны практические формулы расчета вероятностно-временных характеристик (ВВХ) таких сетей и систем.
Попытки глубокого анализа немарковских моделей сетевых систем наталкиваются на значительные трудности, которые обусловлены в частности отсутствием независимости длительностей пребывания требований в различных узлах моделей сетевых систем с нестандартными дисциплинами. Так, например, при достаточно реалистическом предположении о том, что длина требования остается постоянной в процессе его передачи через узлы сети, необходимо прослеживать путь каждого требования, что делает невозможным аналитический расчет характеристики для сети с числом узлов М>2.
|
|
|
Анализ работ, посвященных исследованию или расчету немарковских моделей, показывает, что решения, как правило, получены алгоритмически путем сложных численных расчетов с использованием преобразований Лапласа-Стилтьеса, реализуются программно, отличаются большой трудоемкостью, либо значительными погрешностями в оценке показателей производительности информационных систем (ИС) в области средней и большой нагрузки. Поэтому для моделирования СеМО, выходящих из класса мультипликативных, используют приближенные методы.
Сравнительный анализ приближенных методов моделирования СеМО и примеры, приведенные в [1-5] показывают, что пользоваться приближенными методами расчета СеМО необходимо с большой осторожностью, что при расчете конкретных СеМО, в процессе решения различных прикладных задач представляется необходимым проведение исследований в целях оценки точности и чувствительности применяемого метода, а также проведение эксперимента по имитационному моделированию исходной СеМО для достаточно большого множества значений варьируемых параметров.
Аналитические методы расчета характеристик ИС базируются, как правило, на анализе экспоненциальных СеMO. При использовании этого математического аппарата удается получить аналитические модели для решения широкого круга задач исследования систем. CеМО − это, прежде всего, совокупность взаимосвязанных систем массового обслуживания. Поэтому необходимо вспомнить основные особенности этих систем.
Сеть массового обслуживания представляет собой совокупность конечного числа N обслуживающих узлов, в которой циркулируют заявки, переходящие в соответствии с маршрутной матрицей из одного узла в другой. Узел всегда является разомкнутой СМО (причем СМО может быть любого класса). При этом отдельные СМО отображают функционально самостоятельные части реальной системы, связи между СМО - структуру системы, а требования, циркулирующие по СеМО, - составляющие материальных потоков (сообщения (пакеты) в коммуникационной сети, задания в мультипроцессорных системах, контейнеры грузопотоков и т.п.).
Для наглядного представления СеМО используется граф, вершины которого (узлы) соответствуют отдельным СМО, а дуги отображают связи между узлами.
Переход заявок между узлами происходит мгновенно в соответствии с переходными вероятностями 
, pij - вероятность того, что заявка после обслуживания в узле i перейдет в узел j. Естественно, если узлы непосредственно не связаны между собой, то pij = 0. Если из i- го узла переход только в один какой-либо узел j, то pij = 1.
|
|
|
СеМО классифицируют по нескольким признакам (рис. 4).
Сеть называется линейной, если интенсивности потоков заявок в узлах связаны между собой линейной зависимостью
l j = a ij l i,
где a ij - коэффициент пропорциональности, или относительно источника
l j = a j l 0,.
Коэффициент a j называют коэффициентом передачи, он характеризует долю заявок, поступающих в j- й узел от источника заявок, либо - среднее число прохождений заявкой через данный узел за время нахождения заявки в сети.
Если интенсивности потоков заявок в узлах сети связаны нелинейной зависимостью (например, 
), то сеть называется нелинейной..
Сеть всегда линейна, если в ней заявки не теряются и не размножаются.
Разомкнутая сеть – это такая отрытая сеть, в которую заявки поступают из внешней среды и уходят после обслуживания из сети во внешнюю среду. Другими словами, особенностью разомкнутой СеМО (РСеМО) является наличие одного или нескольких независимых внешних источников, которые генерируют заявки, поступающие в сеть, независимо от того, сколько заявок уже находится в сети. В любой момент времени в РСеМО может находиться произвольное число заявок (от 0 до ¥).
Рис. 4. Классификация сетей массового обслуживания
В замкнутой СеМО (ЗСеМО) циркулирует фиксированное число заявок, а внешний независимый источник отсутствует. Исходя из физических соображений, в ЗСеМ О выбирается внешняя дуга, на которой отмечается псевдонулевая точка, относительно которой могут измеряться временные характеристики.
Комбинированная сеть – это сеть, в которой постоянно циркулирует определенное число заявок и есть заявки, поступающие от внешних независимых источников.
В однородной сети циркулируют заявки одного класса. И, наоборот, в неоднородной сети могут присутствовать заявки нескольких классов. Заявки относятся к разным классам, если они различаются хотя бы одним из следующих атрибутов:
- законом распределения длительности обслуживания в узлах;
- приоритетами;
- маршрутами (путями движения заявок в сети).
В экспоненциальной сети длительности обслуживания во всех узлах распределены по экспоненциальному закону, и потоки, поступающие в разомкнутую сеть, простейшие (пуассоновские). Во всех остальных случаях сеть является неэкспоненциальной.
Если хотя бы в одном узле осуществляется приоритетное обслуживание, то это – приоритетная сеть. Приоритет – это признак, определяющий очередность обслуживания. Если обслуживание заявок в узлах осуществляется в порядке поступления, то такая сеть бесприоритетная.
Таким образом, экспоненциальной будем называть СеМО, отвечающую требованиям:
- входные потоки СеМО пуассоновские;
- во всех N СМО время обслуживания заявок имеет экспоненциальную функцию распределения вероятностей, и заявки обслуживаются в порядке прихода;
- переход заявки с выхода i -й СМО на вход j -й является независимым случайным событием, имеющим вероятность pij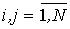 
; pi0 - вероятность ухода заявки из CeМО.
Если заявки приходят в сеть и уходят из нее, то сеть называется разомкнутой. Если заявки не приходят в сеть и из нее не уходят, сеть называется замкнутой. Число заявок в замкнутой сети постоянное.
|
|
|
