 |
Свойства разомкнутой экспоненциальной СеМО
|
|
|
|
Повторим определение сети массового обслуживания.
Входным потоком заявок СМО будем называть поток заявок, приходящих на вход отдельной СМО из внешней среды СеМО, т.е. не с выхода какой-либо СМО. В общем случае число входных потоков СеМО равно числу СМО.
Разомкнутая экспоненциальная СеМО задается следующими параметрами:
1) числом N СМО;
2) числом К 1,..., KN каналов в СМО 1,…, N;
3) матрицей Р = || pij || вероятностей передач, i = 1,…, N; j =0,…, N;
4) интенсивностями I 1,..., IN входных потоков заявок;
5) средними временами обслуживания 
,..., 
заявок в СМО.
Например, СеМО (рис. 5) будет задана численно в следующем виде:
Рис. 5 Сеть массового обслуживания
С помощью СеМО можно промоделировать, например, вычислительную систему [6] в РИСУ. Тогда входные потоки заявок СеМО будут изображать запросы, поступающие на вход вычислительной системы, отдельные СМО будут соответствовать этапам их обработки на устройствах (процессорах, периферийных устройствах и др.), выходные заявки СеМО - результатам обработки запросов.
В экспоненциальной СеМО поток заявок на входе СМО складывается из входного потока СеМО (возможно, имеющего нулевую интенсивность) и из потоков, поступающих с выходов СМO. Входной поток СМO в экспоненциальной СеМО в общем случае непуассоновский. Это значит, что СМО в ней в общем случае не экспоненциальные. Тем не менее достаточно часто считают, что СМO ведут себя в ней во многом как экспоненциальные. В частности, характеристики СМО отвечают (1.2) - (1.13). Поэтому для их расчета в заданной СеМО достаточно найти интенсивности l1,...,l N входных потоков СМО.
Нахождение интенсивностей l1,...,l N осуществляется на основе уравнений баланса сети с учетом простых свойств слияния и разветвления потоков.
|
|
|
При слиянии n потоков заявок с интенсивностями l1,...,l n образуется поток, имеющий интенсивность l = l1+,...,+l n. При ветвлении потока с интенсивностью l на n направлений, вероятности перехода заявки в которые равны р 1,..., рn, образуется n потоков c интенсивностями l р 1,..., l рn соответственно.
В стационарной СеМО среднее число заявок в любой ее фиксированной части постоянное. Отсюда следует, что суммарная интенсивность входящих в эту часть потоков равна суммарной интенсивности выходящих. Запись данного закона в математической форме называется уравнением баланса. Выделяя различные части в СеМО и составляя для них уравнения баланса, можно получить систему уравнений, связывающую неизвестные интенсивности l1,...,l N c известными I 1,.., IN . Обычно при этом в качестве отдельных частей СеМО выделяют все СМО. В этом случав для N неизвестных имеется N уравнений. Можно добавить к ним уравнение баланса для входных и выходных потоков всей СеМО. Тогда получится N +1 уравнение, и одно из них можно использовать в качестве проверочного.
Например, баланс интенсивностей в сети для рис. 5 можно учесть, обозначая интенсивности на входах и выходах СМО и СеМО так, как показано на рис.6. Применяя свойства слияния и ветвления потоков, запишем, что
| l 1= I 1 + l2 + l3 I 1 = P 10·l1 l2 = P 12·l1 l3 = P 13·l1 | (2.1) |
Рис. 6. Баланс интенсивностей
При известных I 1=1, р 1=0,1; р 2=0,5; р 3=0,4 из последних трёх уравнений находим l1=10, l2=5, l3=4. Используя первое уравнение в (2.1) для проверки, подставляем в него найденные значения интенсивностей и получаем тождество 10=1+5+4, подтверждающее правильность произведённых вычислений.
Проверка стационарности СеМО
СеМО стационарна, если стационарны все СМО, т.е. если
(2.2)
Проверить эти условия после того, как определены, l j , не представляет труда. Например, для СеМО (рис. 6) (2.2) выполняется, поскольку 
Для стационарной экспоненциальной СеМО с известными интенсивностями l j расчёт локальных характеристик сводится к применению (1.2) - (1.13).
|
|
|
Например, для СеМО (рис. 6) находим, что
ρ1= 0,7;
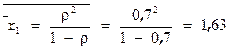- средняя длина очереди в СМО1
- среднее число заявок в СМО1
ρ2=0,3; r2=0,13; k 2=0,43; 
=0,026; 
=0,086; ρ3= 0,7; b0=0,176; r3=0,402; k 3= 1,802; 
=0,1; 
=0,45.
|
|
|
