 |
Определение оптимальной стратегии обслуживания ЛА методом динамического программирования
|
|
|
|
Вариант 3
Исходные данные:
| Исходные величины | Значения |
| Срок эксплуатации взаимно удаленных объектов, лет m | |
| Количество доставляемого компонента топлива,M0, единиц | |
| Коэффициент в функции доставки первым способом, k3 | 0,13 |
| Коэффициент в функции стоимости, k4 | 0,145 |
| Коэффициент в функции стоимости, k1 | |
| Коэффициент в функции стоимости, k2 | |
| Свободный член в функции стоимости, с1 | |
| Свободный член в функции стоимости, с2 | |
| Показатель степени в функции стоимости n1 | |
| Показатель степени в функции стоимости n2 |
Постановка задачи
Имеется определенное количество продукта (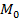
), которое необходимо доставить к обслуживаемым объектам за m лет эксплуатации этих объектов. Доставка производится как с помощью общего стационарного агрегата, так и с помощью индивидуальных стационарных агрегатов. Полезная нагрузка, транспортируемая к объектам с помощью любого агрегата требует ежегодных вложений (расходов), зависящих от того, сколько продукта какая система доставила. Если X продукта доставляется с помощью общего стационарного агрегата, то за год будет израсходовано f(X) средств: при этом не весь продукт может быть доставлен к концу года, так что к началу следующего года от него останется какая-то часть 
. Аналогично, для доставки продукта Y с помощью стационарных агрегатов индивидуального обслуживания, необходимо израсходовать g(Y) средств, а к концу года останется от продукта какая-то часть 
. По истечении года, оставшийся от 
продукт заново распределяется между средствами доставки. Дополнительного продукта извне не поступает. Требуется найти такой способ обслуживания объектов (какие объекты какими агрегатами обслуживать в разные годы), при котором суммарные расходы будут минимальны.
|
|
|
Схема решения задачи.
Поставленную задачу целесообразно решать методом динамического программирования по следующей схеме.
Рассматриваемая система S в данном случае – два способа доставки продукта к объектам обслуживания. Она характеризуется двумя параметрами X и Y, выражающими количество продукта, доставляемого к объектам стационарным агрегатом общего пользования и индивидуальными агрегатами стационарного базирования. Естественным «шагом» управления является финансовый год.
Выражения, связывающие между собой массу доставляемого компонента со стоимостью представим в виде:
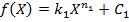
Количество компонента, которое необходимо доставить к объектам за один год, известно, поэтому функции 
могут быть заданы, например, в таком виде:
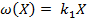
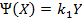
Требуется выбрать способ заправки компонента топлива взаимно удаленных объектов, исходя из минимума затрат. Решение поставленной задачи может быть выполнено методом динамического программирования, следующим образом:
Расход средств на i-ом шаге будет
(*)
Под влиянием этого управления 
доставки компонента общим агрегатом система на i-ом шаге перейдет из состояния 
в состояние
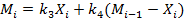
где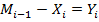 
Основное функциональное управление имеет вид:
( 
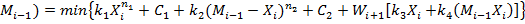
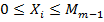
Это означает, что min берется по всем неотрицательным величинам Xi, не превосходящим наличного запаса продукта Mi-1.
Условным оптимальным управлением на i-м шаге будет то из значений Xi, при котором выражение в фигурных скобках достигает минимума.
Условная оптимальная доставка компонента на последнем шаге в последний год эксплуатации будет определяться минимальным значением функции (*)
W4 (M3) = min[W4(M3X4)] = min [k1X4n1 + C1 + k2(M3-X4)n2 + C2]
0 ≤ X4 ≤ M3
Берем первую производную и приравняем к нулю:
k1n1X4n1-1 - k2n2(M3-X4)n2-1 = 0
= 0
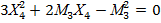
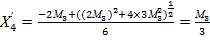
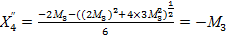– корень не удовлетворяет условию
|
|
|
Условное оптимальное управление на 5м шаге имеет вид:
W4 (M3X4) = 4*(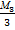
)2 + 2*(
)3 + 155
Основное функциональное управление:
W4 (M3) = min {k1X4n1 + C1 + k2(M3-X4)n2 + C2 + W4[k3X4 + k4(M3-X4)]}
W4 (M3) = min {4X42 + 85 + 2(M3-X4)3 + 70+W4[0,13X4 + 0,145(M3-X4)]}
W3 (M2) = min {4X32 + 85 + 2(M2-X3)3 +70+ W3[0,13X3 + 0,145(M2-X3)]}
W2 (M1) = min {4X22 + 85 + 2(M1-X2)3 +70+ W2[0,13X2 + 0,145(M1-X2)]}
W1 (M0) = min {4X12 + 85 + 2(M0-X1)3 + 70+W1[0,13X1 + 0,145(M0-X1)]}
Подставляя M0 в данные выражения, находим искомые Xi, Wi для всех 5 шагов:
W1(M0Х1)=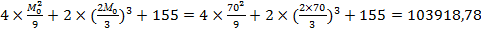 
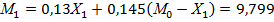
W2(M1X2) = 
= 8907,08
Х2=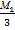 
=3,26
M2 = 
W3(M2X3) = 
X3 =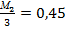 
M3 =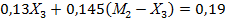 
W4(M3X4) =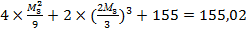 
X4 =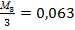 
M4 = 
0,026
Совокупность продукта, доставляемого стационарным агрегатом общего пользования по годам
X = (X1, X2, …, Xm)
X = (23,333; 3,26; 0,45; 0,063)
будет представлять собой оптимальное управление, наряду с которым имеет место
Y = (Y1, Y2, …, Ym) = (M0 – X1, M1* - X2, … Mm-1* - Xm)
Y = (46,667; 6,539; 0,91; 0,127)
- количество продукта, доставляемого стационарными агрегатами индивидуального пользования по годам.
Башня обслуживания
Основное назначение башни обслуживания — обеспечение предстартовой подготовки ЛА при нахождении его в вертикальном положении на ТП и СП. Башни обслуживания могут быть как передвижными, так и стационарными.
Передвижные башни способны двигаться по рельсовым путям на расстояния, обеспечивающие их сохранность при пуске или аварии ЛА.
Поворотные башни применяются для обслуживания ЛА в одной плоскости. Перед пуском эти башни поворачиваются по кольцевому рельсу вокруг центральной опоры на угол, обеспечивающий их сохранность.
Стационарные башни обслуживания монтируются на пусковой системе или рядом с ней. Такие башни оборудованы специальными рабочими площадками, на которых размещаются необходимые электропневмогидросистемы. Перед пуском ЛА или в момент пуска они отводятся на безопасное расстояние.
На башню обслуживания в основном действуют нагрузки от массы площадок, вспомогательного оборудования и ветровые нагрузки.
Высота башни обслуживания определяется длиной ЛА и составляет
,
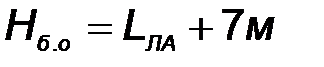где 
— полная длина ЛА.
|
|
|
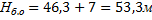
