Д. Разбивка проектной продольной оси в подземных выработках и сооружениях

11.24. Разбивка проектной оси сооружения от полигонометрических знаков на прямых участках трассы выполняется следующими способами:

а) откладыванием смещений d от полигонометрических знаков до проектной оси;

б) выносом от полигонометрических знаков линий, параллельных проектной оси;

в) выносом от полигонометрических знаков осевых отвесов полярным способом.

11.25. Детальную разбивку проектной оси в пределах переходной кривой производят либо от линии тангенса, либо от стягивающей эту кривую хорды.

11.26. Вынос в натуру от линии тангенса точек на переходной кривой производят откладыванием абсцисс х и ординат y.

При разбивке оси пути пользуются формулами:

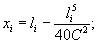
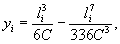
где l_i - длина кривой от НПК₁ до точки i.

С - параметр переходной кривой.

При разбивке оси тоннеля откладывается ордината y_i = y_i + q_i; q_i определяется по формуле

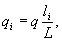
где L - длина всей переходной кривой.

11.27. Большую точность дает метод разбивки переходной кривой от стягивающей ее хорды (рис. 11.13), так как промеры от хорды до переходной кривой значительно короче, чем промеры от тангенса.

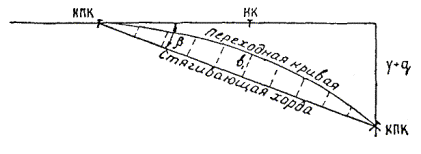
Рис. 11.13.Разбивка переходной кривой с помощью стягивающей хорды

Угол b между линией тангенса и стягивающей хордой получают из разности их дирекционных углов или по формуле

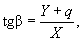
где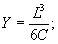

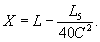
Величина стрелы прогиба b_i переходной кривой по оси тоннеля определяется по приближенной формуле

b_i = l_i tg b - (y_i + q_i).

где l_i - расстояние по хорде от начала первой переходной кривой или от конца второй переходной кривой до проекции точки i на хорду.

При больших длинах переходных кривых размеры стрел прогиба можно значительно уменьшить разбивкой от двух стягивающих хорд (рис. 11.14).

Угол b₁ (составленный направлением первой хорды с линией тангенса) и угол b₂ (составленный продолжением первой хорды и направлением второй) вычисляются по разностям дирекционных углов, полученным из решения обратных задач. Углы b₁ и b₂ могут быть проверены по приближенным формулам:

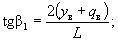
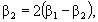
где b - угол между линией тангенса и хордой, стягивающей всю переходную кривую.

Для первой хорды стрелы прогиба b _{1 i} вычисляются по формуле

b _{1 i} = l _{1 i} tg b₁ - (y_i + q_i);

для второй хорды стрелы прогиба b _{2 i} определяются по формуле

b _{2 i} = l _{1 i} tg b₁ + l _{2 i} tg b₂ - (y_i + q_i);

В указанных формулах:

l _{1 i} - расстояние от начала переходной кривой до вычисляемой точки;

l _{2 i} - расстояние от начала второй стягивающей хорды до вычисляемой точки.

Величины y_i и q_i вычисляются по формулам:

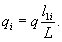
11.28. При разбивках в пределах круговой кривой принято заменять круговую линию ломаной, составленной из хорд или секущих. Длины хорд или секущих выбираются с таким расчетом, чтобы отклонения этих линий от кривой были минимальными и ими можно было бы пренебречь. В ряде случаев предпочитают пользоваться длинными хордами, чем достигается значительное уменьшение объема разбивочных работ. В этом случае необходимо вводить поправки за уклонения кривой от хорды.

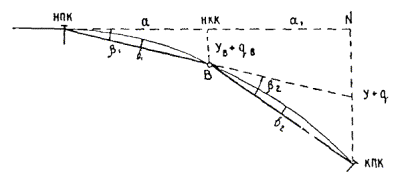
Рис. 11.14. Разбивка переходной кривой с помощью двух стягивающих хорд

11.29. При разбивке круговых кривых короткими хордами задаются допустимой величиной стрелы прогиба b в середине хорды, которой можно пренебречь. Затем определяют приближенную длину хорды s ¢ по формуле

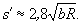
Получают величину ,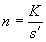

где K - полная длина кривой от КПК₁ до НПК₂. За число хорд п принимают ближайшее большее к величине n целое число. После этого подсчитывается длина дуги k_s, соответствующая принятой длине хорды, по формуле

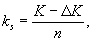
где K - длина круговой кривой по разбивочной оси, получаемая из разности пикетажа НПК₂ и КПК₁, с учетом неправильного пикета;

D K - поправка в длину круговой кривой за смещение ее с разбивочной оси на ось тоннеля, которая определяется по формуле

Необходимые для вычисления координат концов хорд длины их s вычисляют по формуле

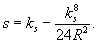
Центральный угол g, соответствующий длине хорды, вычисляется по формуле (рис. 11.15)

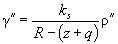
или по формуле

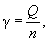
где Q - центральный угол, соответствующий полной длине круговой кривой (рис. 11.5).

Для вычисления координат концов хорд в качестве исходных служат (см. рис. 11.15) дирекционный угол линии ЦК-КПК₁ и координаты точки КПК₁ (вычисленные на оси тоннеля), а в качестве примычных - дирекционный угол линии НПК₂-ЦК и координаты точки НПК₂ (также на оси тоннеля).

Угол, составленный радиусом с первой и последней хордами, равен 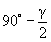. Углы поворота между хордами равны 180° - g.

11.30. При использовании длинных хорд приходится вводить поправки за стрелы прогиба круговой кривой относительно хорды. Вычисление стрел прогиба производится через 2 м по кривой, по приближенной формуле (рис. 11.16)

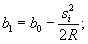
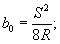
где b ₀ - стрела прогиба в середине хорды;

S - длина всей хорды;

s_i - расстояние точки i от середины хорды.

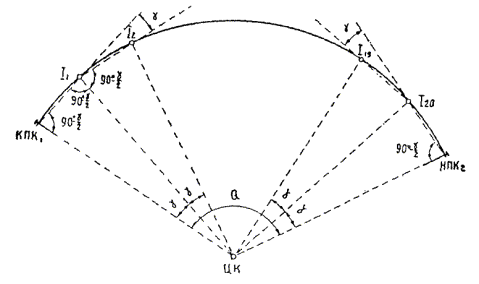
Рис. 11.15. Разбивка круговой кривой короткими хордами

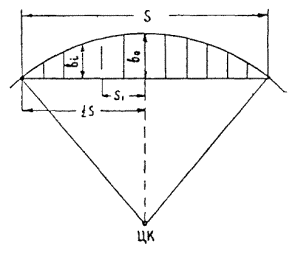
Рис. 11.16. Вычисление стрел прогибадля длинной хорды

В необходимых случаях вычисление стрелы прогиба для кривых малых радиусов можно вести по уточненной формуле

b_i = b ₀ - f_i, где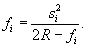

f_i вычисляется методом приближения с помощью логарифмической линейки.

Вычисление элементов и координат концов хорд производится по аналогии с вычислениями для коротких хорд. Целесообразно вычислять смещения и пикетаж полигонометрических знаков относительно концов соответствующих хорд, что облегчает задание направления в натуре.

11.31. Разбивка круговых кривых по секущим позволяет увеличить длину основной разбивочной линии. В этом случае также задаются допустимой величиной стрелы прогиба, которой можно пренебречь.

Задаваясь максимально допустимой величиной b (рис. 11.17), определяют приближенную длину секущей s ¢ по формуле

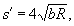
где b - максимальное отклонение секущей от круговой кривой (в середине секущей и на концах ее).

Длины крайних секущих составляют 0,85 от нормальной длины секущей, так как один из их концов лежит непосредственно на кривой. Приближенное значение п ¢ числа полных секущих определяется по формуле

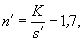
где К - полная длина кривой от КПК₁ до НПК₂

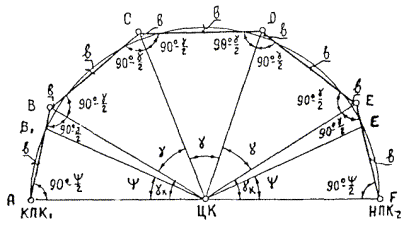
Рис. 11.17. Разбивка круговой кривой секущими

За число полных секущих п берется ближайшее большее целое число к п ¢ и определяется точная длина k_s дуги, соответствующая полной секущей, по формуле

где D K - то же, что и в п. 11.29.

Затем находится длина полной секущей по формуле

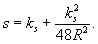
Длины неполных секущих s _н, расположенных у концов круговой кривой, и длины дуг k _н, им соответствующих, вычисляются по формулам:

s _н = 0,85 s; k _н = 0,85 k_s,

Центральный угол g, стягивающий полную секущую, определяется по формуле

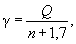
где Q - центральный угол, соответствующий полной длине круговой кривой (см. рис. 11.5).

Центральный угол g_н соответствующий неполной секущей, вычисляется по формуле

g_н = 0,85g.

Углы g и g_н могут быть вычислены также по формулам:

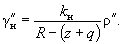
Далее вычисляется угол y (см. рис. 11.17) по формуле

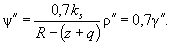
Имея все вышеперечисленные данные, производят вычисления координат концов секущих аналогично вычислению координат концов хорд. Целесообразно получать смещения и пикетаж полигонометрических знаков относительно концов соответствующих секущих.

Приложение 11-1

ПРОВЕРКА
координат пикетов прямого участка трассы

№№ точек	Дирекционные углы a	sin a	Меры линий	Приращения координат и их поправки	Координаты
°	¢	²	cos a	± D Y	± D X	Y	X
Левый путь
ПК 43								7389,063	2371,356
		22,1	0,954098	100,000	+95,4098	+29,9493
			0,299493
ПК 44								7484,473	2401,305
		22,1	0,954098	100,000	+95,4098	+29,9493
			0,299493
ПК 45								7579,883	2431,255
		22,1	0,954098	100,000	+95,4098	+29,9493
			0,299493
ПК 46								7675,292	2461,204
		22,1	0,954098	100,000	+95,4098	+29,9493
			0,299493
ПК 47								7770,702	2491,153
		22,1	0,954098	100,000	+95,4098	+29,9493
			0,299493
ПК 48								7866,112	2521,102

Приложение 11-2

ПРОВЕРКА
элементов трассы криволинейного тоннеля

№№ точек	Углы поворота (левые)	Дирекционные углы a	sin a	Меры линий	Приращения координат и их поправки	Координаты
°	¢	²	°	¢	²	cos a	± D Y	± D X	Y	X
Левый путь
ПК 47						22,1
ПК 48			00,0								7866,112	2521,102
					22,1	0,954098	46,439	+44,307	+13,908
						0,299493
НКК 3 лев.			00,0								7910,419	2535,010
ПК 48 + 46,439						22,1	0,954098	126,959	+121,131	38,023
						0,299493
УП 3 лев.			41,4								8031,550	2573,033
					03,5	0,993636	126,959	+126,151	-14,301
						0,112642
ККК 3 лев.			00,0								8157,701	2558,732
ПК 50 + 81,828
					03,5	0,993636	18,172	+18,057	-2,047
						0,112642
ПК 51			00,0								8175,758	2556,685
					03,5
ПК 52

Приложение 11-3

№№ точек	Углы поворота (левые)	Дирекционные углы a	sin a	Меры линий	Приращения координат и поправки	Координаты
°	¢	²	°	¢	²	cos a	± D Y	± D X	Y	X
Вычисление координат центра кривой «три» по левому пути
ПК 47						22,1
НКК			00,0								7910,419	2535,010
ПК 48 + 46,439
					22,1	0,299493	600,000	+179,696	-572,459
						0,954098
ЦК3 лев			41,1						+67,585	+596,182	8090,115	1962,551
					03,5	0,112642	600,000	+1	-1
						0,993636
ККК			00,0								8157,701	2558,732
ПК 30 + 81,828
					03,5	å	1200,000	+247,281	+23,723
ПК 51	å			41,4
Вычисление координат пикетов на круговой кривой по левому пути
НКК						22,1
ЦК3 лев			52,9								8090,115	1962,551
					15,0	0,213243	600,000	-127,946	+586,199
						0,976999
ПК 49											7962,169	2548,750
НКК						22,1
ЦК3 лев			51,0								8090,115	1962,551
					13,1	0,023496	600,000	-14,098	+599,834
						0,999724
ПК 50											8076,017	2552,385

Приложение 11-4

№№ точек	Углы поворота (левые)	Дирекционные углы a	sin a	Меры линий	Приращения координат и их поправки	Координаты
°	¢	²	°	¢	²	cos a	± D Y	± D X	Y	X
Вычисление координат начала первой переходной кривой (левый путь)
ПК 47						22,1
ПК 48			00,0								7866,112	2521,102
					22,1	0,954098	21,433	+20,449	+6,419
						0,299493
НПК1			00,0								7886,561	2527,521
ПК 48 + 21,433						22,1	0,954098	25,006	+23,858	+7,489
						0,299493
НКК											7910,419	2535,010
ПК 48 + 46,439							å	46,439	+44,307	+13,908
Вычисление координат конца первой переходной кривой (левый путь)
ПК 48						22,1
НПК1			00,0								7886,561	2527,521
ПК 48 + 21,433						22,1	0,954098	49,991	+47,696	+14,972
						0,299493
N 1			00,0								7934,257	2542,493
					22,1	0,299493	0,694	+0,208	-0,662
						0,954098
КПК1											7934,465	2541,831
ПК 48 + 71,433							å	50,685	+47,904	+14,310
НКК						22,1
ПК 48 + 46,439
ЦК3 лев			14,4						-1	+1	8090,115	1962,551
					36,5	0,259491	599,826	-155,649	+579,279
						0,965745
КПК1											7934,465	2541,831
ПК 48 + 71,433

Приложение 11-5

ВЫЧИСЛЕНИЕ
пикетажа и смещения знака на прямом участке трассы

№№ точек	Y	X	a	D Y cos a	-D X sin a	d	Пикетаж
D Y	D X	sin a	cos a	D Y sin a	D X cos a	D
ПК 47	7770,702	2491,153	72°34¢22²	+14,250	-13,280	+0,970
ПЗ 1721	7818,284	2505,072			+45,397	+4,169	+49,566	ПК 47 + 49,566
+47,582	+13,919	+0,954098	+0,299493

Приложение 11-6

ВЫЧИСЛЕНИЕ
пикетажа и смещения знака на участке переходной кривой

№№ точек	Y	X	a	D Y cos a	-D X sin a	d '	Пикетаж
D Y	D X	sin a	D Y sin a	D Y cos a	D X cos a	D
ПК 48	7866,12	2521,102	72°34¢22²	+16,974	-15,830	+1,144
ПЗ 1725	7922,738	2537,694			+54,075	+4,969	+59,044	ПК 48 + 59,044
+56,676	+16,592	+0,954098	+0,299493

l_i = ПК 48 + 59,044 - ПК 48 + 21,439 = 37,605;

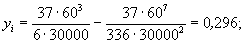
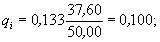
y¢_i = y_i + q_i = 0,396.

Удаление ПЗ 1725 от линии тангенса _d¢ = +1,144

y¢_i = -0,396

Удаление ПЗ относительно оси тоннеля d = +0,748

Пикетаж ПЗ 1725 = ПК 48 + 59,044.

Приложение 11-7

ВЫЧИСЛЕНИЕ
пикетажа и смещения знака на участке круговой кривой

№ точки	Y	X	tg a (a)	sin a	E
D Y	D X	a	cos a
ЦК 3	8090,115	1962,551	0,122057
ПЗ 1733	8017,357	2558,649	(6°57¢32²)	0,121158	(600,522)
-72,758	+596,098	353°02¢28²	0,992634	600,521

Вычисление смещения

Радиус разбивочной кривой R	600,000
-(z + q)	-0,307
R - (z + q)	599,693
- E	-600,521
Удаление ПЗ от оси тоннеля δ	-0,828
Вычисление пикетажа
ацк - НКК	342°34¢22²
ацк - ПЗ 1733	353 02 28
Q	+10 28 06
Q²	+37 686"
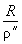
	0, 002 909
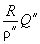
	+109,624
ПК НКК	ПК 48 + 46,439
Поправка за неправильный пикет	-
ПК ПЗ 1733	ПК 49 + 56,063

Глава 12

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: