 |
Напряжения и деформации в точке тела
|
|
|
|
Н.В. КИСЛОВ
Деформации и напряжения
В горных породах
Учебное пособие по дисциплине
«Физико-механические свойства и разрушение горных пород»
для студентов специальности 1-36.10.01 – Горные машины
и оборудование
Минск 2005
УДК 622.236.234
Кислов Н.В. Деформации и напряжения в горных породах: Учебное пособие для студ. спец. 1-36.10.01 – Горные машины и оборудование. – Мн.: БНТУ, 2005. – 54 с.
Изложены основы механики горных пород, занимающейся определением деформаций и напряжений в породах при действии внешних сил. Выполнен анализ методов оценки интенсивности деформаций как перерабатывающей способности различных исполнительных органов горного оборудования. Приводится методика оптимизации конструктивных и режимных параметров перерабатывающих устройств на стадии их проектирования.
Рецензенты:
Профессор кафедры «Горные работы» БНТУ
доктор техн. наук Н.И. Березовский
Главный научный сотрудник лаборатории
физико-химической механики ИПИПРЭ НАН РБ
доктор техн. наук Г.П. Бровка
П р е д и с л о в и е
Добыча полезных ископаемых неразрывно связана с механическим воздействием на горные породы. Для того, чтобы извлечь породу из недр необходимо вначале создать систему горных выработок. При последующей разработке полезных ископаемых также приходится иметь дело с такими механическими явлениями в горных породах как их деформация, разрушение и перемещение, которые вызываются приложенными напряжениями.
Сказанное не охватывает всех областей практики, где требуется знание механизма деформации, разрушения и движения горных пород. Изучением механических процессов, происходящих в горных породах, занимается механика горных пород (МГП), основу которой составляет механика деформируемого твердого тела (МДТТ). Математический язык МДТТ – тензорный. Сама МДТТ является частью механики сплошной среды (МСС) – обширной и разветвленной науки, изучающей макроскопические движения твердых, жидких и газообразных сред.
|
|
|
В пособии изложены основы механики горных пород (МГП), занимающейся определением деформаций и напряжений в породах при действии внешних сил. Особое внимание уделено анализу существующих методов определения интенсивности деформаций как перерабатывающей способности различных исполнительных механизмов горного оборудования.
Процесс разрушения горных пород происходит в активном деформируемом объеме. В этом случае описание напряженного и деформационного состояния породы возможно лишь с применением результатов исследований по теории упругости и пластичности, что позволило проф. Ф.А. Опейко предложить расчетный метод оценки перерабатывающей способности различных исполнительных органов горного оборудования еще на стадии разработки их конструктивных схем. В итоге представляется возможным оптимизировать конструктивные и режимные параметры оборудования исходя из заданной интенсивности деформации той или иной горной породы без предварительного создания экспериментальных образцов перерабатывающих устройств и их испытаний.
Учебное пособие «Деформации и напряжения в горных породах»: предназначено для студентов специальности 1-36.10.01 – Горные машины и оборудование, может быть полезно для аспирантов и инженерно-технических работников, занимающихся вопросами оценки перерабатывающей способности различных устройств и энергозатрат на измельчение, экскавацию, перемешивание и формование продуктов добычи полезных ископаемых и других материалов.
|
|
|
ОСНОВНЫЕ ПОНЯТИЯ
Деформация горных пород – изменение относительного положения частиц пород, вызывающее изменение размеров, объема и формы отдельностей или участков массивов горных пород.
По физической сущности деформации разделяют на упругие, исчезающие после прекращения вызвавшей их нагрузки, пластические, если после снятия нагрузки они не исчезают, и предельные (разрушающие), которые сопровождаются нарушением сплошности вследствие возникающих в горных породах новых поверхностей раздела. Длительное действие постоянных нагрузок приводит к постепенному росту деформации (ползучесть горных пород). При этом наблюдается постепенный переход упругой деформации в пластическую и далее в разрушающую. По преобладающему типу деформации все горные породы подразделяются на упругохрупкие (кварциты, граниты), упругопластические (базальты, роговики) и пластические (мраморы, гипсы).
Выделяют два простейших вида деформации – линейную и сдвиговую. Линейные деформации оцениваются показателем относительной деформации растяжения-сжатия, равным отношению приращения линейного размера образца к исходному. Сдвиговая деформация определяется величиной угла сдвига грани образца.
Знание деформации породы необходимо для определения напряжений.
Теория напряжений изучает внутренние силы в твердом теле. Эти силы выражают взаимодействие между собой молекул. Меру внутренних сил называют напряжением. При действии внешних сил в породе изменяется взаимное расположение между ее точками, что приводит к возникновению дополнительных внутренних сил. Для их обнаружения в теории напряжений используются известные из теоретической механики метод сечений и аксиома связей. Напряжения изменяются при переходе от одной частицы к другой. Поэтому в общем случае напряженное состояние тела является неоднородным, образуя поле напряжений. Вследствие этого в механике горных пород уравнения равновесия составляются для произвольной бесконечно малой частицы породы. Связь внутренних напряжений с внешними силами осуществляется с помощью граничных условий, получаемых из условий равновесия бесконечно малых частиц.
В механике горных пород молекулярная природа строения вещества не учитывается, так как ставится задача исследования наблюдаемых макроскопических процессов среды как целого. Поэтому предполагается, что вещество непрерывно заполняет выделенный объем.
|
|
|
Концепция сплошности вещества является основным постулатом механики деформируемого твердого тела и, в частности, механики горных пород. Бесконечно малый объем среды, наделенный бесконечно малой массой, называют физической частицей или материальной точкой.
Любое твердое тело в механике называют однородным, если оно имеет одинаковые свойства во всех материальных точках. Породу считают изотропной по отношению к определенному свойству, если это свойство в выбранной материальной точке одинаково по всем направлениям. В противном случае породу считают анизотропной по отношению к тем свойствам, которые зависят от напряжения.
Понятия сплошности, изотропности и неизменности объема материала положены в основу математического описания напряженно-деформированного состояния горных пород.
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТОЧКЕ ТЕЛА
Выделим мысленно в пласте или массиве породы малый элемент, имеющий форму куба, ребра которого равны соответственно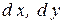 
и 
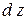(рис. 1). В результате приложения внешних сил к граням пласта или массива или действия сил, распределенных по всему объему породы, в любом произвольно выделенном малом кубе (материальной точке) возникает напряженное состояние. Оно будет характеризоваться нормальными напряжениями 
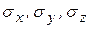и касательными напряжениями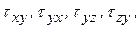 
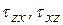, приложенными к граням куба и действующими в определенных направлениях. Эти напряжения называют соответственно компонентами нормального напряжения и компонентами касательного напряжения.
 |
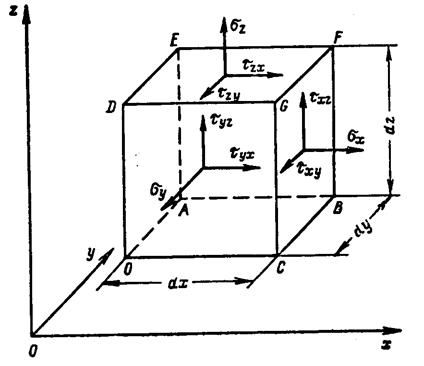Рис. 1. Выделенный из сплошной среды малый элемент в виде куба
Совокупность девяти компонент напряжений полностью характеризует напряженное состояние в малом элементе тела. Эта совокупность компонент образует тензор напряжений
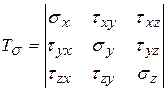. (1)
Породу в механике горных пород условно принимают однородной и изотропной. Тогда учитывая положение статики о равенстве нулю полного момента сил, действующих на малый элемент, можно записать, что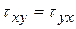 
, 
, 
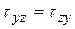. Поэтому для описания напряженного состояния тела достаточно шести компонент напряжений.
|
|
|
Подробное описание напряженного состояния в точке тела и свойств тензора напряжений имеется в трудах известных ученых Н.Е. Кочина, С.П. Тимошенко, Л.Д. Ландау и многих других.
Из теории напряжений известно, что в каждой точке нагруженного тела всегда существуют три взаимно перпендикулярных площадки, по которым действуют одни только нормальные напряжения, а касательные равны нулю. Нормальные напряжения на этих площадках называются главными, а направления соответствующих нормалей образуют главные оси тензора напряжений. Главные нормальные напряжения обозначают через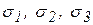 
, при этом 
. Если главные оси тензора напряжений принять за оси координат, то тензор напряжений примет вид:
. (2)
Плоскости, по которым действуют главные напряжения, также называются главными. На площадках, делящих углы между главными плоскостями пополам, действуют одни только касательные напряжения, которые называются главными и определяются по формулам
, 
, 
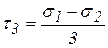. (3)
Таким образом, в каждой точке тела можно создать любое напряженное состояние, приняв главные нормальные напряжения или главные касательные направления. Однако направления главных осей выбрать сложно. Поэтому в расчетах предпочитают пользоваться закономерностью (1).
Тензор напряжений (1) можно представить в виде
, (4)
где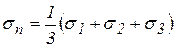 
– среднее нормальное напряжение;
– единичный тензор;
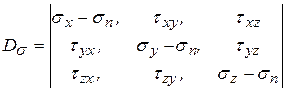– дивиатор напряжений.
Величина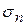 
называется средним нормальным напряжением. Оно не зависит от выбора осей координат, то есть является инвариантом. Следовательно, 
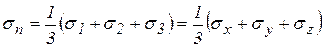. Тензор 
характеризует сдвиг. Его называют дивиатором напряжений.
Введем новые обозначения для напряжений. Пусть 
, 
, 
, 
, 
, 
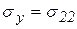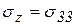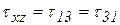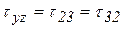. Тогда тензор и дивиатор напряжений примут вид:
, 
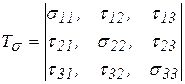. (5)
Приложение напряжения к элементарному объему тела вызывает его деформацию. Рассмотрим и в этом случае элементарный объем тела в виде куба. Действующие на куб напряжения вызывают смещение его граней и искажение. Деформация в каждой точке тела разлагается на всестороннее сжатие (или растяжение) и сдвиг. В этом случае компонентами тензора деформаций будут шесть величин, характеризующих деформации растяжения (сжатия) и деформации сдвига,
, (6)
где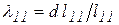 
, 
, 
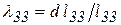– относительные изменения длины ребер выделенного объема породы по направлению осей системы координат (рис. 2, а); 
,
, 
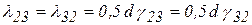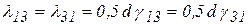– половины углов сдвига вокруг осей 
, 
и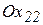 
соответственно (рис. 2, б).
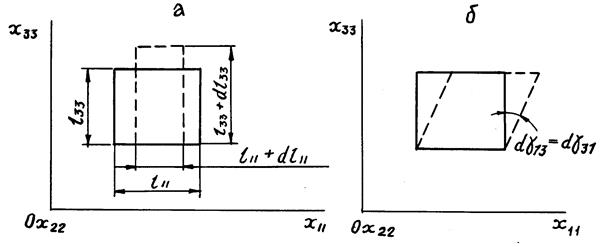
Рис. 2. Деформация выделенного из сплошной среды куба:
|
|
|
а – растяжение-сжатие вдоль осе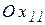й 
и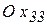 
;
б – сдвиг вокруг оси 
По аналогии с дивиатором напряжений дивиатор деформаций имеет вид:
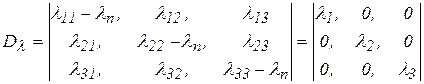. (7)
Ранее отмечалось, что при деформировании породы соблюдается условие неизменности объема, то есть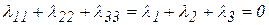 
. В общем случае 
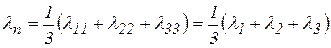, где 
– главные деформации.
Оценка величин дивиаторов напряжений и деформаций необходима для определения работы формоизменения, отнесенной к единице объема породы при ее разрушении, переработке и перемещении. Эта удельная работа в настоящее время оценивается полупроизведением дивиаторов напряжений и деформаций
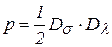. (8)
Процессы разрушения горных пород происходят в активном деформируемом объеме за пределами упругих деформаций, то есть после перехода из равновесного состояния в пластическое или вязко-пластическое. При этом затраты мощности на деформирование (разрушение) горной породы определяются как произведение удельной работы формоизменения на секундную производительность исполнительного органа горной машины.
|
|
|
