Интенсивность деформаций породы

ПРИ ФРЕЗЕРОВАНИИ

 

Определение интенсивности деформаций породы при ее фрезеровании выполним по формуле, полученной для ленточного растирателя. При фрезеровании горной породы цилиндрической фрезой в качестве подвижной ленты примем поверхность соприкосновения рабочих элементов фрезы с породой, а в качестве неподвижной – фрезеруемую поверхность массива. Переработка породы осуществляется также и при ее измельчении. Тогда формула (19) для фрезы примет вид:

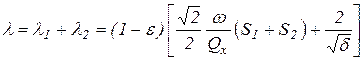, (20)

где – угловая скорость фрезы, с^-1;

– производительность фрезы по ходу машины, м³/с;

– ширина захвата фрезы, м;

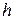– глубина фрезерования, м;

– поступательная скорость фрезы, м/с;

– статический момент площади поверхности

соприкосновения резцов с породой относительно

оси вращения фрезы, м³;

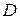– диаметр фрезы, м;

– средняя по глубине фрезерования толщина резца, м;

– суммарное число резцов фрезы;

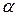– центральный угол дуги касания фрезы с породой, град;

– статический момент площади поверхности

соприкосновения экскавируемой резцами породы

с массивом, м³;

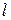– длина фигуры волочения (длина стружки), м;

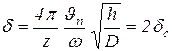– наибольшая толщина стружки при послойном

фрезеровании породы в случае , м;

– средняя толщина стружки, м.

– число резцов в полости резания.

Известно, что для устойчивой работы фрезы должно соблюдаться условие , где – производительность по фрезе, м³/с. Исходя из равенства 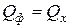длина тела волочения . После преобразований формула (20) принимает вид:

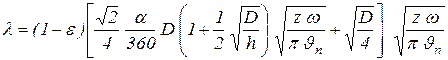. (21)

Фреза представляет собой разновидность дробилки, интенсивность деформации породы в которой на основании формулы (19) определится в общем случае следующим образом:

, (22)

где – статический момент площади соприкосновения породы с

ротором относительно его оси;

– расстояние элементарных площадок соприкосновения ротора

с породой от оси ротора.

 

ИНТЕНСИВНОСТЬ ДЕФОРМАЦИЙ ПОРОДЫ

В ШНЕКЕ

 

Напорные шнеки нашли широкое применение для обеспечения интенсивной переработки различных материалов. Практически с помощью шнека можно обеспечить любую заданную интенсивность деформаций породы.

Проф. Ф.А. Опейко рекомендует для шнека следующую формулу:

, (23)

где – статический момент площади внутренней

поверхности кожуха шнека относительно его оси;

– то же площади меридиального сечения винта шнека

относительно его оси;

– то же площади меридиального сечения породы в шнеке

относительно его оси.

В связи с тем, что отношение мало, вторым слагаемым в формуле (23) можно пренебречь. Тогда для шнека

. (24)

Определим производительность 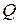однозаходного напорного шнека. Рассмотрим его меридиальное сечение (рис. 4).

 

Рис. 4. Схема меридиального сечения шнека

 

 

Выделим в меридиальном сечении одного витка шнека слой материала толщиной 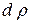на расстоянии от оси вращения. Тогда элементарная производительность через выбранное сечение

,

где – скорость породы через элементарное сечение ;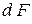

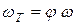– угловая скорость породы относительно оси шнека;

– угловая скорость винта шнека;

– коэффициент, учитывающий наличие вращения породы

вместе со шнеком;

– шаг шнека.

Коэффициент 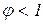и зависит от противодавления. При достаточном противодавлении, которое создается кожухом, мундштуками и другими устройствами, пространство между витками всегда полностью заполнено материалом. Для нагнетательных шнеков = 0,2-0,3; для винтовых фрез 0,5. Наибольшее расчетное значение составляет 0,77.

Полная производительность шнека

, (25)

где – статический момент площади витка породы в меридиальном

сечении шнека относительно его оси.

Найдем

,

где – радиус внутренней поверхности кожуха шнека;

– радиус вала шнека.

Установлено, что шнек развивает наибольший напор, когда соблюдается соотношение

.

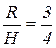Тогда производительность шнека

. (26)

Подставив выражения для и 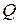в формулу (24), окончательно получим

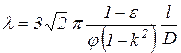. (27)

Таким образом, на величину интенсивности деформаций породы при переработке ее шнеком влияют его длина 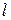и диаметр 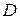. При этом должно соблюдаться условие, что .

Известны и другие способы выражения производительности шнека. Формула (26) была получена из условия, что материал перемещается в направлении, перпендикулярном меридиальному сечению витка шнека.

Рассмотрим теперь движение породы через сечение шнека, перпендикулярное его оси. Если при этом материал перемещается относительно вращающегося винта шнека, то производительность

, (28)

где – объем породы в одном витке шнека;

– площадь поперечного сечения породы в шнеке;

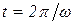– время перемещения витка на один шаг.

Выразим шаг через угол подъема наружной винтовой линии шнека

.

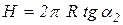Подставив выражения для и в формулу (28), после преобразования получим

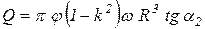. (29)

Приравняв правые части выражений (26) и (29), находим, что оптимальный, с точки зрения наибольшего развиваемого давления, угол подъема наружной винтовой линии шнека .

Если рассматривать движение породы относительно неподвижного кожуха шнека, то его производительность

, (30)

где – шаг винтовой линии, описываемой частицами

породы на внутренней поверхности кожуха шнека;

– угол подъема этой винтовой линии.

С учетом выражений для и формула (29) принимает вид

. (31)

Из формул (28)-(31) имеем

; . (32)

Формулы (25) и (28) позволяют определить площадь поперечного сечения материала в плоскости, перпендикулярной его оси, если шнек имеет произвольный профиль,

.

В общем случае , тогда .

Формула (27) может быть использована для определения размеров шнекового перерабатывающего устройства по заданной интенсивности деформаций материала.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: