 |
Последовательность расчета размеров
|
|
|
|
Перерабатывающего шнека
Для определения основных размеров однозаходного шнека, предназначенного для механической переработки горных пород, необходимы следующие исходные данные:
1. Заданная производительность 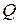 , м3/с.
, м3/с.
2. Требуемая интенсивность деформации горной породы 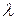 .
.
3. Коэффициент запаса интенсивности деформаций  .
.
4. Среднее тангенциальное напряжение сдвига слоев перерабатываемой породы  , Па.
, Па.
5. Поправочный коэффициент  .
.
6. Отношение 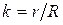 , где
, где  – радиус вала винта шнека;
– радиус вала винта шнека;
 – внутренний радиус кожуха шнека.
– внутренний радиус кожуха шнека.
7. Число заходов шнека  .
.
8. КПД привода шнека  .
.
9. Коэффициент проскальзывания  .
.
Расчетом устанавливаются основные размеры шнека и мощность, необходимая для его работы.
Последовательность расчета.
1. Из формулы (27) находят отношение длины 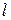 рабочей части шнека к его диаметру
рабочей части шнека к его диаметру 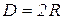 .
.
 . (66)
. (66)
2. Определяют число 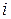 витков шнека. Так как
витков шнека. Так как  , а наибольшее давление, развиваемое шнеком, будет, если
, а наибольшее давление, развиваемое шнеком, будет, если  , то
, то
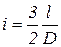 . (67)
. (67)
Основываясь на зависимости (26) для производительности шнека, вычисляют произведение 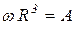
 . (68)
. (68)
4. Получаются два уравнения (67)и (68) с тремя неизвестными 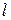 ,
, 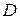 и
и  . Если по конструктивным соображениям можно принять длину
. Если по конструктивным соображениям можно принять длину 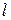 шнека, то его наружный радиус вычисляется по формуле (67)
шнека, то его наружный радиус вычисляется по формуле (67)
 . (69)
. (69)
5. Угловая скорость винта шнека согласно (68)
 . (70)
. (70)
6. Шаг шнека на основании (64)
 . (71)
. (71)
7. В соответствии с (65) наибольшее давление, развиваемое однозаходным напорным шнеком,
 . (72)
. (72)
8. Удельную затрату энергии на переработку горной породы определяют по формуле (49)
 .
.
9. Мощность, потребляемая шнеком при переработке горной породы, вычисляется по формуле (59) с учетом КПД привода
 , кВт, (73)
, кВт, (73)
где  – статический момент площади внутренней поверхности
– статический момент площади внутренней поверхности
кожуха шнека относительно его оси, м3.
|
|
|
Возможны другие варианты расчета перерабатывающего шнека в зависимости от того, какие заданы исходные данные. Например, если заданы 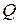 ,
, 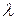 ,
,  и
и  , то расчетом определяются
, то расчетом определяются  ,
,  ,
, 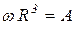 ,
,  ,
,  ,
, 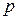 и
и  . Для переработки пород применяются и многозаходные шнеки. В этом случае при определении произведения
. Для переработки пород применяются и многозаходные шнеки. В этом случае при определении произведения  в формулу (26) для производительности
в формулу (26) для производительности 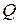 вводится сомножителем число заходов
вводится сомножителем число заходов  винта шнека. Длина шнека должна быть ограничена. Тогда ее находят по принятому диаметру шнека и вычисленному числу
винта шнека. Длина шнека должна быть ограничена. Тогда ее находят по принятому диаметру шнека и вычисленному числу 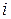 витков шнека.
витков шнека.
Пример расчета перерабатывающего шнека
В результате расчетов определению подлежат: конструктивные и кинематические параметры шнека; наибольшее давление, развиваемое шнеком; предельная и полезная мощности, затрачиваемые на работу шнека; коэффициент полезного действия (КПД) шнека; давление, интенсивность деформаций породы и КПД для выбранных длины и диаметра шнека при переменном шаге витков в случае:
а) постоянной угловой скорости шнека;
б) постоянной производительности.
По результатам расчетов необходимо построить графические зависимости давления, интенсивности деформаций и КПД от отношения шага витков к радиусу шнека. Установить влияние этого отношения на производительность при постоянной угловой скорости (вариант А) и на угловую скорость при постоянной производительности (вариант Б). Бланк задания и исходные данные для расчетов приведены в приложении.
Таблица 1
Исходные данные
| №№ | Наименование | Обозначение | Ед. изм. | Значение |
| 1. | Интенсивность деформаций | 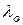
| ||
| 2. | Коэффициент запаса интенсивности деформаций | 
| 1,1 | |
| 3. | Коэффициент, учитывающий вращение породы с винтом шнека | 
| 0,2 | |
| 4. | Отношение радиусов винта шнека | 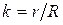
| 0,5 | |
| 5. | Число заходов шнека | 
| ||
| 6. | Коэффициент проскальзывания | 
| 0,2 | |
| 7. | Производительность | 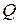
| м3/с | 0,025 |
| 8. | Тангенциальное напряжение | 
| Па | |
| 9. | КПД привода шнека | 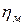
| 0,8 |
Расчет шнека
|
|
|
1. Расчетная интенсивность деформации горной породы
 .
.
Принимаем 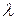 = 350.
= 350.
2. Отношение длины 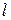 шнека к его диаметру
шнека к его диаметру 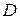
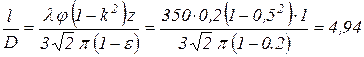 .
.
3. Число витков шнека
 .
.
Принимаем 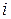 = 8. Тогда расчетное отношение
= 8. Тогда расчетное отношение  будет
будет
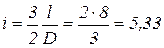 .
.
4. Пусть длина шнека 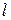 = 2 м. Тогда радиус шнека
= 2 м. Тогда радиус шнека
 м.
м.
Диаметр шнека  м.
м.
Диаметр кожуха шнека принимается в соответствии со стандартом на цельнотянутые трубы и в случае необходимости уточняется радиус шнека.
5. Параметр производительности
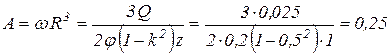 м3/с.
м3/с.
6. Шаг витков шнека
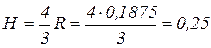 м.
м.
7. Угловая скорость шнека
 1/с.
1/с.
8. Частота вращения шнека
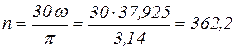 об/мин.
об/мин.
9. Действительная интенсивность деформаций породы
 ,
,
где  – статический момент площади внутренней поверхности
– статический момент площади внутренней поверхности
кожуха шнека относительно его оси, м3.
10. Наибольшее давление, развиваемое шнеком,
 Па = 201 кПа.
Па = 201 кПа.
11. Удельная затрата энергии при переработке горной породы (предельная)
 Па = 2144 кПа.
Па = 2144 кПа.
12. Предельная мощность для переработки горной породы
 кВт.
кВт.
13. Полезная мощность при наибольшем давлении
 кВт.
кВт.
14. Коэффициент полезного действия перерабатывающего шнека как винтового насоса
 .
.
Вычисленные конструктивные и кинематические параметры являются оптимальными, так как в рассмотренном случае  .
.
Вариант А. Расчет для 
15. Пусть  2 м = const,
2 м = const, 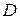 = 0,375 м = const, а Н меняется с шагом
= 0,375 м = const, а Н меняется с шагом  = 0,25 - 0,1875 = 0,0625 м в большую и меньшую стороны от оптимального значения Н = 0,25 м, при котором давление
= 0,25 - 0,1875 = 0,0625 м в большую и меньшую стороны от оптимального значения Н = 0,25 м, при котором давление  наибольшее. Тогда расчетные значения шага витков шнека будут:
наибольшее. Тогда расчетные значения шага витков шнека будут:
 и
и  .
.
Расчеты по этим формулам после ранжирования дают следующие значения шага  витков шнека, сведенные в табл. 2.
витков шнека, сведенные в табл. 2.
16. Давления, развиваемые шнеком при разных значениях шага витков, определяются по формуле
 .
.
Расчеты выполнены при условии, что  . Полученные результаты сведены в табл. 2.
. Полученные результаты сведены в табл. 2.
17. Производительность шнека при заданных значениях шага витков
 .
.
Для расчетных значений  полученные производительности представлены в табл. 2.
полученные производительности представлены в табл. 2.
18. Интенсивность деформации горной породы при заданных значениях шага витков шнека  изменяется в пределах 190-504 единиц (табл. 2).
изменяется в пределах 190-504 единиц (табл. 2).
19. Численные значения удельной затраты энергии (предельной) при переработке породы шнеком для разных величин шага витков, вычисленные по формуле  , сведены в табл. 2.
, сведены в табл. 2.
20. Предельная мощность для переработки породы при различных значениях 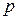 и
и 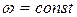 в соответствии с формулой
в соответствии с формулой
|
|
|

остается постоянной и составляет 67 кВт.
21. Полезная мощность  с увеличением шага
с увеличением шага  и
и 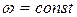 возрастает(табл. 2).
возрастает(табл. 2).
22. Коэффициент полезного действия шнека как винтового насоса  возрастает по мере увеличения шага витков (табл. 2).
возрастает по мере увеличения шага витков (табл. 2).
23. Полученные данные (табл. 2) служат основой для построения графических зависимостей производительности, интенсивности деформаций, давления и КПД шнека от его конструктивного параметра 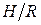 (рис. 10).
(рис. 10).
Таблица 2
Расчетные данные для шнека с 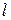 = 2 м и
= 2 м и 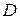 = 0,375 м
= 0,375 м
при  = 37,926 с-1 (
= 37,926 с-1 (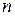 = 362,2 об/мин)
= 362,2 об/мин)
| № |  ,
м ,
м
|  ,
м ,
м
| 
|  ,
кПа ,
кПа
| 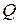 ,
м3/с ,
м3/с
| 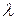
| 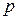 ,
кПа ,
кПа
|  ,
кВт ,
кВт
|  ,
кВт ,
кВт
| 
|
| 0,1875 | 0,1875 | 1,00 | 178,7 | 0,0188 | 4,20 | 0,063 | ||||
| 0,2500 | 1,33 | 201,1 | 0,0250 | 6,28 | 0,094 | |||||
| 0,3125 | 1,67 | 193,4 | 0,0312 | 7,54 | 0,112 | |||||
| 0,3750 | 2,00 | 178,7 | 0,0375 | 8,38 | 0,125 | |||||
| 0,4375 | 2,33 | 164,1 | 0,0438 | 8,98 | 0,134 | |||||
| 0,5000 | 2,67 | 150,8 | 0,0500 | 9,42 | 0,140 |
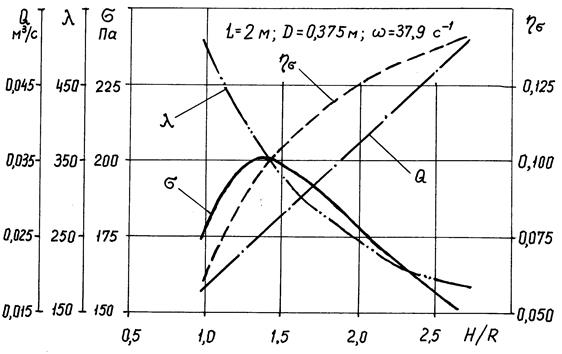 |
Рис. 10. Зависимости производительности 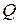 , интенсивности
, интенсивности
деформаций 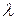 , давления
, давления  и КПД
и КПД  шнека от
шнека от
его конструктивного параметра 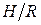
Вариант Б. Расчет для  .
.
24. Принимаем производительность постоянной. В соответствии с исходными данными 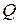 = 0,025 м3/с. Тогда угловая скорость шнека для разных значений его шага может быть вычислена по формуле
= 0,025 м3/с. Тогда угловая скорость шнека для разных значений его шага может быть вычислена по формуле
 .
.
Полученные значения  и все последующие результаты расчетов сведены в табл. 3 и использованы для построения графиков (рис. 11).
и все последующие результаты расчетов сведены в табл. 3 и использованы для построения графиков (рис. 11).
Таблица 2
Расчетные данные для шнека с 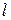 = 2 м и
= 2 м и 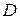 = 0,375 м
= 0,375 м
при 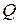 = 0,025 м3/с
= 0,025 м3/с
| № |  ,
м ,
м
|  ,
м ,
м
| 
|  ,
1/с ,
1/с
|  ,
кПа ,
кПа
| 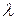
| 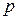 ,
кПа ,
кПа
|  ,
кВт ,
кВт
|  ,
кВт ,
кВт
| 
|
| 0,1875 | 0,1875 | 1,00 | 50,60 | 178,7 | 89,1 | 5,58 | 0,063 | |||
| 0,2500 | 1,33 | 37,93 | 201,1 | 67,0 | 6,28 | 0,094 | ||||
| 0,3125 | 1,67 | 30,34 | 193,4 | 53,8 | 6,04 | 0,112 | ||||
| 0,3750 | 2,00 | 25,28 | 178,7 | 44,7 | 5,58 | 0,125 | ||||
| 0,4375 | 2,33 | 21,67 | 164,1 | 38,2 | 5,13 | 0,134 | ||||
| 0,5000 | 2,67 | 19,00 | 150,8 | 33,6 | 4,71 | 0,140 |
 |
Рис. 11. Зависимости угловой скорости  , интенсивности
, интенсивности
деформаций 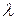 , давления
, давления  и КПД
и КПД  шнека от
шнека от
его конструктивного параметра 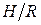
25. Интенсивность деформаций при 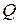 = 0,025 м3/с и
= 0,025 м3/с и  , вычисленная по формуле
, вычисленная по формуле
|
|
|
 ,
,
соответствует данным, полученным при 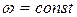 .
.
26. Удельная затрата энергии (предельная) при переработки породы шнеком для  ,
,  и
и  также соответствует значениям
также соответствует значениям 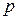 для
для  .
.
27. Предельная мощность для переработки при  , вычисленная по формуле
, вычисленная по формуле  по мере возрастания
по мере возрастания  уменьшается.
уменьшается.
28. Полезная мощность  при
при  имеет максимум в случае оптимального значения
имеет максимум в случае оптимального значения  .
.
29. КПД шнекового пресса  как винтового насоса с увеличением
как винтового насоса с увеличением 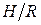 возрастает, если
возрастает, если  . Коэффициенты
. Коэффициенты  в случае
в случае  получились такими же, как и для
получились такими же, как и для  , хотя предельная и полезная мощности разнятся. Так, если при
, хотя предельная и полезная мощности разнятся. Так, если при 
 , а
, а  по мере увеличения
по мере увеличения 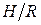 возрастает, то в случае
возрастает, то в случае 
 уменьшается, а
уменьшается, а  имеет максимум.
имеет максимум.
Приложение 1
Учреждение образования
|
|
|


