 |
Интенсивность деформаций и напряжений
|
|
|
|
Теория деформаций, изложенная в тензорном исчислении, широко используется в теории упругости и пластичности. Поэтому вполне естественно применить ее положение в расчетах, связанных с разрушением, измельчением, перемешиванием и транспортированием горных пород.
В теории упругости и пластичности для оценки интенсивности деформаций служат инварианты тензора деформаций (6). Проф. Ф.А. Опейко предложил оценивать интенсивность деформаций по обобщенной деформации на основании рассмотрения симметричного тензора второго ранга. Главные значения 
, 
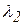и 
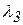тензора (6) устанавливаются из уравнения 3-й степени как его корни:
, (9)
где 
, 
, 
– инварианты тензора деформаций;
; 
; 
.
Условие неразрывности эквивалентно обращению в ноль первого инварианта тензора, то есть
.
Поэтому по Ф.А. Опейко интенсивность деформаций (обобщенная деформация) состоит из первых двух инвариантов:
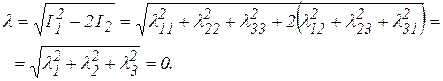(10)
Таким образом, интенсивность деформаций породы, не меняющей свой объем, характеризуется корнем квадратным из суммы квадратов главных деформаций. Эта интенсивность деформаций может быть выражена также и через любые другие составляющие тензора деформаций. Например, через деформации рястяжения-сжатия 
, 
и 
в направлении осей произвольно расположенной декартовой системы координат и половин углов сдвигов вокруг осей этой системы координат. Это позволяет избежать решения уравнения (9) и определения главных деформаций.
Для изотропного однородного тела при соблюдении условия неразрывности (неизменности выделенного объема) тензоры напряжений и деформаций совпадают. Поэтому в рассматриваемом случае интенсивность напряжений (обобщенное напряжение) можно представить следующим образом:
|
|
|
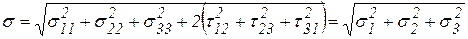, (11)
где 
и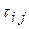 
– нормальные и тангенциальные напряжения соответственно по направлениям и вокруг осей произвольно выбранной системы координат 
; 
, 
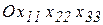и 
– главные напряжения.
ИНТЕНСИВНОСТЬ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
ПРИ ЧИСТОМ СДВИГЕ
Подавляющее большинство экскавирующих, перерабатывающих, формующих и транспортирующих механизмов и устройств при разработке и обогащении полезных ископаемых работают таким образом, что с помощью их обеспечивается чистый сдвиг, то есть порода деформируется только вокруг одной из осей выбранной системы координат. Зависимость (10) для чистого сдвига (рис. 2.1, б) принимает вид
, (12)
так как в этом случае 
. Причем для изотропного однородного тела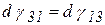 
.
Аналогично для интенсивности напряжений при чистом сдвиге согласно формуле (11) имеем
. (13)
Таким образом, в случае чистого сдвига при упруго-пластических деформациях без изменения объема интенсивности деформаций и напряжений выражаются через соответствующие составляющие тензора одинаково с одним и тем же множителем 
. Это обстоятельство следует считать важным, так как напряжения и деформации сдвига играют значительно бóльшую роль при расчетах перерабатывающих устройств, чем нормальные напряжения и деформации.
В теории упругости и пластичности интенсивность деформаций и напряжений при чистом сдвиге оценивается соответственно зависимостями 
и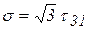 
. Сравнивая коэффициенты при соответствующих компонентах тензоров напряжений и деформаций, можно заключить, что формулы (12) и (13) имеют более простой вид для чистого сдвига (оба коэффициента равны ).
ИНТЕНСИВНОСТЬ ДЕФОРМАЦИЙ В
ЛЕНТОЧНОМ РАСТИРАТЕЛЕ
Ленточные растиратели в настоящее время имеют весьма ограниченное применение. Однако их работа представляет интерес с теоретической точки зрения, так как здесь наиболее наглядно проявляется чистый сдвиг.
|
|
|
Ленточный растиратель (рис. 3) состоит из двух подвижных лент, расположенных друг относительно друга таким образом, чтобы в пространство между ними мог поступать перерабатываемый материал. Верхняя лента перемещается со скоростью 
, превышающей скорость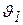 
нижней ленты. Поэтому в пространстве между лентами имеет место чистый сдвиг вокруг оси 
. Следовательно, для определения интенсивности деформации породы в ленточном растирателе можно воспользоваться формулой (12). Естественно, что перерабатывающая способность ленточного растирателя будет зависеть от его конструктивных и режимных параметров, т.е. от зазора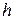 
между лентами, их рабочей ширины 
и длины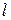 
, соотношения между скоростями и 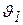лент, а также от проскальзывания материала по рабочим поверхностям ленточного растирателя.
 |
Рис. 3. Схема ленточного растирателя
Суммарный угол 
сдвига слоев породы за время 
ее пребывания в рабочем пространстве растирателя (проскальзывание породы относительно лент не учитываем)
, (14)
где 
– угловая скорость сдвига.
Время пребывания породы в рабочем пространстве растирателя 
, где 
– средняя скорость материала в пространстве между лентами. При заданной производительности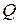 
средняя скорость 
. Тогда время
. (15)
Подставив равенства для и в формулу (12), получим
. (16)
В общем случае производительность
.
Тогда интенсивность деформаций материала в ленточном растирателе
. (17)
Формулу (16) можно также преобразовать следующим образом:
, (18)
где 
– статический момент площади 
поверхности соприкосновения с породой верхней ленты растирателя относительно нижней ленты.
При проскальзывании верхней ленты относительно породы ее интенсивность деформаций уменьшается. Скольжение возникает из-за того, что предельное напряжение сдвига внутри породы больше внешнего предельного напряжения сдвига. Причем материал отстает от верхней ленты и опережает нижнюю ленту, так как 
. Пусть скорость проскальзывания будет 
. Тогда коэффициент скольжения
.
Эта формула показывает, что при определенных свойствах горной породы с увеличением разности скоростей лент коэффициент скольжения уменьшается.
В случае наличия опорных роликов зазор между лентами может меняться. Изменение величины зазора 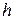по мере перемещения породы в рабочем пространстве растирателя приводит к появлению составляющих 
и 
, но они настолько малы по сравнению с 
, что ими можно пренебречь.
|
|
|
Окончательно интенсивность деформаций породы в ленточном растирателе (при чистом сдвиге)
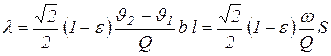. (19)
Проф. Ф.А. Опейко показал, что средняя по элементарному объему интенсивность деформаций горной породы не зависит от закона распределения скорости по поперечному сечению ее слоя. Аналогичный вывод можно сделать из анализа формулы (19). При заданной производительности 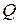величина зазора 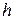и закон распределения скорости по поперечному сечению потока не оказывают влияния на величину средней по объему интенсивности деформаций при переработке породы в ленточном растирателе. Поэтому, меняя 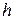, всегда можно обеспечить требуемую 
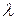при заданной .
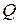Формула (19) положена проф. Ф.А. Опейко в основу расчетных зависимостей для оценки интенсивности деформаций при переработке породы в различных устройствах.
|
|
|
