Перерабатывающих устройств

 

При переработке горных пород энергия расходуется на их деформирование и на бесполезное проскальзывание относительно неподвижных и вращающихся поверхностей перерабатывающего устройства. Тогда в общем случае мощность, затрачиваемая непосредственно на механическую переработку породы,

, кВт, (51)

гд 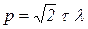– удельная затрата энергии на переработку, Па;

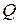– производительность перерабатывающего устройства, м³/с.

Мощность на проскальзывание породы в перерабатывающем устройстве

, кВт, (52)

где 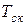– усилие, возникающее при проскальзывании породы, Н;

– скорость скольжения, м/с.

Суммарные затраты мощности при переработке горных пород

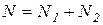. (53)

Определим мощность, необходимую для переработки горной породы в ленточном растирателе. Согласно формуле (51) с учетом того, что интенсивность деформаций породы определяется в соответствии с (19), имеем

. (53)

Горная порода в ленточном растирателе проскальзывает относительно верхней и нижней лент. Поэтому усилие скольжения . Если скорости скольжения породы у верхней и нижней ленты одинаковые и отличаются только знаком, то коэффициент скольжения 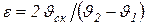. Тогда скорость скольжения

.

Подставив выражения для 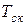и в формулу (52), получим

. (54)

Окончательно суммарные затраты мощности на переработку горной породы в ленточном расстирателе

, кВт. (55)

Из анализа этой зависимости вытекает, что мощность, потребляемая при переработке породы, не зависит от коэффициента скольжения , а следовательно, и от скорости скольжения. Вместе с тем, при увеличении уменьшается интенсивность деформаций 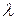. Разделив на , получим коэффициент полезного действия растирателя как перерабатывающего устройства

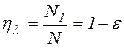. (56)

Таким образом, КПД переработки уменьшается при увеличении скорости скольжения материала относительно рабочих поверхностей перерабатывающего устройства. При этом потребляемая мощность не зависит от величины . Поэтому в расчетах затрат мощности на работу различных перерабатывающих устройств, следует пользоваться формулой

, кВт, (57)

в которой интенсивность деформаций 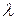вычисляется по приведенным ранее формулам без учета скольжения, т.е. сомножитель исключается. Руководствуясь этим выводом, определим мощность, необходимую для работы шнека или другого перерабатывающего устройства, имеющего ротор. В этом случае интенсивность деформаций без учета скольжения согласно формуле (18)

, (58)

где – статический момент площади внутренней поверхности кожуха

шнека или площади поверхности рабочих поверхностей дробилки

с ротором относительно оси вращения, м³;

– угловая скорость винта шнека или ротора, с^-1;

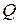– производительность, м³/с.

Подставив зависимость (58) в формулу (57), получим

, кВт. (59)

Определим мощность, потребляемую при формовании переработанной горной породы в цилиндрическом мундштуке. Ранее было показано, что для цилиндрической насадки без учета скольжения 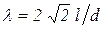. При этом производительность . Тогда согласно (57) затраты мощности

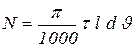. (60)

Аналогичным образом могут быть получены формулы для определения мощности, затрачиваемой на формование горных пород в других устройствах.

Для расчета формующих устройств необходимо знать возникающее в них противодавление. Рассмотрим определение противодавления на примере цилиндрического мундштука (рис. 9).

 

Рис. 9. К определению давления в цилиндрическом мундштуке

 

 

Пусть – нормальное давление в сечении мундштука, а – тангенциальное напряжение на его внутренней поверхности. Тогда для состояния равновесия

.

Отсюда

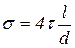. (61)

Известно, что для цилиндрического мундштука 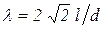. Подставив это выражение для 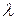в формулу (49), получим, что удельная затрата энергии на переработку горной породы

. (62)

Следовательно, противодавление в мундштуке равно по величине удельной затрате энергии 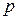на переработку породы. Последнее справедливо для формующих мундштуков любой формы.

Противодавление в формующих устройствах преодолевается за счет давления, развиваемого нагнетающими устройствами. Определим наибольшее давление, которое развивается однозаходным перерабатывающим шнеком. Согласно формуле проф. Ф.А. Опейко давление, развиваемое шнеком,

, Па, (63)

где 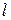– длина шнека, м;

– шаг витков шнека, м;

– число витков шнека;

– наружный радиус шнека, м;

– тангенциальное напряжение на внутренней поверхности

кожуха шнека, Па.

Для того, чтобы шнек развивал при заданной длине наибольшее давление, необходимо установить оптимальное соотношение между его размерами и . Определим это соотношение из условия . Производная

.

Приравняв ее нулю, получим

. (64)

Соотношение (64) действительно имеет максимум при , так как . Тогда наибольшее давление, развиваемое перерабатывающим шнеком,

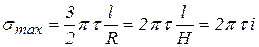. (65)

 

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: