Надежность систем с облегченным резервом

 

Как отмечалось в предыдущих лекциях, ненагруженный резерв более эффективен, чем нагруженный, и количественно показатели эффективности зависят от законов распределения наработки до отказа отдельных элементов резервированной системы.

Основным моментом, который может сказаться на оценке надежности является то, что предположение = const является довольно условным, поскольку, особенно при отсутствии технического обслуживания, очередной работающий элемент эксплуатируется до полного износа (физически должна возрастать). Поэтому принятое экспоненциальное распределение наработки элементов, переходящих из резервных в рабочие, использовалось только с целью упрощения расчетов.

Ненагруженный резерв в рамках принятых допущений не всегда осуществим. Например, в авиа- и судовых системах как основные, так и резервные элементы подвержены вибрации, ударам, повторно-статическим нагрузкам, перепадам температур и т. п. Поэтому не включенные в работу резервные элементы будут иметь некоторую 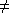0, то есть они также изнашиваются, но менее интенсивно.

Поэтому, в ряде практических случаев, уместно применять облегченный резерв:

(подключение резервных элементов (РЭ) к цепям питания для прогрева и удержания требуемых значений параметров;

(внешние нагрузки и воздействия, приводящие к изменению свойств материалов, рабочих параметров и т. п.

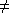При этом, РЭ будут иметь некоторую интенсивность отказов _р 0.

Рассмотрим систему, состоящую из равнонадежных основного (ОЭ) и резервного (РЭ) элементов. Элементы невосстанавливаемые.

События, обеспечивающие безотказную работу (БР) системы за наработку (0, t):

A = {БР системы за наработку (0, t)};

A₁ = {БР ОЭ за наработку (0, t)};

A₂ = {отказ ОЭ в момент < t, включение РЭ и БР его на интервале (t - )}.

Событие A представляет сумму событий A₁ и A₂

 

A = A₁ A₂

 

 

 

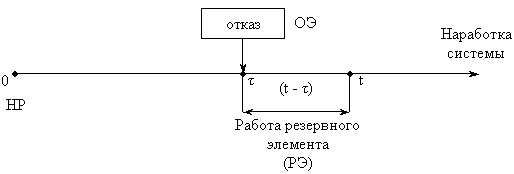
ВБР системы за наработку (0, t), т.е. к наработке t равна сумме вероятностей событий A₁ и A₂:

 

P(A) = P(A₁ ) + P(A₂),

 

где P(A) = P_с(t) – ВБР системы к наработке t;

P(A) = P₀ (t) – ВБР ОЭ к наработке t (за интервал (0, t));

P(A) = P_р (t) – ВБР РЭ к наработке t, при условии, что ОЭ отказал.

При известном законе распределения наработки ОЭ вычисление P₀ (t) не составляет труда, подробнее рассмотрено определение Pр (t).

Для этого событие A₂ раскладывается на составляющие:

A₂₁ = {отказ ОЭ при наработке < t };

A₂₂ = {БР РЭ до наработки – момент включения его в работу};

A₂₃ = {БР РЭ от до t, т.е. за интервал (t - )}.

Очевидно, событие A₂ выполнится при одновременном выполнении всех событий:

 

A₂ = A₂₁ A₂₂ A₂₃;

 

События A₂₁, A₂₂, A₂₃ являются зависимыми, но поскольку они представляют ВБР или ВО элементов, наработки до отказа которых описываются своими законами распределения, то вероятность события A₂ равна произведению вероятностей событий:

 

P(A₂ ) = P(A₂₁ ) · P(A₂₂ ) · P(A₂₃).

 

Соответствующие вероятности определяются:

Выделяется бесконечно малый интервал [ , + d ] и определяется вероятность отказа ОЭ в интервале [ , + d ]:

 

f₀ () = - dP₀ () / d – ПРО ОЭ.

 

ВБР РЭ до момента отказа ОЭ

 

Pр () = P(A₂₂ )

 

ВБР РЭ от момента включения в работу до t

 

Pр (t - ) = P(A₂₃).

 

Тогда ВБР ОЭ в течение наработки [ , + d ] при условии, что ОЭ отказал, равна:

 

Pр () · Pр (t - ) · f₀ () d .

 

Полученное выражение не равно P(A₂ ), поскольку выражает ВБР за выделенный бесконечно малый интервал наработки вблизи .

Поскольку < t, то из полученного выражения искомая вероятность P_р (t) = P(A₂ ), получена интегрированием выражения по всем от 0 до t.

Окончательно:

 

 

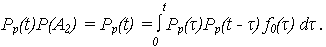
Тогда ВБР резервируемой системы с облегченным резервом:

 

 

Аналогично, ВБР системы, состоящей из n равнонадежных элементов:

 

 

где индекс (n-1)с означает, что ВБР и ПРО относятся к системе, при отказе которой включается рассматриваемый n –й элемент.

При экспоненциальном распределении наработки до отказа элементов составляющие расчетного выражения принимают вид:

 

	Pр () = exp(- p );
	Pр (t - ) = exp { - раб (t - )};
	f0 () = раб exp (- раб · );
	P0 (t) = exp (- раб · t),

 

где _раб – ИО элементов в рабочем режиме; _p – ИО элементов в режиме резерва.

При наличии одного ОЭ и одного РЭ (n = 2), ВБР определяется:

 

 

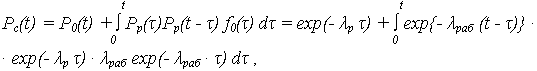
окончательно:

 

P_с (t) = exp (- _раб · t) [ 1 + _раб {1 - exp (- _pt)} / _p ].

 

Для системы из n элементов с экспоненциальной наработкой до отказа

 

 

где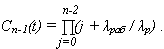

Расчеты для систем с облегченным резервом имеют объективные трудности, поскольку очень трудно учесть как влияет нагрузка, внешние воздействия на характеристики надежности.

Средняя наработка до отказа системы из n элементов:

 

 

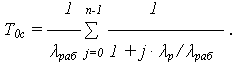
Для практических расчетов систем с облегченным резервированием в случае, если ОЭ имеет распределением наработки P₀ (t) = exp (- _раб · t) и идентичные резервные элементы (РЭ)

 

Pр (t) = exp (- _pt) – для(n - 1) резервных элементов,

ВБР системы может быть приближенно определена по выражению:

 

 

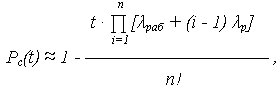
где n – общее число элементов системы.

Например, при n = 2 (k = 1, m = 1)

 

 

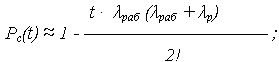
при n = 3 (k = 2, m = 1)

 

 

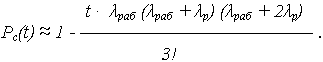
Скользящее резервирование

 

При скользящем резервировании резервный элемент может быть включен взамен любого из отказавших элементов основной системы.

Структура скользящего резервирования:

 

 

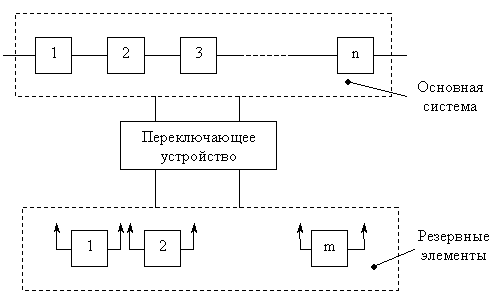
Основная система – n элементов.

Резервная группа – m элементов.

Обычно m < n, т. е. число резервных элементов (РЭ) меньше числа основных (ОЭ), поэтому скользящее резервирование считается активным с дробной кратностью.

Отказ системы наступает в случае, когда число отказавших основных элементов превысит число резервных.

Примером может служить организация линий связи, когда имеется одна резервная линия на несколько основных (в практике, трех).

Рассмотрен случай определения ВБР системы с одним резервным элементом на n элементов основной системы.

Допущение: РЭ и 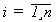элементов основной системы равнонадежны и РЭ не может отказать до момента его включения в работу.

 

 

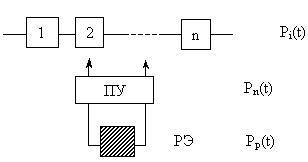
Известны: P_i (t) = P (t); P_n (t); P_p (t).

Получение расчетного выражения для ВБР системы аналогично тому, что было приведено для облегченного резерва:

• выделение возможных состояний системы, при которых она продолжает безотказно работать;
• вычисление вероятностей этих состояний.

События, обеспечивающие безотказную работу (БР) системы в течение (0, t):

A = {БР системы за наработку (0, t)};

A₁ = {БР всех 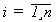элементов основной системы за наработку (0, t) };

A₂ = {БР при условии, что отказал один элемент из 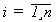при < t, переключающее устройство работоспособно – включение РЭ и БР его на интервале (t - )}.

Событие A выполняется в результате выполнения одного из событий A₁ или A₂

 

A = A₁ A₂.

 

Работа резервного элемента

 

 

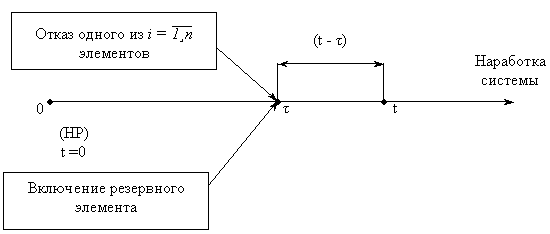
ВБР системы за наработку (0, t) равна:

 

P(A) = P(A₁) + P(A₂),

 

где P(A) = P _с (t);

P(A₁ ) = P₁ (t) = P_0c (t) = P_n (t) – ВБР основной системы (ОС) к моменту t, где P₁ (t) = … = P_n (t) = P (t) – ВБР каждого из 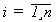элементов;

P(A₂ ) = P₂ (t) – ВБР для события A₂.

Для определения вероятности P(A₂ ), рассмотрим событие A₂:

A¹₂₁ = {отказ одного (первого) из 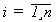элементов ОС при < t};

A¹₂₂ = {БР переключающего устройства (ПУ) до наработки – момента включения РЭ};

A¹₂₃ = {БР РЭ после включения его в работу, т. е. на интервале (t - )}.

Очевидно, что

 

A¹₂ = A¹₂₁ A¹22 A¹₂₃,

 

поэтому

P(A¹₂) = P(A¹₂₁) · P(A¹22) · P(A¹₂₃).

Индекс 1 – отказ 1 элемента ОС.

Соответствующие вероятности:

1. Выделяется бесконечно малый интервал [ , + d ] и определяется ВО ОЭ в интервале [ , + d ]:

 

f()d = - dP() / d .

 

2. ВБР ПУ до момента отказа одного из элементов ОС равна P_п();

3. ВБР РЭ с момента его включения, т. е. за интервал (t - ): Pр (t - ).

Тогда ВБР системы в течение наработки [ , + d ] при отказе первого элемента ОС, равна:

 

f() d · P_п () · P_р (t - )

 

Интегрируя по всем от 0 до t, определяется ВБР системы при условии, что первый из элементов ОС отказал:

 

 

Аналогичные рассуждения можно провести для каждого из n элементов ОС. После отказа одного из элементов, n –1 элементов должны остаться работоспособными.

Поскольку событие A₂, заключающееся в БР системы, подразумевает БР при отказе любого из n элементов ОС, то его можно рассматривать, как

 

 

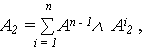
где .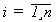

A^{n – 1} – событие, заключающееся в БР оставшихся (n – 1) элементов ОС;

Aⁱ₂ – БР системы при отказе i -го элемента (не только первого) ОС.

 

 

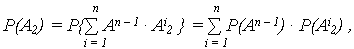
где P(A^{n – 1}) = P^{n – 1}(t).

Поэтому ВБР системы при отказе 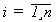элемента ОС выражается:

 

 

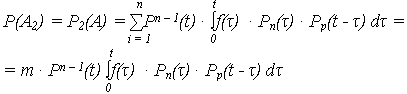
Тогда ВБР системы со скользящим резервом определяется:

 

 

При экспоненциальном распределении наработки до отказа основных и резервных элементов P(t) = exp (- _j t), а также переключающего устройства (ПУ), ВБР системы:

 

P с (t) = [ 1 + n · 0 / п (1 – exp (- п t))] exp (- n 0t),

 

где ₀ – ИО основного и резервного элементов;

_п – ИО переключающего устройства.

Показатель эффективности резервирования:

 

Bр = Pс(t) / P₀с(t) = 1 + n · 0 / п (1 – exp (- пt)),

 

где P₀ с(t) = exp (- n ₀ t) – ВБР основной системы.

При большем числе резервных элементов (m > 1) при определении Pс(t) рассматриваются четыре несовместных события (для m = 2), при которых возможна БР системы и т. п.

 

 

Контрольные вопросы:

1. Что в надежности представляет облегченный резерв и видом какого резервирования он является?

2. Сформулируйте условие работоспособности системы с облегченным резервом?

3. Приведите логическую цепь вывода выражения ВБР системы с облегченным резервом?

4. Что представляет собой скользящее резервирование в надежности, и видом какого резервирования оно является?

5. Сформулируйте условия работоспособности системы со скользящим резервированием и приведите логическую цепь вывода выражения ВБР системы?

 

Лекция 13

Предыдущая567891011121314151617181920Следующая

Поделиться:

Воспользуйтесь поиском по сайту: