Связь логической схемы надежности с графом состояний

 

Переход от логической схемы к графу состояний необходим:

1)при смене методов расчета надежности и сравнении результатов;

2) для оценки выигрыша в надежности при переходе от невосстанавливаемой системы к восстанавливаемой.

Рассмотрим типовые логические структуры надежности. Типовые соединения рассмотрены для невосстанавливаемых систем (граф – однонаправленный, переходы характеризуются ИО ).

Для восстанавливаемых систем в графах состояний добавляются обратные стрелки, соответствующие интенсивностям восстановлений .

 

 

 

Контрольные вопросы:

1. В чем особенности марковского случайного процесса, на основе которого строится расчетная модель для восстанавливаемых объектов и систем?

2. Основные этапы составления расчетной модели?

3. Что представляет собой система дифференциальных уравнений Колмогорова-Чепмена? Объясните смысл каждого из составляющих в дифференциальном уравнении?

4. Поясните мнемоническое правило составления дифференциального уравнения вероятностей состояния (уравнение Колмогорова - Чепмена)?

5. Дайте определение и поясните смысл показателей надежности восстанавливаемых объектов и систем?

6. Поясните, как изменяются показатели надежности восстанавливаемого объекта при изменении интенсивности восстановления?

7. Особенности применения метода дифференциальных уравнений для расчета надежности невосстанавливаемых объектов?

8. На любом из примеров поясните связь графа состояний с логической структурой надежности?

 

Лекция 14

НАДЕЖНОСТЬ ОБЪЕКТОВ ПРИ ПОСТЕПЕННЫХ ОТКАЗАХ. ОСНОВНЫЕ РАСЧЕТНЫЕ МОДЕЛИ

Если отказы происходят из-за случайных изменений параметров объекта во времени t (в общем случае в функции любой монотонно возрастающей величины - наработки), то эти отказы называются постепенными или параметрическими.

Надежность определяется вероятностью безотказной работы (ВБР) P(t), которая является функционалом некоторого случайного процесса (t), характеризующего изменение параметров объекта во времени. ВБР объекта на отрезке времени [t₀, t] равна вероятности нахождения процесса (t) в заданной допустимой области в течение этого отрезка времени:

 

 

(1)

 

 

Объект является работоспособным, пока изменяющаяся во времени величина не достигает границы допустимой рабочей области .

 

Постановка задачи. Основные понятия и определения

 

Постановка задачи: рассмотрение моделей процессов развития отказов для задач типа "нагрузка - прочность" и "параметр - поле допуска". Кроме решения основной задачи надежности - нахождения распределения наработки до отказа, определяется момент времени, в который объект должен быть подвергнут ремонту, профилактике или регулировке в целях сохранения работоспособности.

Рассматриваемые расчетные модели универсальны и могут использоваться для прогнозирования отказов различных объектов (механических, электромеханических и электронных), поэтому основные технические параметры, характеризующие работоспособность объекта и являющиеся его мерой качества, назовем определяющими параметрами (ОП).

При решении конкретной задачи в качестве ОП Х могут выступать величины деформации или механического напряжения, электрические или геометрические параметры (характеристики) объекта.

В общем случае ОП может быть вектором, т.е. иметь несколько составляющих. Предельные значения, устанавливаемые на каждый ОП объекта, являются допустимыми значениями ОП, которые ограничивают рабочую область (поле допуска).

Пока значения векторного ОП объекта находятся внутри многомерной рабочей области, объект считается работоспособным. Однако с течением времени под влиянием факторов, связанных со старением, изнашиванием или разрегулированием конец вектора Х(t) может достичь границы рабочей области. При этом объект теряет работоспособность (происходит отказ). Из-за случайного характера внешних и внутренних факторов, влияющих на процесс приближения объекта к отказам, характер изменения ОП во времени и время достижения каждым ОП своей границы также являются случайными. Поэтому наиболее полно случайный процесс возникновения постепенных отказов объекта по каждому ОП описываетя соответствующей плотностью распределения времени пересечения ОП границы рабочей области, иначе - плотностью распределения времени до отказа.

В практике эксплуатации объекта важнее знать не плотность распределения времени до отказа, а конкретное время сохранения работоспособности, в течение которого ОП не достигнет границы рабочей области.

В общей постановке задачи границу рабочей области можно рассматривать как систему случайных величин или векторный случайный процесс.

Рассмотрим характер случайного процесса приближения к отказу на примере объекта, работоспособность которого определяется скалярным ОП (одной координатой векторного ОП). При этом пространство ОП Х будет одномерным, а рабочая область ограничена отрезком прямой (предельное значение ОП X_п). Пусть имеется множество j = , одинаковых объектов, одновременно включенных в работу (при t = 0), и ОП каждого объекта измеряется в одни и те же моменты времени t_i (i = ).

Процесс изменения ОП одинаковых объектов при эксплуатации будем рассматривать как случайную функцию Х(t) времени. Для каждого j-го объекта (j = ) изменение ОП является реализацией (составляющей) Х_j (t) случайной функции Х(t). Точки пересечения реализаций Х_j (t) случайного процесса с границей X_п рабочей области (поля допуска) соответствуют моментам времени отказов j-х объектов. Поэтому случайный характер возникновения постепенных отказов при эксплуатации одинаковых объектов описывается плотностью распределения f{X(t)} времени пересечения ОП границы X_п, т.е. плотностью распределения времени до отказа.

Если с момента включения в работу (при t = 0) путем измерений с одинаковой t = t_{i +1} - t_i = t_i - t_{i -1} или различной периодичностью (интервалом) t контролировать значения ОП j = объектов, то можно предсказать (экстраполировать) дальнейшее изменения ОП и, следовательно, момент наступления отказа. Это позволит организовать техническое обслуживание группы объектов, т.е. обеспечить упреждающий вывод в текущий или капитальный ремонт или на регулировку. Интервал времени от начала эксплуатации объекта t=0 до момента, когда выход отдельных реализаций Х_j (t) случайного процесса Х(t) за границу X_п рабочей области становится частым явлением, называется временем сохранения работоспособности tс. Правый конец интервала tс определяется абсциссой характерной точки кривой плотности f{X(t)} распределения времени до отказа, начиная с которой наблюдается резкий рост кривой.

Таким образом, определяя с помощью средств технического контроля в фиксированные моменты времени t₁,..., t_k tс значения ОП j = 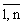однотипных объектов, можно получить реализации Х_j (t) реального процесса изменения ОП. При этом измеренные в t_i, i = моменты времени значения ОП являются случайной величиной Х_i = Х(t)i = {x₁, x₂,..., x_N}t_i, характеризуемой плотностью распределения f(X)i и оценками числовых характеристик - средним (математическим ожиданием) m_Xi и дисперсией D_Xi. Cлучайную величину {X}i назовем значением реализаций ОП при i-м контроле.

Итак, располагая информацией о реальном процессе изменения ОП для времени t_k < tс на этапе эксплуатации или имея ту же информацию об аналогах проектируемого объекта на стадии проектирования, возможно аналитически рассчитать время сохранения работоспособности объекта, т.е. сделать обоснованный прогноз о работоспособности в будущем. Это позволит своевременно предупредить отказ, а также управлять состоянием сложных объектов путем замены их элементов резервными, либо путем изменения рабочих режимов объектов.

 

Предыдущая567891011121314151617181920Следующая

Поделиться:

Воспользуйтесь поиском по сайту: