 |
Лабораторная работа №3. Определение ускорения свободного падения при помощи оборотного маятника. Порядок выполнения работы
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА №3
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ ПРИ ПОМОЩИ ОБОРОТНОГО МАЯТНИКА
Большинство косвенных методов измерения g основано на использовании известной формулы для периода колебаний физического маятника:
(1)
Здесь J – момент инерции маятника относительно оси качания, m – его масса, l – расстояние от центра масс до точки подвеса. Измерение периода можно выполнить с большой точностью, чего обычно не удаётся сделать для величин J и l.
Достоинством рассматриваемого метода является возможность исключить эти величины из расчётной формулы.
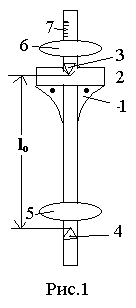
| Оборотный маятник изображён на рис. 1. Здесь 1-настенный кронштейн, на котором смонтированы подушки 2 для опорных призм маятника 3 и 4, жёстко закреплённых на стержне Расстояние между призмами lо известно. На металлическом стержне между опорными призмами неподвижно закреплена чечевица 5, а чечевица 6 может перемещаться по шкале 7 и закрепляться в нужном положении. Период колебаний маятника можно менять, передвигая эту подвижную чечевицу. Измеряют периоды колебаний маятника Т1 и Т2 относительно призм 3 и 4 при разных положениях чечевицы. Допустим, что удалось найти такое положение чечевицы 6, при котором |
периоды колебаний маятника Т1 и Т2 совпадают. Тогда:
(2)
Отсюда следует:
(3)
По теореме Штейнера:
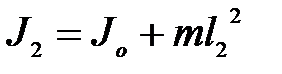(4)
Здесь Jo – момент инерции маятника относительно оси, проходящей через его центр тяжести и параллельно оси качаний. Исключая из (3) и (4) Joи m, получаем:
(5)
|
|
|
Обозначая l1 + l2 = lo – расстояние между призмами 3 и 4, окончательно получаем:
(6)
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Помещаем подвижную чечевицу 6 на четвёртом делении шкалы 7, определяет время t1 50 колебаний маятника на призме 3, затем, повернув маятник, определяем время t2 50 колебаний на призме 4, отклоняя маятник на небольшой угол от вертикали. Находим периоды колебаний:
Записываем данные в таблицу.
2. Перемещаем чечевицу 6 на 2 см вверх и повторяем измерения. Так поступаем 4 раза, т. е. определяем периоды колебаний маятника, когда чечевица 6 стоит на делениях 4, 6, 8, 10. Все результаты заносим в таблицу.
ТАБЛИЦА
| Положения чечевицы х | t1 c | t2 c | T1 c | T2 c |
ЗАДАНИЕ
1. Построить график зависимости Т1 и Т2 от положения чечевицы х в одной системе координат в виде двух плавных кривых.
2. По точке пересечения зависимостей Т1(х) и Т2(х) определить величину Тф.
3. Вычислить g по формуле (6).
Примечание: значение lo= 0. 73 м
ЛАБОРАТОРНАЯ РАБОТА №4
ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ПРИ ПОМОЩИ МАЯТНИКА ОБЕРБЕКА
Основное уравнение вращательного движения тела относительно неподвижной оси вращения имеет вид:
(1)
Здесь М – сумма проекций на ось вращения моментов всех внешних сил, действующих на тело, w - его угловая скорость, J – момент инерции тела относительно данной оси. Для однородного твёрдого тела момент инерции представляет собой постоянную величину. Поэтому уравнение (1) можно записать в виде:
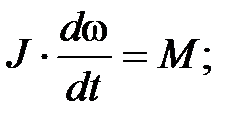
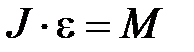(2)
Величина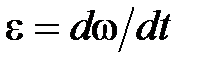 
представляет собой угловое ускорение.
Момент инерции J играет во вращательном движении ту же роль, что и масса m тела в его поступательном движении. Масса отражает инертность тела в поступательном движении, момент инерции отражает инертность тела в его вращательном движении. Чем больше J, тем труднее заставить вращающееся тело изменить угловую скорость 
.
|
|
|
| Маятник состоит из четырёх спиц, укреплённых на втулке под прямыми углами На каждой спице закреплены грузы А. Втулка и два шкива различных радиусов (R1иR2) насажены на общую ось. Ось закреплена в подшипнике, так что вся система может свободно вращаться вокруг горизонтальной оси. Момент инерции маятника можно изменять, передвигая грузы вдоль спиц. В отсутствие вращающего момента М маятник находится в состоянии безразличного равновесия. Для приведения маятника во вращение надо приложить к нему момент сил М. Это |
Основное уравнение вращательного движения (2) удобно исследовать с помощью маятника Обербека (рис. 1)
можно сделать с помощью нити, намотанной на один из шкивов.
На нити подвешивается груз массы m, натягивающий нить. Если натяжение нити равно Т, то момент сил, действующий на маятник, равен:
Величина Т определяется следующим образом. При вращении маятника, груз начинает опускаться с ускорением а. Уравнение движения опускающегося груза выглядит следующим образом:
Следовательно:
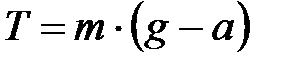(3)
Соответственно, момент внешних сил, приложенных к маятнику, равен:
(4)
Ускорение а в данном случае является тангенциальным ускорением аt точек обода шкива, с которого сматывается нерастяжимая, не скользящая по шкиву нить. Связь между тангенциальным и угловым ускорением даётся формулой:
(5)
Ускорение а можно вычислить, измерив время t падения груза с известной высоты h. Падение груза является равноускоренным, поэтому для движения груза справедливо уравнение:
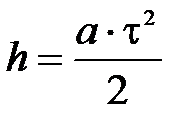(6)
Отсюда:
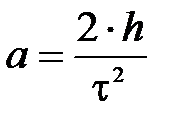(7)
В действительности, при вращении маятника, всегда существует сила трения в подшипнике. Эта сила создаёт момент силы Мтр. С учётом момента силы трения уравнение (2) может быть записано в виде:
|
|
|
Приведённое уравнение записывается в виде:
(8)
|
|
|
