 |
Описание установки. Порядок выполнения работы. Лабораторная работа №11. Определение модуля Юнга вещества. По прогибу
|
|
|
|
ОПИСАНИЕ УСТАНОВКИ
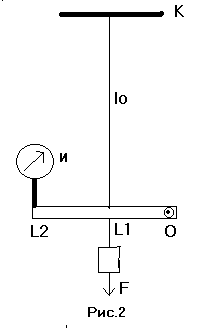
| Схема установки представлена на рис. 2. Металлическая проволока длины l0 своим верхним концом укреплена на кронштейне К. Нижний конец проволоки связан с плечом ОL1 горизонтального рычага, имеющего ось вращения О. Плечо рычага ОL2 соединено со стрелочным измерителем И, предназначенным для измерения деформации растяжения проволоки. К нижнему концу проволоки с помощью крючка подвешивается груз F, вызывающий абсолютную деформацию проволоки ∆ l, Посредством рычага деформация проволоки передается на измеритель И, стрелка которого отклоняется при этом на ∆ х. Величина ∆ l связана с ∆ х соотношением: |
(3)
Измеряя ∆ х и вычисляя ∆ l для разных F, можно построить график зависимости ε от σ . В соответствии с уравнением (2), наклон этого графика позволяет определить модуль Юнга E.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Занести в таблицу указанное в лаборатории значение длины проволоки l0, вычислить и записать в таблицу площадь поперечного сечения Sпо приведённому в лаборатории значению диаметра d и отношение плеч рычагаОL1/ОL2.
2. При ненагруженной проволоке (F=0) определить начальное х0 положение стрелки измерителя И и занести в таблицу.
3. Последовательно нагружая проволоку грузом от 1 Н до 6 Н, каждый раз определять положение х указателя, занося их в таблицу.
4. Последовательно снимая грузы от 6 Н до 0, определять значения х при разгрузке проволоки. Эти данные также заносить в таблицу.
5. Определить средние значения х, полученные при нагрузке и разгрузке проволоки для каждого значения F, определить величины ∆ х= х – х0, соответствующие каждой нагрузке. Из этих данных по уравнению (3) определить значения абсолютной деформации проволоки ∆ l при разных нагрузках и величины относительной деформации ε. Все полученные значения занести в соответствующие столбцы таблицы.
|
|
|
6. Зная значения нагрузки F и площади поперечного сечения S проволоки, вычислить напряжение σ = F/S для каждой нагрузки и занести в таблицу.
7. По полученным данным на миллиметровой бумаге построить график зависимости ε (ордината) от σ (абсцисса). В соответствии с уравнением (2), он представляется прямой линией, наклон которой к оси абсцисс равен 1/E.
8. По наклону этой прямой определить значение модуля Юнга Е проволоки. Погрешность ∆ Е определить графически.
9. Записать окончательный результат в виде:
Е = (Еср + ∆ Еср) Па
ТАБЛИЦА.
l0 =1, 5 м, S =1, 5× 10-8 м2, OL1/ОL2 =0, 41
|
№ | нагрузка | х, мм | Dх, мм | Dl, мм | e | |||
| F, H | s, Па | нагр | разгр | средн | ||||
| 5, 1 | 5, 1 | |||||||
| 0, 48 | 5, 48 | 5, 30 | ||||||
| 1, 96 | 5, 86 | 5, 82 | ||||||
| 2, 94 | 6, 32 | 6, 28 | ||||||
| 3, 92 | 6, 75 | 6, 53 | ||||||
| 4, 9 | 7, 2 | 7, 03 | ||||||
| 5, 88 | 7, 53 | 7, 38 | ||||||
ЛАБОРАТОРНАЯ РАБОТА №11
ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ВЕЩЕСТВА
ПО ПРОГИБУ
Деформация твёрдого тела является результатом изменения взаимного расположения частиц, составляющих тело, и расстояний между ними при воздействии внешней силы. При деформации в веществе возникают силы, стремящиеся восстановить первоначальную форму тела после прекращения действия силы. Такая деформация называется упругой обратимой деформацией. Простейшим видом упругой деформации является деформация растяжения тела вдоль некоторого направления (одноосная деформация).
|
|
|
| Для упругой обратимой деформации растяжения стержня справедлив закон Гука:
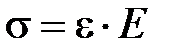 (1)
В этой формуле s =F/S – напряжение, возникающее в стержне, имеющем площадь поперечного сечения S, F – сила, приложенная
|
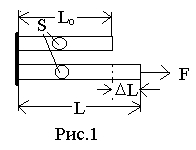
к стержню и растягивающая его (рис. 1), e = (L-Lo)/Lo = DL/Lo– относительная деформация стержня, DL = L – Lo– его абсолютная деформация. Множитель пропорциональности Е называется модулем Юнга материала. Модуль Юнга является одной из основных характеристик упругих свойств тела. Модуль Юнга показывает, какое напряжение s надо приложить к телу, чтобы вызвать его относительное удлинение e = 1 (растянуть стержень вдвое). Размерность модуля Юнга Е совпадает с размерностью давления (см. также лаб. работу №10).
| Определение модуля Юнга возможно многими методами. В частности, эта упругая характеристика материала может быть найдена при изучении прогиба стержня под действием силы F, приложенной к нему в перпендикулярном направлении. При этом стержень изгибается в виде некоторой дуги. Тип деформации при прогибе и при одноосном растяжении в принципе одинаков. |
Прогиб стержня под действием силы F характеризуется стрелой прогиба l (рис. 2). Прогиб стержня l определяется величиной приложенной силы F и упругими свойствами образца, т. е. модулем Юнга Е. Связь между l, F и Е даётся уравнением:
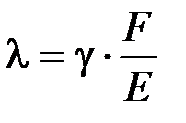(2)
В этом уравнении постоянная g определяется геометрией образца:
(3)
a – длина стержня, определяемая как расстояние между опорами, на которых покоится стержень, b – ширина стержня, c – его толщина.
Для нахождения модуля Юнга Е соотношение (2) удобно переписать в виде:
(4)
В координатах F (ордината) - 
(абсцисса) выражение (4) представляет собой уравнение прямой, проходящей через начало координат: F = k·l. Угловой коэффициент зависимости F от l равен: k =E / s. Вычислив угловой коэффициент k (определяемый как тангенс угла наклона прямой к оси абсцисс, но имеющий определённый физический смысл и единицы измерения), можно найти значение модуля Юнга:
|
|
|
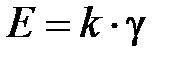(5)
|
|
|
