 |
Лабораторная работа № 9. Определение коэффициента трения качения методом наклонного маятника. В работе определяется коэффициент трения μk качения шара по плоский поверхности. Согласно уравнению (1), коэффициент трения качения имеет размерность длины.
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА № 9
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ КАЧЕНИЯ МЕТОДОМ НАКЛОННОГО МАЯТНИКА
При движении некоторого тела относительно другого возникает сила, направленная в сторону, противоположную движению и препятствующая этому движению. Такая сила называется силой трения. Природа сил трения очень сложна и связана с физико-механическими и электрическими взаимодействиями тел в области их контакта. Для описания сил трения используют эмпирические соотношения, полученные первоначально Г. Амонтоном и Ш. Кулоном. Для силы трения качения:
Fk = (μ к·N)/R (1)
Где N – сила нормального давления тела на поверхность, по которой оно движется, μ к – коэффициент трения качения, R – радиус катящегося шара.
В работе определяется коэффициент трения μ k качения шара по плоский поверхности. Согласно уравнению (1), коэффициент трения качения имеет размерность длины.
Поставленная цель достигается использованием наклонного маятника, который представляет собой сочетание математического маятника с наклонной плоскостью.
ОПИСАНИЕ УСТАНОВКИ
.
Схема наклонного маятника представлена на рис. 1. Здесь α –угол наклона плоскости к горизонту, φ – угол отклонения маятника от положения равновесия. В этом случае:
Fk = (μ к·m·g·cosα )/R (2)
В основе метода определения μ к лежит закон изменения механической энергии ∆ W, согласно которому в замкнутой механической системе изменение энергии равно работе неконсервативных сил. Так, например, для шара, катящегося по поверхности, справедливо выражение:
|
|
|
∆ W = Fк·S = (μ k·N·S)/R (3)
где S – путь, пройденный катящимся шаром.
Полная механическая энергия шара в момент максимального отклонения от положения равновесия равна его потенциальной энергии в поле силы тяжести, которая связана с углами φ и α соотношением:
W = m·g·L·(1 – cosφ )·sinα (4)
Здесь L – длина нити маятника.
Если маятник отклонить на некоторый угол φ 0 и отпустить без толчка, он начнет колебаться около положения равновесия. При наличии силы трения, по истечении n колебаний, угол отклонения маятника станет равным φ n. Потеря полной энергии системы при этом будет равна:
∆ W = Wn – W0 = m·g·L·(cosφ n – cosφ 0)·sinα (5)
Если обозначить через Si путь, проходимый маятником от положения равновесия до максимума при каждом колебании влево или вправо, то весь путь, пройденный маятником, будет равен:
S =2·( S1 + S2 +……+ Si +…….. + Sn)
Вследствие постоянства силы трения качения пути Si убывают по линейному закону. Это означает, что последовательность значений Si представляет собой арифметическую прогрессию, сумма которой, а, cледовательно, и весь путь S равны:
S = 2·n·(S1 + Sn)/2 = n·L·(φ 0 + φ n). (6)
Здесь использовано соотношение S = φ ·L, следующее из определения радианной меры угла.
Решая совместно уравнения (1) – (6), для коэффициента трения качения получаем выражение:
 (7)
(7)
Если дождаться полной остановки маятника, то угол jn станет равным нулю, и формула (7) упростится:
 (8)
(8)
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. С помощью штангенциркуля найти радиус R шара. Результат занести в таблицу.
|
|
|
2. Руководствуясь рис. 1, определить тангенс угла наклонной плоскости маятника к горизонту. Измерения l и hпроводить с помощью линейки. Результат занести в таблицу.
3. Отклоняя маятник на угол φ 0, определить число n колебаний маятника слева направо и обратно до его полной остановки (φ n = 0). Измерения провести для трех начальных углов φ 0 (указаны в лаборатории). Результаты определения занести в таблицу.
4. Для каждого угла φ 0 по формуле (8) рассчитать величину μ к, его среднее значение (μ к)ср и среднюю погрешность измерений (∆ μ к)ср. Результаты расчета занести в таблицу. Следует иметь в виду, что в СИ единицей измерения угла является радиан.
5. С учетом п. 3, расчет μ к следует проводить по формуле (8).
ТАБЛИЦА
tgα =1, 27, R =0, 029 м
| № | jо, | n | mк, м | Dmк, м | |
| град | рад | ||||
| Среднее: | |||||
ЛАБОРАТОРНАЯ РАБОТА № 10
ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА МЕТАЛЛА МЕТОДОМ ОДНООСНОГО РАСТЯЖЕНИЯ
Если к металлическому стержню длины l0, имеющему площадь поперечного сечения S, приложить растягивающую силу F, то его длина увеличится до некоторого значения l (рис. 1):

При небольших растяжениях (в области т. н. упругой деформации) между этими величинами существует связь:
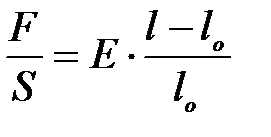 (1)
(1)
Отношение F/S = σ представляет собой напряжение, возникающее в стержне при приложении силы F, l – l0 = ∆ l – абсолютную деформацию стержня, (l – l0)/l0 = ∆ l/l0 = ε – его относительную деформацию.
В терминах напряжения σ и относительной деформации ε уравнение (1) записывается в виде:
σ = ε ·E (2)
Множитель пропорциональности Е называется модулем Юнга (или модулем одноосного растяжения). Единицей измерения Е является Паскаль. Численно модуль Юнга равен напряжению σ , которое вызывает относительную деформацию ε = 1 , т. е. стержень растягивается вдвое. Однако такие растяжения для любого металла практически недостижимы (стержень рвется при ε ‹‹ 1). Модуль Юнга Е является характеристикой упругих и прочностных свойств материала.
|
|
|
Целью работы является определение модуля Юнга металла.
Поставленная цель достигается изучением деформации растяжения металлической проволоки под действием приложенной нагрузки.
|
|
|


