 |
Таблица 1. Лабораторная работа № 6. Определение радиуса кривизны вогнутой. Поверхности методом катающегося шарика. Порядок выполнения работы
|
|
|
|
ТАБЛИЦА 1
| m, кг | D, м | J1, кг·м2 |
| 0. 365 | 0. 78 |
ТАБЛИЦА 2
| n | Jn, кг·м2 | jn | tn, с | Tn, с | Tn2, с2 |
| 8. 56 | |||||
| 11. 87 | |||||
| 14. 05 | |||||
| 16. 19 | |||||
| 18. 34 |
ТАБЛИЦА 3
| t, Н·м/рад | jxд | txд, c | Тхд, c | Jхд кг·м2 | Δ Jx кг·м2 |
| 19. 37 |
ЛАБОРАТОРНАЯ РАБОТА № 6
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ВОГНУТОЙ
ПОВЕРХНОСТИ МЕТОДОМ КАТАЮЩЕГОСЯ ШАРИКА
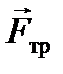
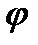
Если шарик массой m и радиусом r, находящийся на вогнутой поверхности в поле силы тяжести, вывести из равновесия и предоставить самому себе, то он будет совершать колебания относительно положения равновесия (точка Р на рис. 1а). При малых амплитудах период колебаний шарика Т зависит от радиуса кривизны поверхности.
На шарик вне положения равновесия действуют три силы: сила тяжести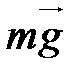 
; нормальная составляющая реакции опоры 
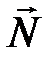; сила трения 
(предполагается, что шарик вращается без проскальзывания).
Движение шарика можно рассматривать как суперпозицию двух движений (рис. 1a): поступательного движения центра масс по дуге окружности радиуса R и вращательного движения вокруг оси, проходящей через центр масс перпендикулярно плоскости рисунка. Оба эти движения являются ускоренными. Обозначим ускорение поступательного движения аt, угол поворота шарика вокруг своей оси a, угловое ускорение вращения шарика относительно этой оси eш. Поступательное движение шарика по вогнутой поверхности можно также рассматривать как вращение тела с угловым ускорением eо по окружности, радиус R которой равен радиусу Rx вогнутой поверхности, уменьшенному на радиус r шарика (см. рис. 1а):
|
|
|
R = Rx – r.
Поступательное движение шарика происходит в согласии со вторым законом Ньютона, который, в проекции на направление касательной к окружности, запишется в виде (рис. 1б):
(1)
Основное уравнение динамики вращательного движения шарика дает:
(2)
где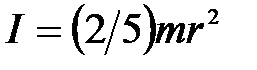 
- момент инерции шара, Fтр·r-момент сил трения, возникающих при качении шарика по вогнутой поверхности.
В качестве обобщенной координаты, задающей положение шарика, выберем угол j (рис. 1б). Угловое ускорение eо центра масс шарика относительно центра кривизны вогнутой поверхности связано с касательным ускорением аt формулой:
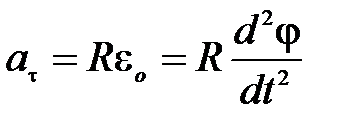(3)
При качении без проскальзывания угол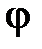 
связан с углом поворота шарика 
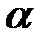относительно его центра:
j× R = a× r (4)
Дифференцируя уравнение (4) дважды по времени, получаем связь между ускорениями eш и eо:
(5)
Решая совместно (1) – (5), получим дифференциальное уравнение для обобщенной координаты j:
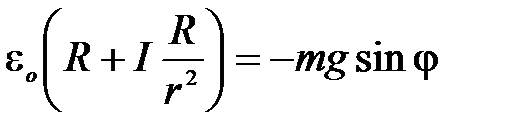, или 
,
которое, в приближении малых амплитуд (малых углов j, когда можно положить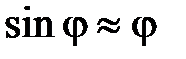 
), принимает вид уравнения гармонических колебаний:
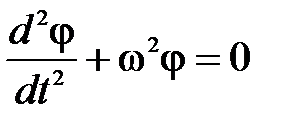, где 
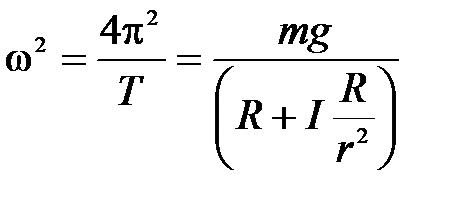(6)
Учитывая, что 
, получим: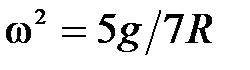 
Откуда: 
Окончательно, формула для расчета радиуса кривизны вогнутой поверхности будет иметь вид:
(7)
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. С помощью штангенциркуля измерить радиус шарика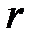 
. Результат измерения занести в таблицу.
2. Положить шарик на вогнутую поверхность несколько в стороне от положения равновесия. С помощью секундомера измерить время 6 полных колебаний. Опыт проделать три раза. Значение времени t и число колебаний n занести в таблицу.
|
|
|
3. Для каждого случая вычислить период колебаний шарика по формуле
4. Найти среднее значение периода Тср колебаний шарика.
5. Выполнить пункты 1 – 4 для каждого шарика.
6. Для каждого Тср по формуле (6) вычислить радиус кривизны Rx вогнутой поверхности. Результаты занести в таблицу.
7. Найти среднее значение радиуса кривизны ( Rx)ср и оценить абсолютную погрешность (DRx)ср по методу прямого измерения. Результаты занести в таблицу.
8. Записать окончательный результат с учётом погрешности измерений.
|
|
|
