 |
Изменение масштаба аргумента функции
|
|
|
|
Симметрия
Как уже отмечалось, спектр дискретного периодического сигнала является периодическим. Кроме того, сохраняется и свойство симметрии, которым обладает спектр непрерывного вещественного сигнала (
). Поэтому
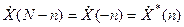. (5)
Гармоника с нулевым номером (постоянная составляющая), как видно из (3), представляет собой сумму отсчетов последовательности на одном периоде:
(6)
Если N четно, то амплитуда гармоники с номером N/2 является суммой отсчетов с чередующимися знаками:
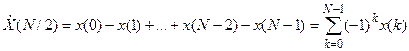
Согласно (5), спектр является «сопряженно-симметричным» относительно N/2, то есть содержит ровно такое же количество информации, что и сам сигнал. В самом деле, исходная последовательность представляется набором из N вещественных чисел. Спектр же представляется набором из N/2 (вторая половина взаимно-однозначно связана с первой) комплексных чисел, каждое из которых с информационной точки зрения эквивалентно двум вещественным. Если же исходная последовательность {х(k)} не является вещественной, симметрия спектра отсутствует и N комплексным отсчетам во временной области соответствует N комплексных отсчетов в спектральной области.
ДПФ произведения последовательностей
Возьмем две последовательности отсчетов {х1(k)} и (x2(k)} одинаковой длины N и вычислим результат их поэлементного умножения:
.
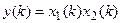Если применить к этой формуле прямое ДПФ, получится следующее выражение:
. (7)
ЗАМЕЧАНИЕ ----------------------------------------------------------------------------------------
При выполнении вычислений по формуле (7) могут понадобиться значения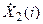 
с номерами i выходящими за рамки диапазона 0…N-1. В этом случае следует воспользоваться свойством периодичности спектра: 
.
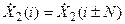Это выражение представляет собой круговую свертку спектров 
и 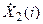. Итак, как и для непрерывного преобразования Фурье, спектр произведения является сверткой спектров.
|
|
|
При п= 0 из (7) получается дискретный аналог теоремы Рэлея (см. «Энергетические расчеты в спектральной области»):
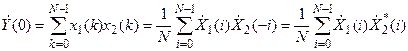. (5.8)
При выводе формулы (8) были использованы соотношения (5) и (6).
Если, кроме того, последовательности {x1(k)} и {x2(k)} совпадают, то есть x1{k)=x2(k)=x(k) для всех k=0...N-1, из (5.8) получается дискретный аналог равенства Парсеваля (см.«Энергетические расчеты в спектральной области» и формулу 
:
.
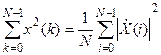Круговая свертка
Так как мы рассматриваем периодические последовательности, то и суммирование при вычислении свертки таких последовательностей следует производить по одному периоду. Такую операцию называют круговой сверткой:
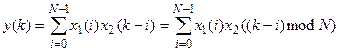. (9)
ЗАМЕЧАНИЕ ---------------------------------------------------------------------------------------
В этой формуле выражение (k-i)modN означает взятие (k-i) по модулю N, то есть вычисление остатка от деления (k-i) на N.
Подставив выражение (9) в (3), легко убедиться, что круговая свертка периодических временных последовательностей соответствует перемножению их спектров:
. (10)
ЗАМЕЧАНИЕ ----------------------------------------------------------------------------------
Круговую свертку периодических последовательностей не следует путать с линейной сверткой, являющейся основой алгоритма дискретной фильтрации.
Как и в случае линейных систем с постоянными параметрами, знание импульсной характеристики позволяет проанализировать прохождение через дискретную систему любого сигнала. Действительно, прежде всего заметим, что произвольный сигнал {х(к)} можно представить в виде линейной комбинации единичных отсчетов:
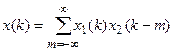
Выходной сигнал, исходя из линейности и стационарности рассматриваемой системы, должен представлять собой линейную комбинацию импульсных характеристик:
(*)
Выражение (*) называется дискретной сверткой (точнее, дискретной линейной сверткой — ее не следует путать с круговой сверткой). Для физически реализуемой системы h(k) - 0 при k < 0, поэтому верхний предел суммирования в формуле (*) можно заменить на к
|
|
|
Это означает, что система при вычислении очередною отсчета может оперировать только прошлыми значениями входного сигнала и еще ничего не знает о будущих.
|
|
|
