 |
Классификация сигналов по спектру
|
|
|
|
Спектральные характеристики сигнала описывают его частотную структуру. Реализация случайного процесса X(t) при условии интегрируемости в интервале 
может быть представлена преобразованием Фурье или комплексным спектром
. (6.61)
Модуль | X (∞) |, называемый спектром сигнала, определяют с помощью анализаторов гармоник спектра, при этом определяется текущий спектр X (j∞, Т), являющийся случайной функцией:
. (6.62)
где Т — время преобразования.
Важнейшей энергетической характеристикой является спектральная плотность среднего значения квадрата сигнала, или спектральная плотность мощности сигнала:
, (6.63)
где среднее значение квадрата сигнала в интервале частот от 
до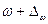 
;
где 
— составляющая сигнала X (t), которая имеет частоты в интервале от до 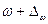(ее можно получить, пропуская сигнал через полосовой фильтр с граничными частотами и 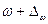, среднее значение ее квадрата в полосе частот от до 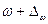получают возведением в квадрат сигнала на выходе полосового фильтра и последующим его осреднением).
Спектральная плотность мощности сигнала может быть получена из автокорреляционной функции 
прямым преобразованием Фурье:
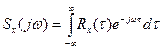
или, принимая во внимание, что автокорреляционная функция является четной,
.
Спектральная плотность мощности сигнала обладает следующими свойствами:
является действительной и неотрицательной функцией;
при ограниченной дисперсии случайного сигнала 
.
Среднее значение сигнала можно выразить через спектральную плотность мощности с помощью дельта-функции:
. (6.64)
Интеграл от спектральной плотности мощности случайного сигнала равен среднему значению его квадрата
(6.65)
Таким образом, среднее значение квадрата сигнала равно суммарной площади под кривой спектральной плотности как функции частоты.
|
|
|
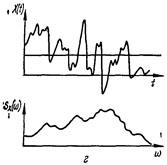
Рис. 6.19. Энергетические спектры реализаций четырех сигналов:
а — гармонического, б — суммы гармонического сигнала и шума, в — узкополосного случайного, г — широкополосного случайного.
Спектральная плотность сигнала на входе 
и выходе 
линейного звена с постоянными параметрами связана соотношением
, (6.66)
где 
— амплитудно-частотная характеристика звена.
Следовательно, если известны или измерены любые две из трех функций , и , то третья может быть определена из (6.66). Однако в этом случае определяется только абсолютное значение частотной характеристики. Для получения ее комплексного значения необходимо найти взаимный спектр сигналов.
Спектральная плотность мощности сигнала дает возможность прежде всего установить его частотную структуру и доминирующую частотную область.
Спектральная плотность мощности сигнала, кроме этого, также, как и плотность вероятности и автокорреляционная функция, используется для идентификации исследуемых сигналов. С ее помощью можно установить, является ли данный сигнал гармоническим или случайным. Покажем это на примере сравнения энергетических спектров реализаций четырех сигналов, представленных на рис. 6.19.
Энергетический спектр гармонического сигнала с частотой 
, представляется дельта-функцией при 
, (рис. 6.19, а) и определяется по формуле
, (6.67)
где 
— дельта-функция на частотной оси.
Энергетический спектр суммы гармонического сигнала и шума (рис 6.19, б) представляется в виде суммы дельта-функции и пологого энергетического спектра. Энергетический спектр узкополосного случайного сигнала имеет характерный пик в области основной частотной составляющей и пологую часть (рис 6.19, в).
Указанные особенности энергетического спектра дают возможность различать гармонический, широкополосный и другие сигналы.
|
|
|
Энергетический спектр широкополосного сигнала (рис. 6.19, г) представляется обычно относительно пологой кривой. В идеальном случае для предельно широкополосного сигнала в виде белого шума энергетический спектр одинаков на всех частотах и представляется горизонтальной прямой.
Терминология
Сигнал характеризуется диапазоном частот: мин-мах.
Спектральный анализ характеризуется разрешающей способностью.
Верхняя частота сигнала определяет необходимую частоту дискретизации – по теореме отсчетов. Должна быть достаточно большой, что бы избежать существенных искажений из-за наложения спектров при дискретизации.
Время анализа (окно анализа, если размерность не время) или количество отсчетов определяется наиболее низкой частотой сигнала или необходимой разрешающей способности по частоте.
Разрешающая способность по частоте(шкалы измерения) определяется следующим выражением
,
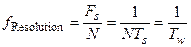но реальная погрешность оценивания зависит от анализируемого сигнала.
В простейшем случае - длительность окна соответствует основному периоду (самой нижней частоте входящей в исследуемый сложный сигнал), а частота дискретизации по теореме отсчетов.
Если есть возможность сделать значительный запас по частоте дискретизации и времени наблюдения, то спектральный анализ может быть выполнен достаточно точно, ценой завышенного количества произведенных математических операций.
Но если количество отсчетов ограничено(временем эксперимента, и пр.), неизвестны моменты начала и окончания циклов периодического процесса (собственно одна из задач анализа- это определение начальных фаз гармоник) и в сигнале присутствует случайная составляющая, то это приводит к различного рода погрешностям.
|
|
|
