 |
Дискретное преобразование Фурье
|
|
|
|
Рассмотрим, что представляет собой спектр дискретного периодического сигнала.
Итак, пусть последовательность отсчетов {x(k)} является периодической с периодом N:
x(k + N) = x(k) для любого k.
Такая последовательность полностью описывается конечным набором чисел, в качестве которого можно взять произвольный фрагмент длиной N, например { x(k), k = 0, 1,..., N - 1}. Поставленный в соответствие этой последовательности сигнал из смещенных по времени дельта-функций:
(1)
также, разумеется, будет периодическим с минимальным периодом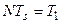 
.
Так как сигнал (1) является дискретным, его спектр должен быть периодическим с периодом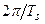 
.
Так как этот сигнал является также и периодическим, его спектр, должен быть дискретным с расстоянием между гармониками, равным 
.
Итак, периодический дискретный сигнал имеет периодический дискретный спектр, который также описывается конечным набором из N чисел (один период спектра содержит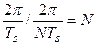 
гармоник).
Рассмотрим процедуру вычисления спектра периодического дискретного сигнала. Так как сигнал периодический, будем раскладывать его в ряд Фурье.
Коэффициенты Х(п) этого ряда, согласно общей формуле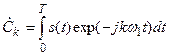 
, равны
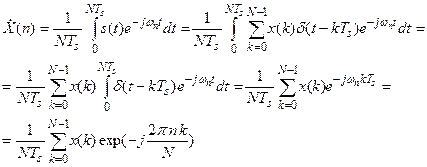(2)
Замечание: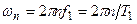 
; 
;
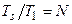Таким образом, формула для вычисления комплексных амплитуд гармоник представляет собой линейную комбинацию отсчетов сигнала.
В выражении (2) реальный масштаб времени фигурирует только в множителе 1/T перед оператором суммирования. При рассмотрении дискретных последовательностей обычно оперируют номерами отсчетов и спектральных гармоник без привязки к действительному масштабу времени и частоты. Поэтому множитель 1/Т из (5.2) удаляют, то есть считают частоту дискретизации равной единице. Удаляют обычно и множитель 1/N (об этом см. замечание ниже). Получившееся выражение называется дискретным преобразованием Фурье (ДПФ; английский термин — Discrete Fourier Transform, DFT):
|
|
|
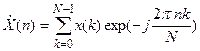(3)
Существует и обратное дискретное преобразование Фурье. Переход от дискретного спектра к временным отсчетам сигнала выражается следующей формулой:
(4)
Это выражение отличается от формулы прямого ДПФ (5.3) лишь знаком в показателе комплексной экспоненты и наличием множителя 1/N перед оператором суммирования.
ЗАМЕЧАНИЕ -----------------------------------------------------------------------------------
В размещении множителя 1/N в формулах (5.3) и (5.4) нет полного единства. В большинстве источников, среди которых [1, 4, 8], а также в математических пакетах компьютерных программ (в том числе и в MATLAB) этот множитель фигурирует в формуле обратного ДПФ (5.4) (этот вариант принят и в данной книге). В то же время в учебнике [2] этот множитель включен в формулу прямого ДПФ (5.3).
Многомерное дискретное преобразование Фурье
Двумерный дискретный ряд Фурье можно представить в виде
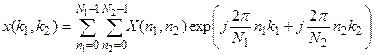
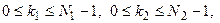
где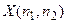 
- коэффициенты ряда Фурье,
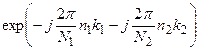- комплексная синусоида, прямоугольно-периодичная с горизонтальным N1 и вертикальным N2 периодом.
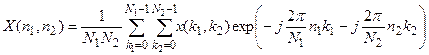
Свойства дискретного преобразования Фурье
В целом свойства ДПФ аналогичны свойствам непрерывного преобразования Фурье, однако дискретный характер анализируемого сигнала привносит некоторую специфику.
Линейность
Из формулы (3) очевидно, что ДПФ является линейным, то есть если последовательностям {x(k)} и {y(k)} с одним и тем же периодом N соответствуют наборы гармоник Х(п) и Y(n), то последовательности {ax(k) + by(k)} будет соответствовать спектр аХ(п)+ bY(n).
Задержка(смещение) функции
Если задержать исходную последовательность на один такт (y(k) = x(k-1)), то, согласно (3), спектр необходимо умножить на ехр(-j2πп/N):
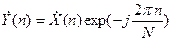
Поскольку мы считаем последовательность {x(k)} периодической, рассматриваемый здесь сдвиг является циклическим: y(0) = х(-1) = x(N - 1).
|
|
|
|
|
|
