 |
Теорема о дискретном равномерном представлении непрерывного сигнала
|
|
|
|
Математически процесс определения значения сигнала в указанной точке описывается следующим выражением
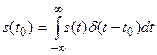
т.к. называемое фильтрующее свойство дельта-функции.
Аппаратно реализуется устройством выборки хранения (УВХ) аналого-цифрового преобразователя (АЦП).
Рисунок УВХ
Базовая операция для превращения непрерывного сигнала в дискретную форму - дискретизация.
Результатом процесса дискретизации является сигнал с амплитудно-импульсной модуляцией.
Рисунок Представление сигнала в дискретной форме – АИМ
Такое название возникло потому, что выходной сигнал УВХ можно описать как последовательность импульсов с амплитудами сигнала в момент выборок.
Исходный непрерывный сигнал можно восстановить из АИМ путем прохождения последнего через восстанавливающий фильтр, при определенных ограничениях, которые формулируются в теореме о равномерном дискретном представлении (теорема Шеннона-Котельникова, критерий Найквиста).
Сигнал с ограниченной полосой, не имеющий спектральных составляющих с частотами, которые превышают 
, однозначно определяется значениями, выбранными через равные промежутки времени
иначе
Это утверждение доказывается строго, но вначале его можно пояснить простым примером
Рисунок
Критерий выбора частоты дискретизации с учетом эффекта наложения
Практический критерий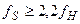 
Компактный \ некомпактный спектр.
Для любого ограниченного во времени сигнала, спектр неограничен (хотя может быть весьма мал выше 
). Для исключения перекрытия спектров производится удаление спектральных составляющих сигнала (предварительная фильтрация сигнала) с частотой выше , т.е. процесс дискретизации всегда вносит некоторые искажения, величина которых определяется отношением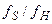 
.
|
|
|
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О ДИСКРЕТНОМ ПРЕДСТАВЛЕНИИ (Столлингс)
Теорему о дискретном представлении можно сформулировать следующим образом. Если
x(t) — сигнал с ограниченной полосой fh,
p(t) — выборочный сигнал, состоящий из импульсов, взятых через интервал 
,где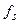 
— частота дискретизации,
xs(t) = x(t)p(t) — дискретный сигнал,
то сигнал x(t) можно восстановить непосредственно из сигнала xs(t) тогда и только тогда, когда fs>2fh.
Доказательство
Поскольку сигнал p(t) состоит из равномерной последовательности импульсов, то он является периодическим сигналом и может быть представлен в виде ряда Фурье:
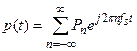
Получаем
Рассмотрим теперь Фурье-образ функции 
:
Подставляя выражение для , имеем
После упрощения получаем
Исходя из определения преобразования Фурье, можем записать следующее:
,
где 
— Фурье-образ функции x(t).
Подставив это в предыдущую формулу, получим
.
Последняя формула имеет интересную интерпретацию, представленную на рис. 6.22, где мы предполагали, не нарушая общности, что полоса сигнала x(t) лежит в диапазоне от 0 до fh. Спектр сигнала xs(t) состоит из спектра сигнала x(t) и спектра, который получается из спектра сигнала x(t) при переносе каждой гармоники на несущую частоту. Каждый из перенесенных спектров умножается на соответствующий коэффициент ряда Фурье для p(t).
Рис. 6.22. Иллюстрация к теореме о дискретном представлении(дорисовать спектр периодически повторяющихся дельта функций)
Если fs > 2fh, то эти перенесенные спектры не перекрываются, а спектр сигнала x(t) умножается на коэффициент Р0, входящий в Xs(f).
Восстановление спектра исходного сигнала x(t) произойдет при передаче сигнала 
через фильтр который сможет отделить одну из периодически повторяющихся копий спектра исходного сигнала. Обычно выделяется копия лежащая на нулевой частоте.
|
|
|
|
|
|
