 |
БПФ с прореживанием по частоте
|
|
|
|
Формулы прямого и обратного ДПФ и отличаются только знаком в показателе экспоненты и множителем перед суммой. Поэтому можно получить еще один вариант алгоритма БПФ, выполнив преобразования, показанные на схеме рис. 1, в обратном порядке. Этот способ вычислений называется прореживанием по частоте (decimation in frequency, DIF). Покажем, как получить описание этого метода на основе формулы прямого ДПФ.

Разделим исходную последовательность { x(k) } на две следующие друг за другом половины (как и в предыдущем случае, N должно быть четным числом):
 .
.
Из второй суммы можно выделить множитель
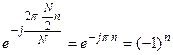
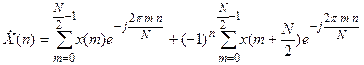
.
Этот множитель равен 1 или -1 в зависимости от четности номера вычисляемого спектрального отсчета n, поэтому дальше рассматриваем четные и нечетные n по отдельности. После выделения множителя ±1 комплексные экспоненты в обеих суммах становятся одинаковыми, поэтому выносим их за скобки, объединяя две суммы:
 ,
,
 .
.
Фигурирующие здесь суммы представляют собой ДПФ суммы и разности половин исходной последовательности, при этом разность перед вычислением ДПФ умножается на комплексные экспоненты exp (-j2πm / N). Каждое из двух используемых здесь ДПФ имеет размерность N/2.
Итак, при прореживании по частоте вычисления организуются следующим образом:
1. Из исходной последовательности { х(k) } длиной N получаются две последовательности { у(m) } и { z(m) } длиной N/2 согласно следующим формулам:
 ,
,
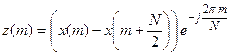 .
.
2. ДПФ последовательности { у(m) } дает спектральные отсчеты с четными номерами, ДПФ последовательности { z(m) } — с нечетными:
 ,
,
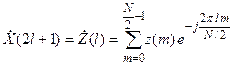 .
.
Все сказанное в предыдущем разделе о возможности деления последовательности на иное, отличное от двух, число частей и об уменьшении числа операций, требуемых для расчетов, относится и к алгоритму с прореживанием по частоте.
|
|
|
Процесс вычисления 8-точечного ДПФ путем разбиения его на два 4-точечных ДПФ с прореживанием по частоте показан на рис. 4.

Рис. 4. Вычисление 8-точечного ДПФ с помощью двух 4-точечных ДПФ путем прореживания по частоте
Поскольку комплексный экспоненциальный множитель в данном алгоритме применяется к результату вычитания двух сигналов, «бабочка» БПФ с прореживанием по частоте имеет несколько иную структурную схему (рис. 5).

Рис. 5. Условное обозначение «бабочки» БПФ с прореживанием по частоте (слева) и ее структурная схема (справа)
ЗАМЕЧАНИЕ
Для получения алгоритма обратного БПФ достаточно поменять в приведенных формулах знак в показателях комплексных экспонент и добавить на выходе (или на входе) деление на два (в более общем случае — на используемый коэффициент прореживания).
Основание алгоритма БПФ
В названиях алгоритмов БПФ можно встретить слово «RADIX» («основание» — в математическом смысле). Следующее после него число обозначает число фрагментов, на которое разбивается сигнал на каждом этапе прореживания (а также минимальный размер «кусочков» входного вектора, который достигается в результате его последовательных разбиений).
В алгоритмах «RADIX-2» размер анализируемой последовательности должен быть равен степени двойки, а ее половинное деление производится вплоть до получения двухэлементных последовательностей. Вычисление их ДПФ не требует операций умножения — два спектральных отсчета представляют собой сумму и разность отсчетов временных:
 ,
,
 .
.
В алгоритмах «RADIX-4» количество отсчетов сигнала должно быть равно степени четверки, при каждом прореживании сигнал делится на четыре фрагмента, а последней стадией деления являются четырехэлементные последовательности. При вычислении их ДПФ умножение производится только на ±j, а такое умножение сводится к взаимной перестановке вещественной и мнимой частей комплексного числа с изменением знака у одной из них:
|
|
|
 ,
,
 ,
,
 ,
,
 .
.
Использование основания 4 позволяет ощутимо уменьшить число выполняемых умножений. Увеличивая основание БПФ можно снизить количество умножений, обычно не более RADIX-4.
|
|
|


