 |
Тема № 2. Элементы векторной алгебры и аналитической геометрии
|
|
|
|
2.1. Даны вершины треугольной пирамиды 
, 
. Найти:
1) угол между ребрами 
и 
;
2) площадь грани 
;
3) объем пирамиды 
;
4) длину высоты, опущенной из вершины S на грань АВС;
5) уравнение высоты, опущенной из вершины S на грань АВС.
Тема № 3. Предел и производная функции одной переменной
3.1. С помощью методов дифференциального исчисления исследовать и построить график функции 
Тема № 4. Интегральное исчисление функции одной переменной
4.1.Найти интеграл 
.
4.2.Найти интеграл 
.
4.3. Найти интеграл 
.
4.4. Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
, 
.
Тема № 5. Дифференциальное исчисление функции нескольких переменных.
5.1. Найти дифференциал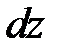 
функции 
.
5.2. Показать, что функция 
удовлетворяет уравнению 
.
Краткие теоретические сведения для выполнения
Контрольной работы
И решение типовых задач
Тема 1 Элементы линейной алгебры
Матрицы и действия над ними
Прямоугольная таблица чисел вида
называется матрицей размера m ´ n; здесь m – число строк, n – число столбцов.
Числа 
(i = 1,2,…, m; j = 1,2,…, n) составляющие матрицу, называются ее элементами. Первый индекс i означает номер строки, второй j – номер столбца.
Если число строк и столбцов матрицы одинаковое 
, то матрица называется квадратной, порядка n.
Квадратная матрица, в которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной, а диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице, называется единичной:
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю. Например:
|
|
|
.
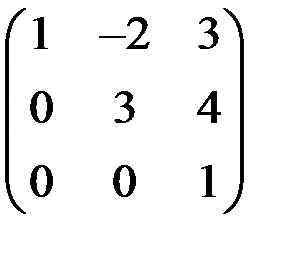Матрица, все элементы которой равны нулю, называется нулевой и обозначается символом О, например 
.
Прямоугольная матрица, в которой каждая строка заменена столбцом с тем же номером, называется транспонированной по отношению к данной матрице, обозначается 
. Например, если 
, то 
.
Очевидно, что 
.
Действия над матрицами
Две матрицы одинакового размера называются равными, если их соответствующие элементы равны.
А = В, если = 
(i = 1,2,…, m; j = 1,2,…, n).
Суммой двух матриц одинакового размера называется матрица того же размера, все элементы которой равны суммам соответствующих элементов слагаемых матриц.
А + В = С, если + = 
(i = 1,2,…, m; j = 1,2,…, n).
Пример 1
.
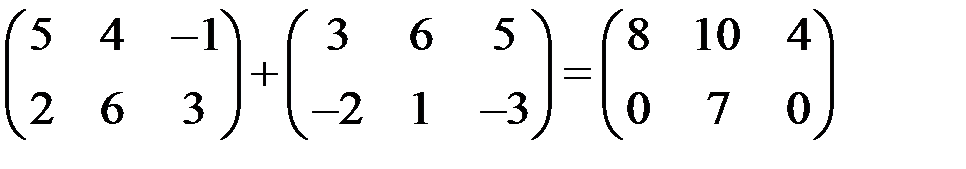Произведением матрицы А на число α называется матрица αА или А α, все элементы которой равны соответствующим элементам матрицы А, умноженным на α.
Пример 2
Матрица 
называется противоположной матрице А.
Умножение матриц.
Пусть дана матрица А размера m ´ n и матрица В размера n ´ p.
Для двух матриц А и В, у которых число столбцов первой матрицы равно числу строк второй матрицы, определено понятие произведения матрицы А на В следующим образом:
С = А · В, где С есть матрица размера m ´ p,
,
если 
, где (i = 1,2,…, m; j = 1,2,…, p).
Из определения вытекает следующее правило умножения матриц: чтобы получить элемент, стоящий в i -той строке и j -том столбце произведения двух матриц, нужно элементы i -той строки первой матрицы умножить на соответствующие элементы j –го столбца второй и полученные произведения сложить.
Таким образом, чтобы составить первую строку матрицы С нужно перемножить первую строку матрицы А поочередно на все столбцы В; чтобы получить вторую строку произведения С, нужно вторую строку А перемножить последовательно на все столбцы В и т.д.
Пример 3 
Произведение двух матриц НЕ подчиняется переместительному (коммутативному) закону
|
|
|
,
в чем можно убедиться на примерах. Кроме того, если произведение АВ определено, то ВА может не иметь смысла.
В частных случаях, когда 
матрицы называются перестановочными.
Легко доказать, что единичная матрица Е перестановочна с любой квадратной матрицей А того же порядка, причем
А Е = Е А = А.
Таким образом, единичная матрица играет роль единицы при умножении.
Пример 4
Найти значение матричного многочлена 
, если 
, 
, 
.
Решение
.
|
|
|
